新闻分类：多分类问题

本文章参考《python深度学习》

新闻分类：多分类问题

新闻主题有多个类别，所 这是多分类（multiclass classification）问题的一个例子。因为每个数据点只能划分到一个类别， 所以更具体地说，这是单标签、多分类（single-label, multiclass classification）问题的一个例 子。如果每个数据点可以划分到多个类别（主题），那它就是一个多标签、多分类（multilabel, multiclass classification）问题。

这篇文章会构建一个网络，将路透社新闻划分为46个互斥的主题。

路透社数据集

它包含许多短新闻及其对应的主题，由路透社在1986 年发布。它是一个简单的、广泛使用的文本分类数据集。它包括46 个不同的主题：某些主题的样本更多， 但训练集中每个主题都有至少 10 个样本。 与 IMDB和MNIST 类似，路透社数据集也内置为Keras 的一部分。

from keras.datasets import reuters

(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)

print(train_data[10])
[1, 245, 273, 207, 156, 53, 74, 160, 26, 14, 46, 296, 26, 39, 74, 2979, 3554, 14, 46, 4689, 4329, 86, 61, 3499, 4795, 14, 61, 451, 4329, 17, 12]

与IMDB评论一样，每个样本都是一个整数列表（表示单词索引）,甚至将索引解码为新闻文本的方式都一样，只不过要使用reuters.get_word_index()。

我们有 8982 个训练样本和 2246 个测试样本。

>>> len(train_data) 
8982 
>>> len(test_data) 
2246

然后是将数据向量化，可以使用与电影评论中相同的vectorize_sequences函数；不过这里的标签向量化方式不同，需要使用one_hot编码，也叫分类编码（categorical encoding）。

在这个例子中，标签的one-hot编码就是将每个标签表示为全零向量， 只有标签索引对应的元素为 1。

可以使用以下代码自己实现这一过程：

import numpy as np

def to_one_hot(labels, dimension=46):
    results = np.zeros((len(labels), dimension))
    for i, label in enumerate(labels):
        results[i, label] = 1.
    return results

one_hot_train_labels = to_one_hot(train_labels)
one_hot_test_labels = to_one_hot(test_labels)

实际上，to_one_hot函数与vectorize_sequences函数完全一致（仅dimension的默认参数值不同），

我在电影评论的文章中就有提及，keras.utils.to_categorical()方法具有类似vectorize_sequences的功能，但是其只能接受一个向量作为参数，无法接受二维数组（2D张量）。但是这里，标签就是一维张量，所以完全可以使用Keras的内置方法。

完整地数据处理过程

from keras.datasets import reuters
from keras.utils import to_categorical
import numpy as np

(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)


def vectorize_sequences(labels, dimension=10000):
    results = np.zeros((len(labels), dimension))
    for i, label in enumerate(labels):
        results[i, label] = 1.
    return results


# 将训练数据向量化
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
# 将训练标签向量化
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)

构建网络

​ 这个主题分类问题与前面的电影评论分类问题类似，两个例子都是试图对简短的文本片段进行分类。但这个问题有一个新的约束条件：输出类别的数量从2 个变为46 个。输出空间的维 度要大得多。

​ 对于前面用过的 Dense 层的堆叠，每层只能访问上一层输出的信息。如果某一层丢失了与 分类问题相关的一些信息，那么这些信息无法被后面的层找回，也就是说，每一层都可能成为 信息瓶颈。上一个例子使用了16 维的中间层，但对这个例子来说16 维空间可能太小了，无法 学会区分 46 个不同的类别。这种维度较小的层可能成为信息瓶颈，永久地丢失相关信息。

​ 出于这个原因，下面将使用维度更大的层，包含 64 个单元。

from keras import models
from keras import layers

# 模型定义
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

# 编译模型
model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['acc'])

关于这个架构还应该注意另外两点。

1. 网络的最后一层是大小为46 的 Dense 层。这意味着，对于每个输入样本，网络都会输出一个 46 维向量。这个向量的每个元素（即每个维度）代表不同的输出类别。
2. 最后一层使用了softmax 激活。你在MNIST例子中见过这种用法。网络将输出在46 个不同输出类别上的概率分布——对于每一个输入样本，网络都会输出一个 46 维向量， 其中 output[i] 是样本属于第 i 个类别的概率。46 个概率的总和为 1。

对于这个例子，最好的损失函数是 categorical_crossentropy（分类交叉熵）。它用于衡量两个概率分布之间的距离，这里两个概率分布分别是网络输出的概率分布和标签的真实分布。通过将这两个分布的距离最小化，训练网络可使输出结果尽可能接近真实标签。

验证方法

import matplotlib.pylab as plt

# 留出验证集
x_val = x_train[:1000]
partial_x_train = x_train[1000:]

y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]

# 训练模型
history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
                    validation_data=(x_val, y_val))
history_dict = history.history
loss_values = history_dict["loss"]  # 训练数据的损失
acc_values = history_dict["acc"]  # 训练数据的准确率
val_loss_values = history_dict["val_loss"]  # 验证数据的损失
val_acc_values = history_dict["val_acc"]   # 验证数据的准确率

epochs = range(1, len(loss_values) + 1)

# 绘制训练损失和验证损失
plt.plot(epochs, loss_values, 'bo', label="Training loss")
plt.plot(epochs, val_loss_values, 'b', label="Validation loss")
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

# 清空图像
plt.clf()
# 绘制训练精度和验证精度
plt.plot(epochs, acc_values, 'bo', label="Training acc")
plt.plot(epochs, val_acc_values, 'b', label="Validation acc")
plt.title("Training and validation accuracy")
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend()
plt.show()

下面是训练过程中的训练损失和验证损失、训练精度和验证精度图：

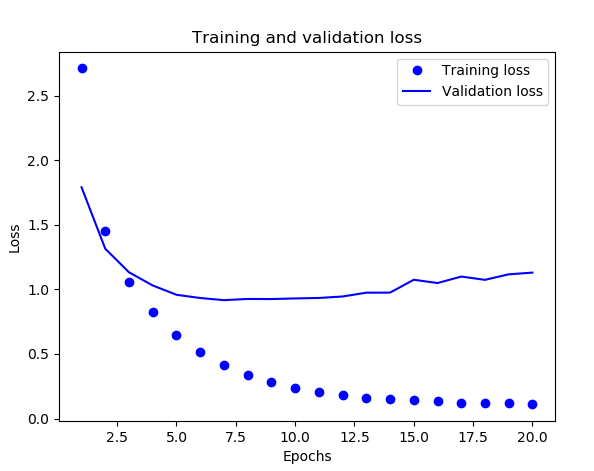
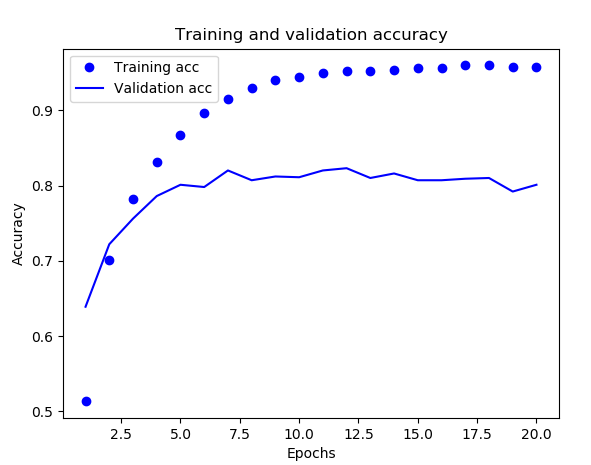
虽然在《Python深度学习》中的例子，网络在训练9轮后开始过拟合，但是这里我们的实际情况(可能因为不同的机器配置或什么原因会有一些微小的差别)大概是在7轮，所以如果我们训练7轮后就停止训练，可以简单地得到近似78%的准确率。

测试与预测

当训练好网络之后，我们可以先使用测试集来测试准确度

results = model.evaluate(x_test, one_hot_test_labels)
print(results)

[0.9962977889596832, 0.7849510312080383]

第一个是测试集的损失值，第二个是测试集的准确率。

当测试的准确率达到我们的需求时，我们可以用这一网络来预测新数据

predictions = model.predict(x_test)
# predictions 中的每个元素都是长度为 46 的向量
print(predictions[0].shape)
(46,)
# 这个向量的所有元素总和为 1（这里出现过不等于1的情况，例如0.9999994）
print(np.sum(predictions[0]))
1.0
# 最大的元素就是预测类别，即概率最大的类别(书上的例子这里结果是4)
print(np.argmax(predictions[0]))
3

处理标签和损失的另一种方法

除了将标签转化为ont-hot编码，还可以直接将其转化为整数张量（实际上就是变为numpy数组，本身还是一个”列表”）

y_train = np.array(train_labels) 
y_test = np.array(test_labels)

对于这种编码方法，唯一需要改变的是损失函数的选择。对于上面使用的损失函数categorical_crossentropy，标签应该遵循分类编码。对于整数标签，你应该使用 sparse_categorical_crossentropy。

model.compile(optimizer='rmsprop',               
              loss='sparse_categorical_crossentropy',               
              metrics=['acc'])

这个新的损失函数在数学上与 categorical_crossentropy 完全相同，二者只是接口不同。

中间层维度足够大的重要性

前面提到，最终输出是46 维的，因此中间层的隐藏单元个数不应该比46 小太多。现在来看一下，如果中间层的维度远远小于 46（比如 4 维），造成了信息瓶颈，那么会发生什么？

# 具有信息瓶颈的模型
model = models.Sequential() 
model.add(layers.Dense(64, activation='relu', input_shape=(10000,))) model.add(layers.Dense(4, activation='relu')) 
model.add(layers.Dense(46, activation='softmax')) 

model.compile(optimizer='rmsprop',               
              loss='categorical_crossentropy',               
              metrics=['accuracy']) 
model.fit(partial_x_train,           
          partial_y_train,           
          epochs=20,           
          batch_size=128,           
          validation_data=(x_val, y_val))

现在网络的验证精度最大约为 71%，比前面下降了一些。导致这一下降的主要原因在于，你试图将大量信息（这些信息足够恢复46 个类别的分割超平面）压缩到维度很小的中间空间。网络能够将大部分必要信息塞入这个四维表示中，但并不是全部信息。

改进与总结

改进（应该说是试验）

1. 尝试使用更多或更少的隐藏单元，比如 32 个、128 个等。
2. 前面使用了两个隐藏层，现在尝试使用一个或三个隐藏层。

只有不断试验才能改进。

总结

1. 如果要对 N 个类别的数据点进行分类，网络的最后一层应该是大小为 N 的 Dense 层。

2. 对于单标签、多分类问题，网络的最后一层应该使用 softmax 激活，这样可以输出在 N 个输出类别上的概率分布。

3. 这种问题的损失函数几乎总是应该使用分类交叉熵。它将网络输出的概率分布与目标的真实分布之间的距离最小化。

4. 处理多分类问题的标签有两种方法：

   （1）、通过分类编码（也叫one-hot 编码）对标签进行编码，然后使用categorical_ crossentropy 作为损失函数。

   （2）、将标签编码为整数，然后使用 sparse_categorical_crossentropy 损失函数。

5. 如果你需要将数据划分到许多类别中，应该避免使用太小的中间层，以免在网络中造成 信息瓶颈。