理解循环神经网络

发表于 | 分类于

本文章参考《python深度学习》

理解循环神经网络

密集连接网络和卷积神经网络都有一个主要特点，就是没有记忆，它们单独处理每个输入，在输入与输入之间没有保存任何状态。对于这 样的网络，要想处理数据点的序列或时间序列，你需要向网络同时展示整个序列，即将序列转换成单个数据点。例如，你在IMDB 示例中就是这么做的：将全部电影评论转换为一个大向量， 然后一次性处理。这种网络叫作前馈网络（feedforward network）。

与此相反，当你在阅读这个句子时，你是一个词一个词地阅读（或者说，眼睛一次扫视一 次扫视地阅读），同时会记住之前的内容。这让你能够动态理解这个句子所传达的含义。生物智能以渐进的方式处理信息，同时保存一个关于所处理内容的内部模型，这个模型是根据过去的信息构建的，并随着新信息的进入而不断更新。

循环神经网络（RNN，recurrent neural network）采用同样的原理，不过是一个极其简化的版本：它处理序列的方式是，遍历所有序列元素，并保存一个状态（state），其中包含与已查看内容相关的信息。实际上，RNN 是一类具有内部环的神经网络。

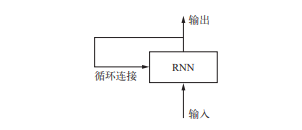
在处理两个不同的独立序列（比如两条不同的IMDB 评论）之间，RNN 状态会被重置，因此，你仍可以将一个序列看作单个数据点，即网络的单个输入。真正改变的是，数据点不再是在单个步骤中进行处理， 相反，网络内部会对序列元素进行遍历。

在介绍使用Numpy模拟实现RNN的前向传递之前先补充一些Numpy中张量点积的知识

np.dot 张量点积

  • 当两个操作数均为矩阵时，进行矩阵乘积运算

    两个矩阵相乘条件：前面矩阵的列数等于后面矩阵的行数

  • 当两个操作数均为向量时，进行向量点积运算

    两个向量中的元素逐元素相乘，并求和，结果是一个标量

    两个向量点积的条件：两个向量元素个数相同

  • 当操作数为向量和矩阵：

  1. np.dot(x, y)，左面矩阵x、右面向量y

    返回值是一个向量，向量元素个数与矩阵x的行数相同，且向量的每个元素是y和x的每一行之间的点积；相当于每次拿出矩阵x的一行，与y做向量点积

    所以要求矩阵x的每行元素的个数(列数)与向量y的元素个数相同；

  2. np.dot(y, x)左面向量y、右面矩阵x：(此种情况很少有资料介绍，事实上也是可以运算的)

    返回值是一个向量，向量元素个数与矩阵x的列数相同，且向量的每个元素是y和x每一列之间的点积；相当于每次拿出矩阵x的一列，与y做向量点积

    所以要求矩阵x的每列元素的个数(行数)与向量y的元素个数相同。

使用Numpy模拟实现RNN的前向传递

为了将环（loop）和状态的概念解释清楚，我们用 Numpy 来实现一个简单RNN的前向传递。

这个 RNN的输入是一个张量序列，我们将其编码成大小为 (time_steps, input_features) 的二维张量。它对时间步（time_step）进行遍历，在每个时间步，它考虑 t 时刻的当前状态与 t 时刻的输入［形状为 (input_ features,)］，对二者计算得到 t 时刻的输出。然后，我们将下一个时间步的状态设置为上一个时间步的输出。对于第一个时间步，上一个时间步的输出没有定义，所以它没有当前状态。因此，你需要将状态初始化为一个全零向量，这叫作网络的初始状态（initial state）。

1
2
3
4
5
6
7
# t时刻的状态
state_t = 0
# 对序列元素进行遍历
for input_t in input_sequence:
    output_t = f(input_t, state_t)
    # 前一次输出变成下一次迭代的状态
    state_t = output_t

你可以给出具体的函数 f：从输入和状态到输出的变换，其参数包括两个矩阵（W 和 U） 和一个偏置向量。它类似于前馈网络中密集连接层所做的变换。

1
2
3
4
state_t = 0
for input_t in input_sequence:
    output_t = activation(dot(W, input_t)+dot(U, state_t)+b)
    state_t = output_t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np

# 输入序列的时间步数
time_steps = 100
# 输入特征空间的维度
input_features = 32
# 输出特征空间的维度
output_features = 64

# 输入数据：随机噪声，仅作为示例
inputs = np.random.random((time_steps, input_features))
# 初始状态：全零向量
state_t = np.zeros((output_features,))

# 创建随机的权重矩阵
W = np.random.random((output_features, input_features))
U = np.random.random((output_features, output_features))
b = np.random.random((output_features, ))


successive_outputs = []
# input_t是形状为(input_features,)的向量
for input_t in inputs:
    # 正切，将值的范围限制到[-1, 1]之间
    output_t = np.tanh(np.dot(W, input_t)+np.dot(U, state_t)+b)

    successive_outputs.append(output_t)
    # 更新网络的状态，用于下一个时间步
    state_t = output_t

print(successive_outputs)
final_output_sequence = np.stack(successive_outputs, axis=0)
# 最终输出是一个形状为 (timesteps, output_features) 的二维张量
print(final_output_sequence)

总之，RNN 是一个 for 循环，它重复使用循环前一次迭代的计算结果。当然，你可以构建许多不同的RNN，它们都满足上述定义。这个例子只是最简单的RNN表述之一。

RNN 的特征在于其时间步函数，比如前面例子中的这个函数:

output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)

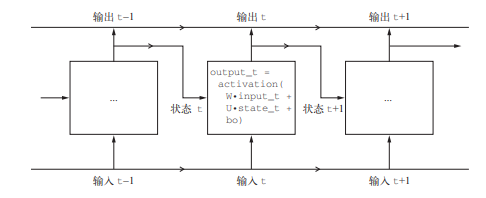
注意：本例中，最终输出是一个形状为 (time_steps, output_features) 的二维张量，其中每个时间步是循环在 t 时刻的输出。输出张量中的每个时间步 t 包含输入序列中时间步 0~t 的信息，即关于全部过去的信息。因此，在多数情况下，你并不需要这个所有输出组成的序列，你只需要最后一个输出（循环结束时的 output_t），因为它已经包含了整个序列的信息。

Keras中的循环层

上面 Numpy 的简单实现，对应一个实际的 Keras 层，即 SimpleRNN 层。

from keras.layers import SimpleRNN

二者有一点小小的区别：SimpleRNN 层能够像其他 Keras 层一样处理序列批量，而不是像 Numpy 示例那样只能处理单个序列。因此，它接收形状为 (batch_size, time_steps, input_features) 的输入，而不是 (time_steps, input_features)。

与 Keras 中的所有循环层一样，SimpleRNN 可以在两种不同的模式下运行：

  1. 返回每个时间步连续输出的完整序列，即形状为 (batch_size, time_steps, output_features) 的三维张量；

  2. 只返回每个输入序列的最终输出，即形状为 (batch_size, output_ features) 的二维张量。这两种模式由 return_sequences 这个构造函数参数来控制。

我们来看一个使用 SimpleRNN 的例子，它只返回最后一个时间步的输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from keras.models import Sequential
from keras.layers import Embedding, SimpleRNN

model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32))
model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, 32)                2080      
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0
_________________________________________________________________

下面这个例子返回完整的状态序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, None, 32)          2080      
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0

为了提高网络的表示能力，将多个循环层逐个堆叠有时也是很有用的。在这种情况下，你需要让所有中间层都返回完整的输出序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
# 最后一层仅返回最终输出
model.add(SimpleRNN(32))
model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_2 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_3 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_4 (SimpleRNN)     (None, 32)                2080      
=================================================================
Total params: 328,320
Trainable params: 328,320
Non-trainable params: 0

将模型应用于IMDB电影评论分类

首先，对数据进行预处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from keras.datasets import imdb
from keras.preprocessing import sequence


max_features = 10000
max_len = 500
print('Loading data...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
print(len(input_train), 'train sequences')
print(len(input_test), 'test sequences')

print('Pad sequences (samples x time)')
input_train = sequence.pad_sequences(input_train, maxlen=max_len)
input_test = sequence.pad_sequences(input_test, maxlen=max_len)
print('input_train shape:', input_train.shape)
print('input_test shape:', input_test.shape)

使用一个Embedding层和一个SimpleRNN层来训练一个简单的循环网络

1
2
3
4
5
6
7
8
9
from keras.layers import Dense

model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train, epochs=10, batch_size=128, validation_split=0.2)

接下来显示训练和验证的损失和精度(代码略，前面已经出现过N次了)

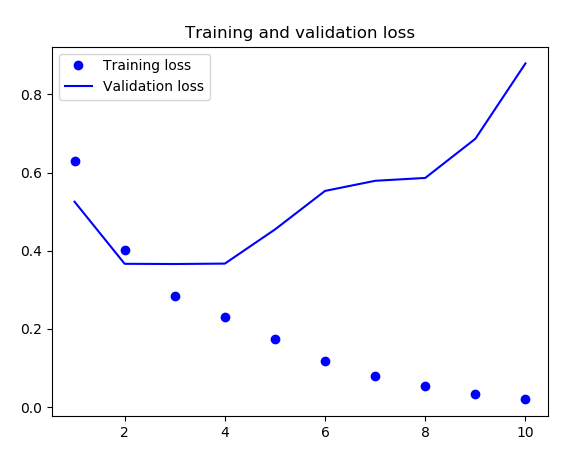
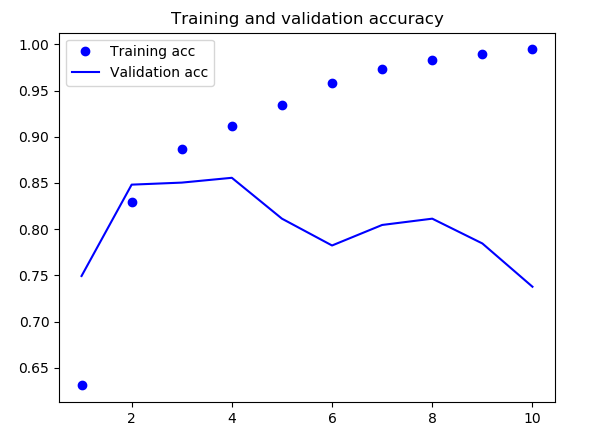
可以看到这里第4轮左右验证损失降到最低，验证准确率大概在85%，然而我们前面在处理这个数据集的第一个简单方法得到的测试精度是88%。

问题的部分原因在于， 输入只考虑了前 500 个单词，而不是整个序列，因此，RNN 获得的信息比前面的基准模型更少。 另一部分原因在于，SimpleRNN 不擅长处理长序列，比如文本。 其他类型的循环层的表现要好得多。

高级循环神经网络

长期依赖问题

有时候候，我们仅仅需要知道先前的信息来执行当前的任务。例如，我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词，我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN 可以学会使用先前的信息。

有时候，我们仅仅需要知道先前的信息来执行当前的任务。例如，我们有一个语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词，我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN 可以学会使用先前的信息。

但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France… I speak fluent French”最后的词。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的 France 的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。

SimpleRNN 的最大问题是， 在时刻 t，理论上来说，它应该能够记住许多时间步之前见过的信息，但实际上它是不可能学到这种长期依赖的。其原因在于梯度消失问题（vanishing gradient problem），这一效应类似于在层数较多的非循环网络（即前馈网络）中观察到的效应：随着层数的增加，网络最终变得无法训练。

Hochreiter、Schmidhuber 和 Bengio 在 20 世纪 90 年代初研究了这一效应的理论原因

参考论文：

BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult [C]//IEEE Transactions on Neural Networks, 1994, 5(2): 157-166.

HOCHREITER S, SCHMIDHUBER J. Long short-term memory [J]. Neural Computation, 1997, 9(8): 1735-1780.

LSTM网络

长短期记忆（LSTM，long short-term memory）算法由 Hochreiter 和 Schmidhuber 在 1997 年开发 ，是二人研究梯度消失问题的重要成果。

LSTM 层是 SimpleRNN 层的一种变体，它增加了一种携带信息跨越多个时间步的方法。假设有一条传送带，其运行方向平行于你所处理的序列。序列中的信息可以在任意位置跳上传送带， 然后被传送到更晚的时间步，并在需要时原封不动地跳回来。这实际上就是 LSTM 的原理：它保存信息以便后面使用，从而防止较早期的信号在处理过程中逐渐消失。

为了详细了解LSTM，我们先从 SimpleRNN 单元开始讲起。因为有许多个权重矩阵，所以对单元中的 W 和 U 两个矩阵添加下标字母 o（Wo 和 Uo），表示输出。

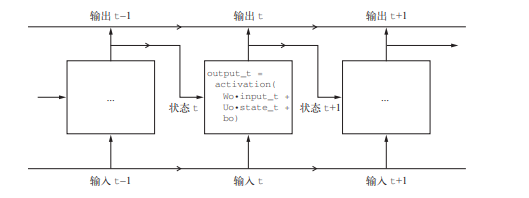
这个图和上面的SimpleRNN图差别仅仅是Wo和Uo

我们向这张图像中添加额外的数据流，其中携带着跨越时间步的信息。它在不同的时间步的值叫作 Ct，其中 C 表示携带（carry）。这些信息将会对单元产生以下影响：它将与输入连接和循环连接进行运算（通过一个密集变换，即与权重矩阵作点积，然后加上一个偏置，再应用 一个激活函数），从而影响传递到下一个时间步的状态（通过一个激活函数和一个乘法运算）。 从概念上来看，携带数据流是一种调节下一个输出和下一个状态的方法。

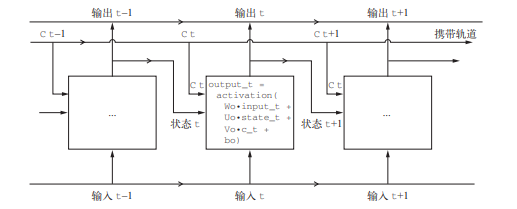
下面来看这一方法的精妙之处，即携带数据流下一个值的计算方法。它涉及三个不同的变换， 这三个变换的形式都和SimpleRNN 单元相同。

1
y = activation(dot(state_t, U) + dot(input_t, W) + b)
1
output_t = activation(dot(state_t, Uo) + dot(input_t, Wo) + dot(C_t, Vo) + bo)

相当于多了一个点积运算

但这三个变换都具有各自的权重矩阵，我们分别用字母 i、j 和 k 作为下标。

Ct的计算方式

1
2
3
4
5
i_t = activation(dot(state_t, Ui) + dot(input_t, Wi) + bi)
f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bf)
k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bk)

c_t+1 = i_t * k_t + c_t * f_t

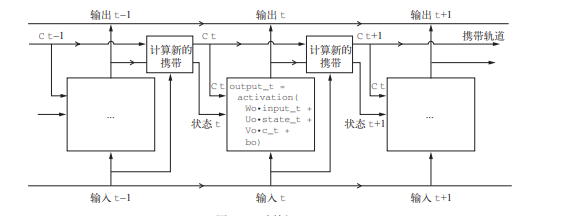
如果要更哲学一点，你还可以解释每个运算的目的。比如你可以说，将 c_t 和 f_t 相乘， 是为了故意遗忘携带数据流中的不相关信息。同时，i_t 和 k_t 都提供关于当前的信息，可以用新信息来更新携带轨道。但归根结底，这些解释并没有多大意义。

因为这些运算的实际效果 是由参数化权重决定的，而权重是以端到端的方式进行学习，每次训练都要从头开始，不可能为某个运算赋予特定的目的。

RNN 单元的类型（如前所述）决定了你的假设空间，即在训练期间搜索良好模型配置的空间，但它不能决定 RNN 单元的作用，那是由单元权重来决定的。同一个单元具有不同的权重，可以实现完全不同的作用。

因此，组成 RNN 单元的运算组合，最好被解释为对搜索的一组约束，而不是一种工程意义上的设计。 对于研究人员来说，这种约束的选择（即如何实现 RNN 单元）似乎最好是留给最优化算法 来完成（比如遗传算法或强化学习过程），而不是让人类工程师来完成。在未来，那将是我们 建网络的方式。

总之，你不需要理解关于 LSTM 单元具体架构的任何内容。作为人类，理解它不应该是你要做的。你只需要记住LSTM 单元的作用：允许过去的信息稍后重新进入，从而解决梯度消失问题。

太喜欢这句总结了，不用了解，哈哈哈~

如果想详细了解LSTM网络究竟了做了什么，可以参考这篇博哥理解LSTM网络，原博客(英文)链接为Understanding-LSTMs。

另外，LSTM还有很多变体，其中比较流行的有Gated Recurrent Unit (GRU)等。

Keras中一个LSTM的具体例子

现在我们来看一个更实际的问题：使用 LSTM 层来创建一个模型，然后在 IMDB 数据上 训练模型。这个网络与前面介绍的 SimpleRNN 网络类似。你只需指定 LSTM 层的输出维度，其他所有参数（有很多）都使用 Keras 默认值。Keras 具有很好的默认值， 无须手动调参，模型通常也能正常运行。

1
2
3
4
5
6
7
8
9
from keras.layers import LSTM


model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train, epochs=10, batch_size=128, validation_split=0.2)

这一次，验证精度达到了89%。还不错，肯定比 SimpleRNN 网络好多了，这主要是因为 LSTM 受梯度消失问题的影响要小得多。这个结果也比上面讲的全连接网络略好，虽然使用的数据量比全连接模型要少。此处在 500 个时间步之后将序列截断，而在全连接网络读取整个序列。

但对于一种计算量如此之大的方法而言，这个结果也说不上是突破性的。为什么 LSTM 不 能表现得更好？

一个原因是你没有花力气来调节超参数，比如嵌入维度或 LSTM 输出维度。

另一个原因可能是缺少正则化。

但说实话，主要原因在于，适用于评论分析全局的长期性结构（这正是 LSTM 所擅长的），对情感分析问题帮助不大。对于这样的基本问题，观察每条评论中出现了哪些词及其出现频率就可以很好地解决。这也正是第一个全连接方法的做法。但还有更加困难的自然语言处理问题，特别是问答和机器翻译，这时 LSTM 的优势就明显了。

总结

本文共讲了以下内容：

  • 循环神经网络（RNN）的概念及其工作原理。
  • 长短期记忆（LSTM）是什么，为什么它在长序列上的效果要好于普通 RNN。
  • 如何使用 Keras 的 RNN 层来处理序列数据。