手动推导BP网络
本文章转载自CSDN
原作者:ZJE_ANDY
原文链接:https://blog.csdn.net/u014453898/article/details/88607537
BP网络神经元
从神经网络中拿出一个神经元j分析:
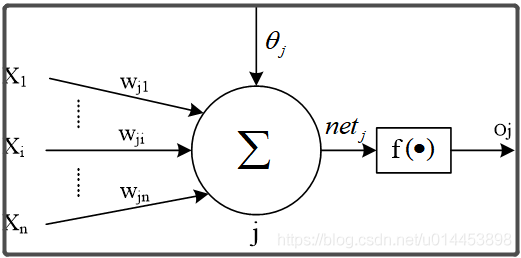

一:BP算法第一阶段:输入信息的正向传播阶段
为了理论一致性,这里先不假设激活函数为Sigmoid函数,而是用 f1()表示隐藏层的激活函数,f2()表示输出层激活函数:
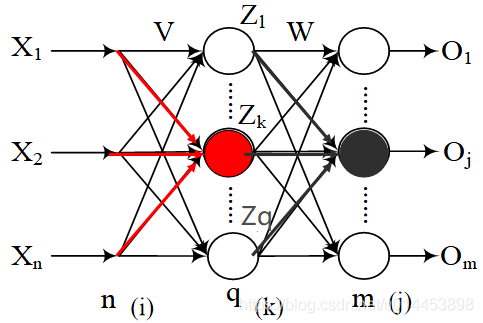
隐藏层结点的输出:
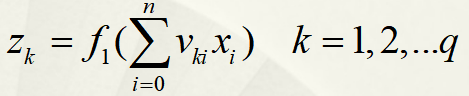
其中Vki为 Xi 到 Zk的权重。可以见到Z的值为 各个输入乘对应权重之和再经过激活函数 输出的值。
输出层结点的输出:
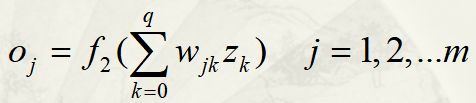
其中Wjk为 Zk 到 Oj 的权重。
二:BP算法第二阶段:误差反向传播阶段
1、由于训练样本中,出现异常数据(即噪音数据)是常见的事情,因此,如果因为噪音数据而调整网络参数的话,就会影响网络的准确率。
因此在神经网络中,批处理是经常被用来解决噪音数据的方法,意思是并非一个输入样本[x1,x2....xn]输入网络后,马上调整网络的权值,而是当输入一组样本(例如一组有p个样本)后,才开始调整权值。
2、到误差反传阶段,我们需要定义损失函数 :
若数据集的期望输出是 Y,而网络的输出是 O,则误差当然为 (Y - O):
但一般我们不会只写成这种形式,而是: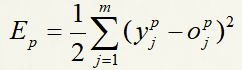
表示第p个样本的误差。乘了个1/2 和 加了个平方是因为,后面的操作会对损失函数进行求导,这样可以方便计算。
同理,一组样本的误差为:
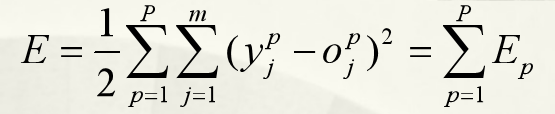
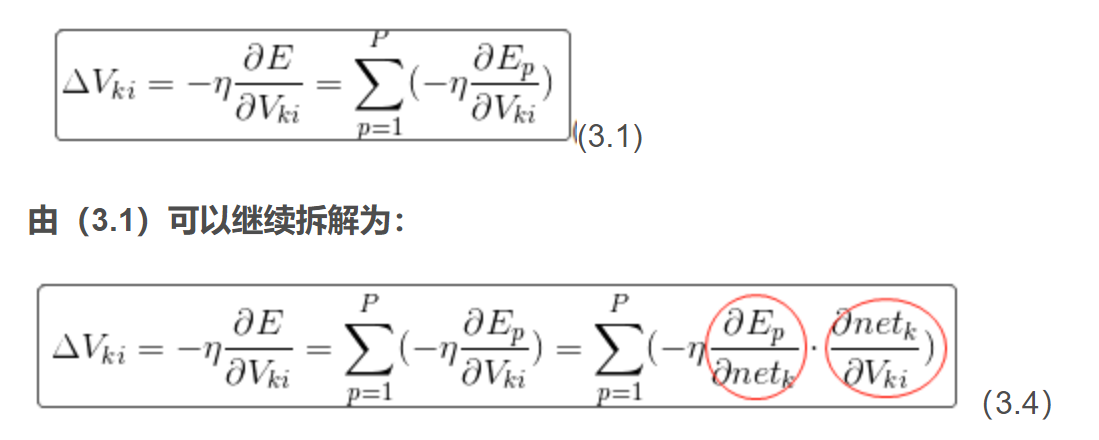
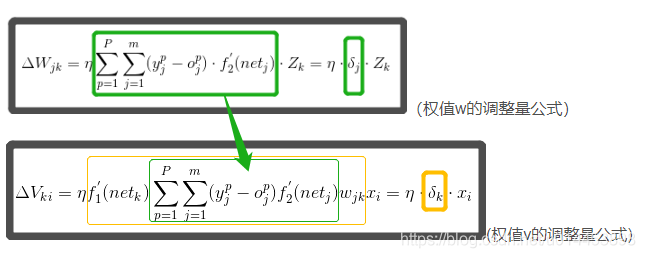
3、有了损失函数之后,我们要求哪个参数的变化量,就对损失函数求该参数的导:(如Wjk)
下面公式是基于梯度下降法来做的,往着负梯度方向就是使损失函数E达到最小值的方向。(为学习率)

(2)式变形可得(3)式—–>详情参考独立神经元的图:
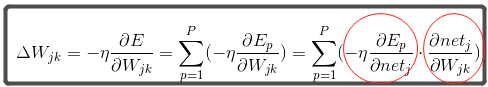
(3)式中红圈处可以继续拆分:
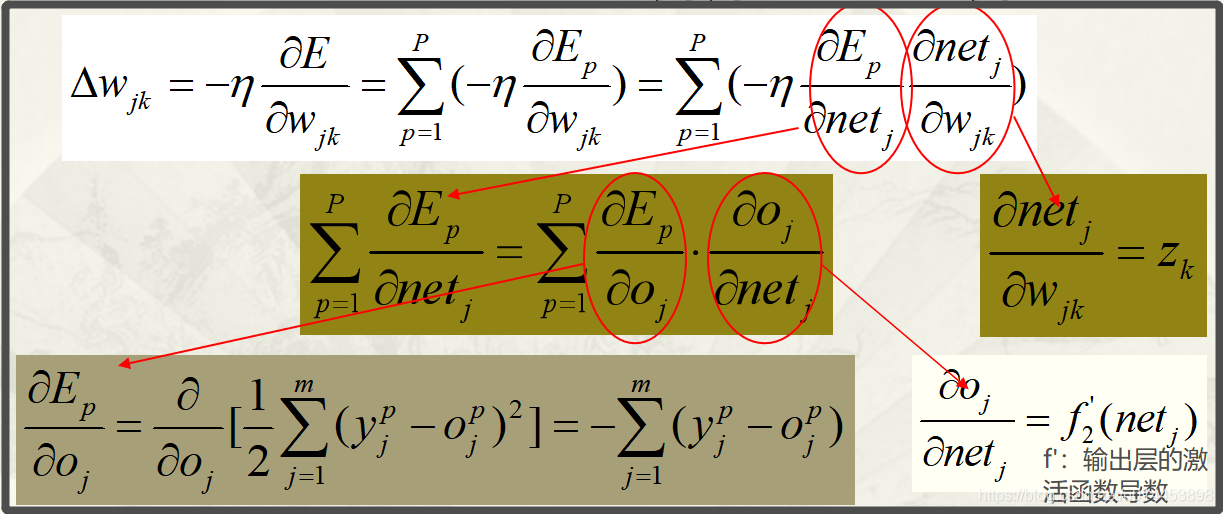
最后得输出层的权值调整量:

到此,隐藏层Z到输出层O之间的各个权值W的调整量就出来了。(如黄色圈)
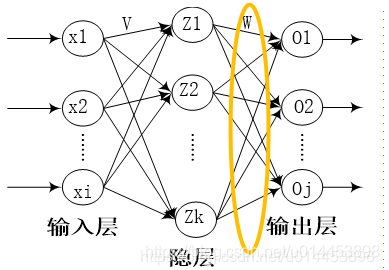
接下来,我们继续反向传导,求出输入层X到隐藏层Z之间的权值V的调整量。
三:求输入层X到隐藏层Z之间的权值V的调整量
依然从损失函数E下手:
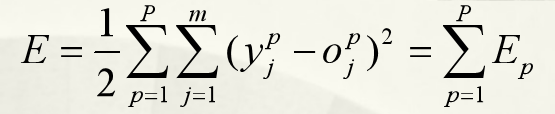
同样用梯度下降的方法,所以(例如)权值Vki的调整量为:
红色圈可以继续拆分:
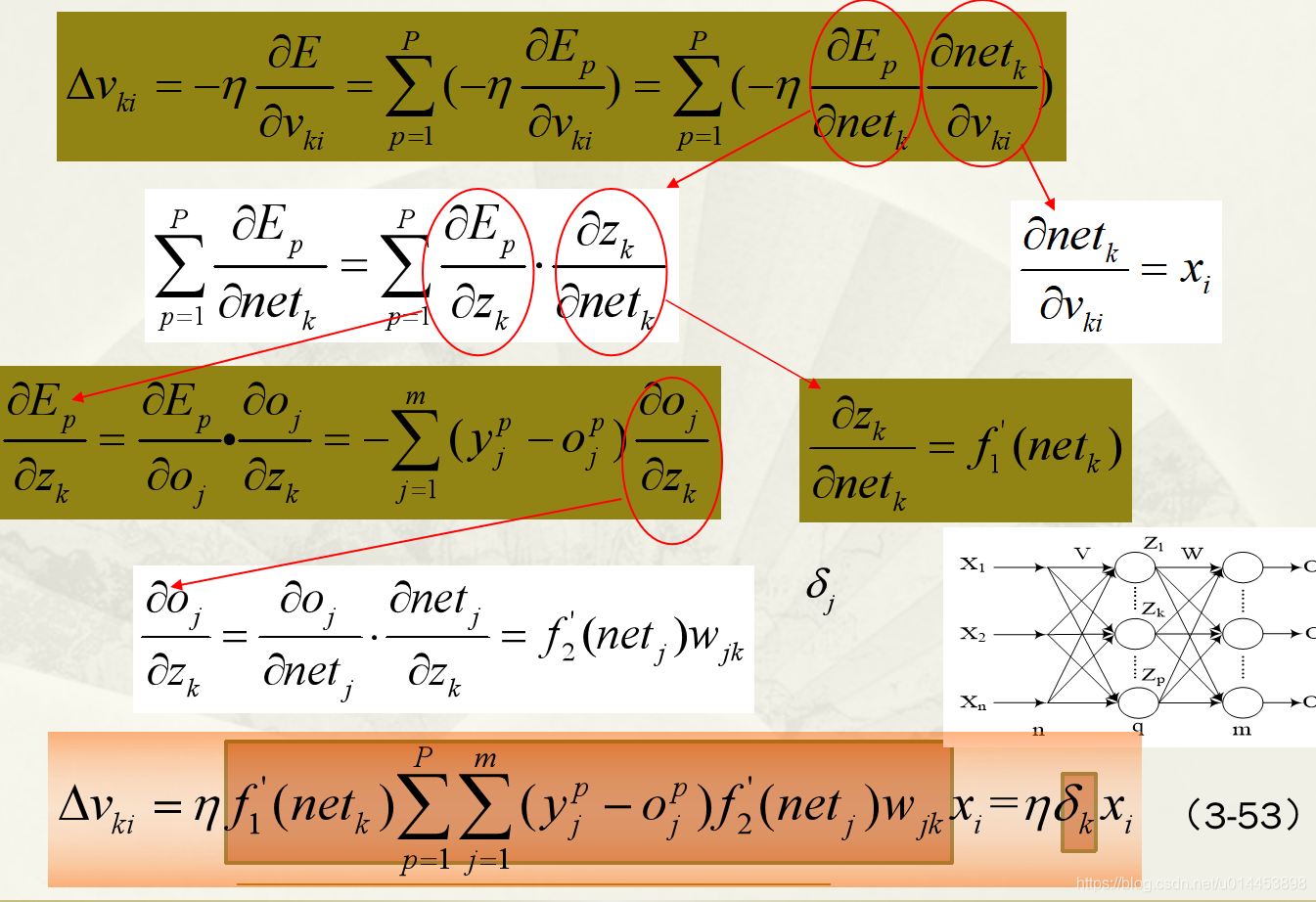
所以(3-53) 为输入层到隐藏层权值Vki的调整量公式。
从W和V的调整量公式可以看出,W 为隐藏层到输出层的权值,W的调整量公式带有一个激活函数f2的导数。
而V离输出层隔了两层,因此V的调整量公式不仅与输出层的激活函数f2有关,还与隐藏层的激活函数f1有关。
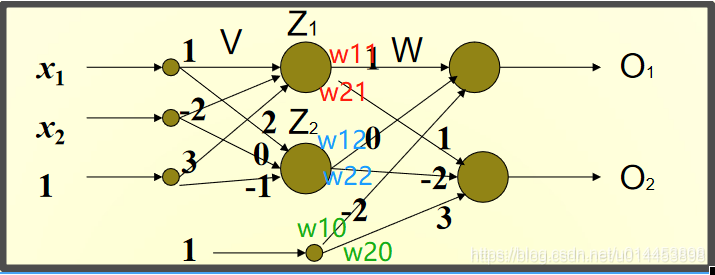
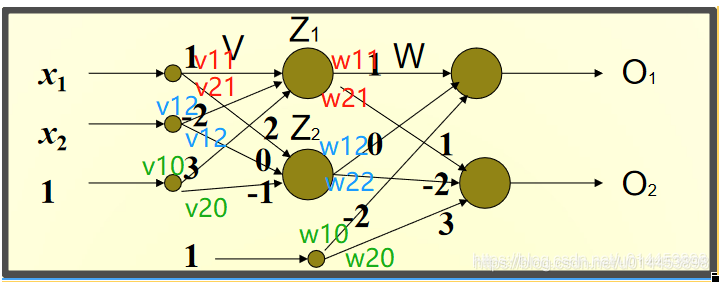
四:例子(一层隐藏层的BP网络)

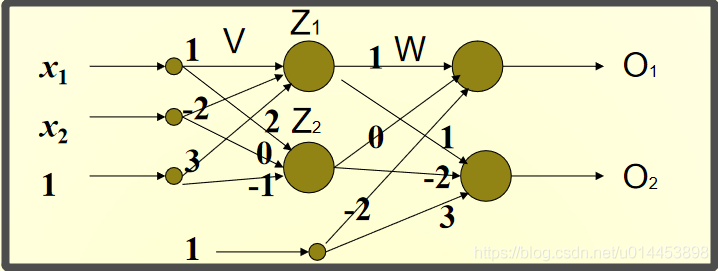
Z1神经元对应的权重向量为V1 = [1, -2, 3](初始值)
Z2神经元对应的权重向量V2 = [2, 0, -1](初始值)
O1神经元对应的权重向量W1 = [1, 0, -2](初始值)
O2神经元对应的权重向量W2 = [1, -2, 3](初始值)
首先计算神经元的输出
计算隐藏层神经元Z1和Z2的中间状态netZ1和netZ2:
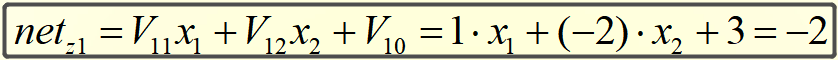
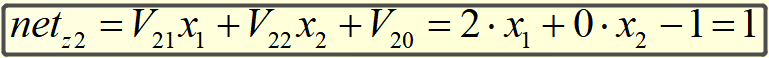
则Z1和Z2的输出为:
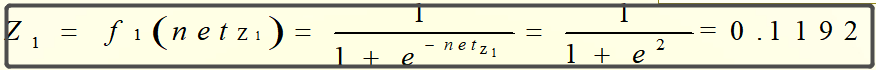
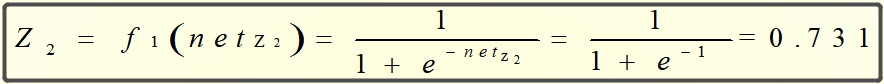
同理,可得神经元O1和O2的中间状态netO1和netO2:
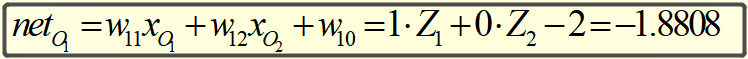
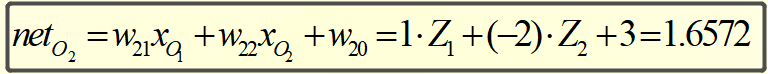
则O1和O2的输出为:
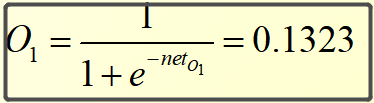
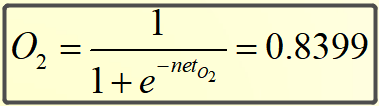
接下来开始通过误差反向调整权重
总结一下现在我们知道的条件:

由第二部分我们得出W权重的调整式子:

其中y为期望输出,o为网络输出,暂且把绿框部分称为”输出层的误差“
计算输出层的误差:

同理,O2的误差为:
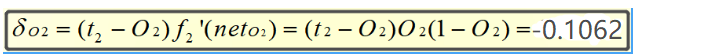
算出输出层误差后,就可以计算权重变化了:
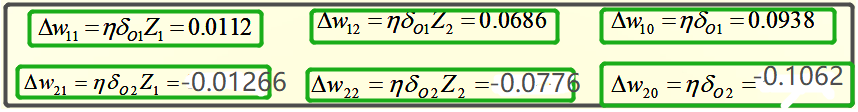
接下来计算隐藏层权重变化:
把上面黄色框内容称为”隐藏层的误差“
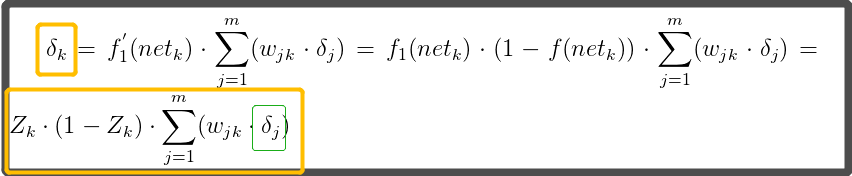
计算”隐藏层的误差“:
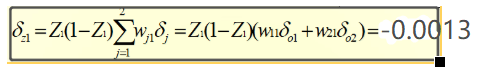
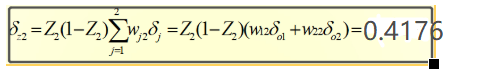
同样的,算出隐藏层的误差后,权值V的调整量就能计算出来了:
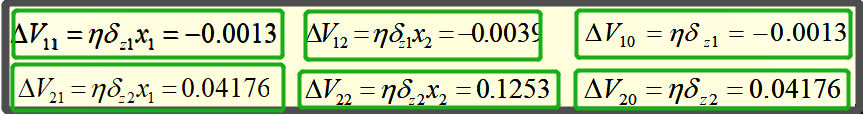
计算过程:
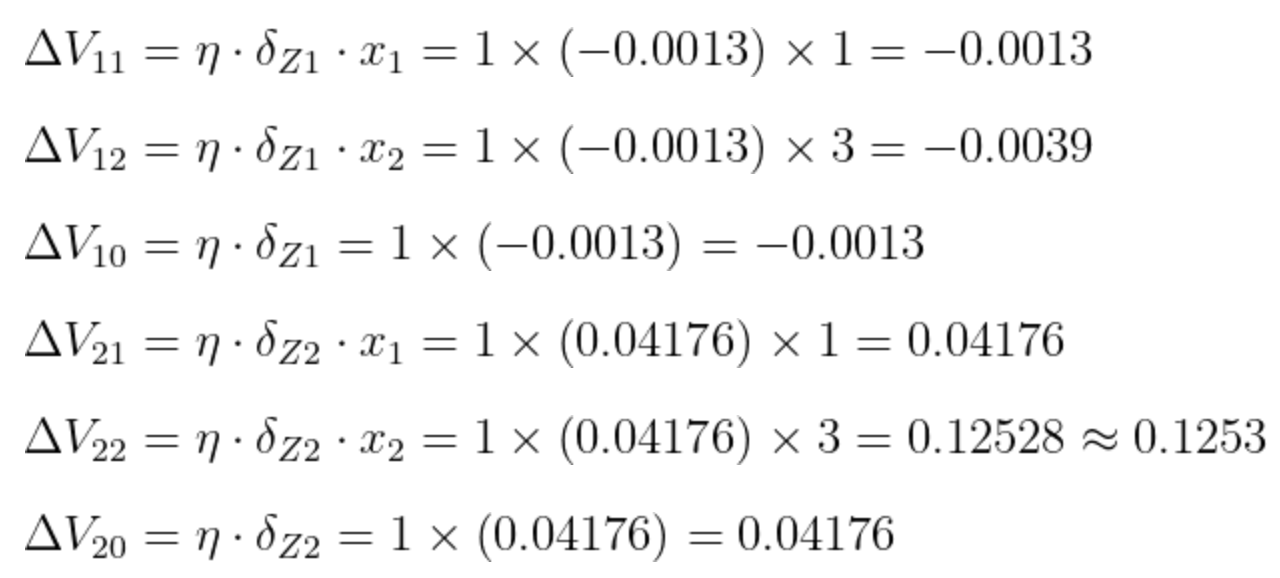
此时,所有W权值和所有V权值的调整量就算出来了。