神经网络--激活函数

神经网络–激活函数

参考文章：

https://blog.csdn.net/tyhj_sf/article/details/79932893

https://zhuanlan.zhihu.com/p/73214810

什么是激活函数

单一神经元模型如下图所示：

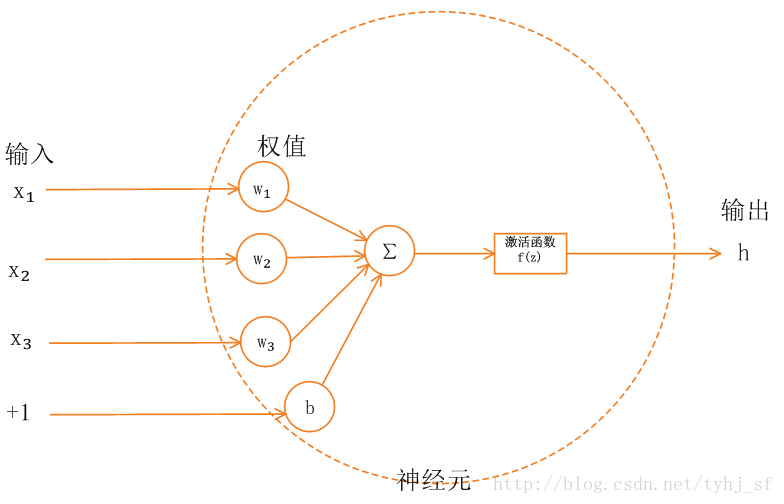
神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐层或输出层）。在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（又称激励函数）。

激活函数的用途

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

这里隐含一个信息就是激活函数一般都是非线性函数，如果我们借助空间的概念，更容易理解激活函数的意义，非线性的激活函数能带来的空间变化有以下几种：

升维、降维
放大、缩小
旋转
平移
弯曲

常见的激活函数

早期研究神经网络主要采用sigmoid函数或者tanh函数，输出有界，很容易充当下一层的输入。
近些年Relu函数及其改进型（如Leaky-ReLU、P-ReLU、R-ReLU等）在多层神经网络中应用比较多。

Sigmoid函数

Sigmoid 是常用的非线性的激活函数，它的数学形式如下：

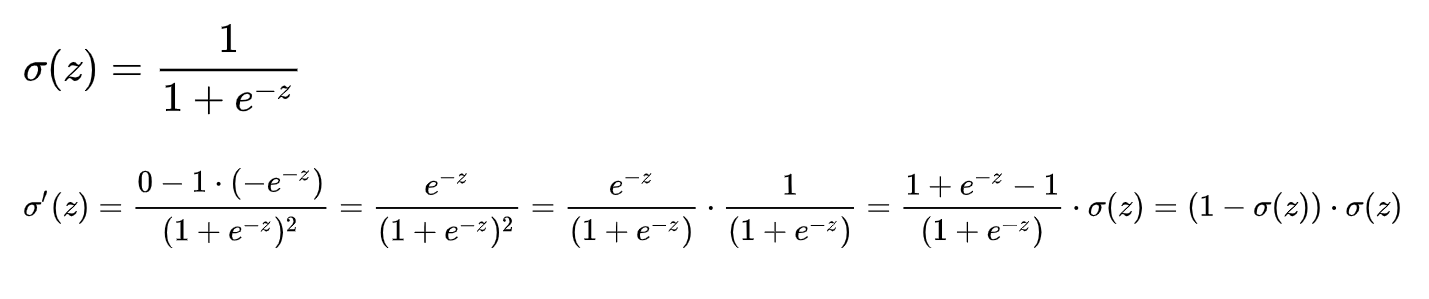
Sigmoid的几何图像如下：

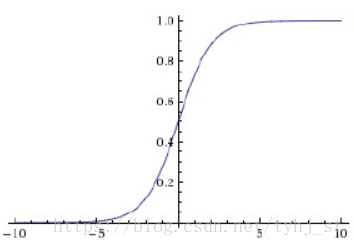
特点：它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1。

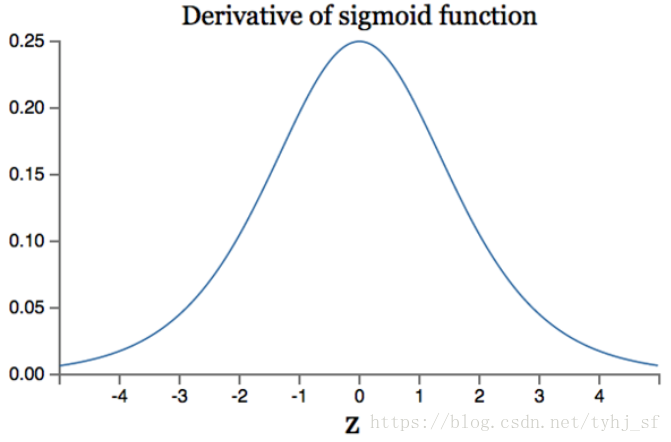
Sigmoid导数图像如下：

存在的缺点

激活函数计算量大（在正向传播和反向传播中都包含幂运算和除法）；
反向传播求误差梯度时，求导涉及除法；
Sigmoid导数取值范围是[0, 0.25]，由于神经网络反向传播时的“链式反应”，很容易就会出现梯度消失的情况。例如对于一个10层的网络，根据 $0.25^{10}\approx0.000000954$ ，第10层的误差相对第一层卷积的参数 $W_1$ 的梯度将是一个非常小的值，这就是所谓的“梯度消失”。
Sigmoid的输出不是0均值（即zero-centered）；这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布。

`Softmax`函数

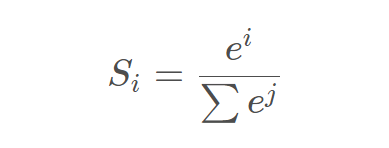
例如 V = [9,6,3,1] , 经过Softmax函数输出 V_Softmax = [0.950027342724 0.0472990762635 0.00235488234367 0.000318698668969]

以下是转化程序：

# -*- coding: utf-8 -*-
import math

V = [9,6,3,1]

v1 = math.exp(9)
v2 = math.exp(6)
v3 = math.exp(3)
v4 = math.exp(1)

v_sum = v1+v2+v3+v4

print(v1/v_sum,v2/v_sum,v3/v_sum,v4/v_sum)

可以看到，Softmax函数把输出映射成区间在(0,1)的值，并且做了归一化，所有元素的和累加起来等于1。

我们在做分类任务时，如果是二分类一般使用Sigmoid激活函数，如果是多分类一般使用Softmax函数。且这两中激活函数一般是在网络的最后一层使用，也就是输出层。

当在做二分类任务时，当输出在(0, 0.5)之间为一类，在(0.5, 1)之间为另一类；而在做多分类任务时，softmax的输出值可以直接当作概率，选取概率最大的分类作为预测的目标。

`tanh`函数

tanh为双曲正切函数，其英文读作Hyperbolic Tangent。tanh和 sigmoid 相似，都属于饱和激活函数，区别在于输出值范围由 (0,1) 变为了 (-1,1)，可以把 tanh 函数看做是 sigmoid 向下平移和拉伸后的结果。

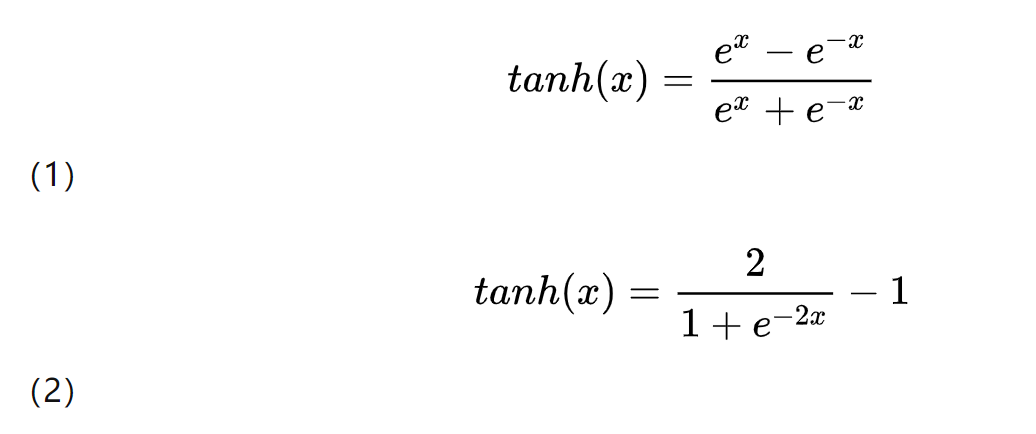
从公式2中，可以更加清晰看出tanh与sigmoid函数的关系（平移+拉伸）。

tanh函数及其导数的几何图像如下图：

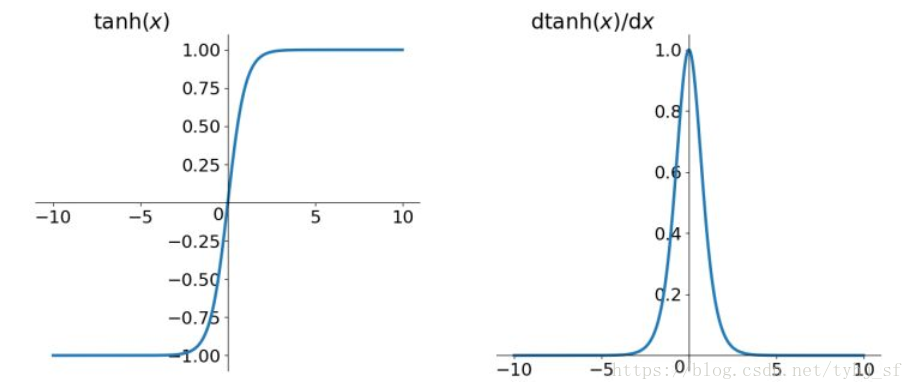
相比Sigmoid函数，

tanh的输出范围是(-1, 1)，解决了Sigmoid函数的不是zero-centered输出问题；
幂运算的问题仍然存在；
tanh导数范围在(0, 1)之间，相比sigmoid的(0, 0.25)，梯度消失（gradient vanishing）问题会得到缓解，但仍然还会存在。

`ReLU`函数

Relu函数的解析式：

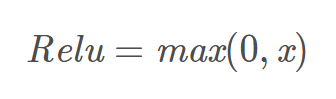
Relu函数及其导数的图像如下图所示：

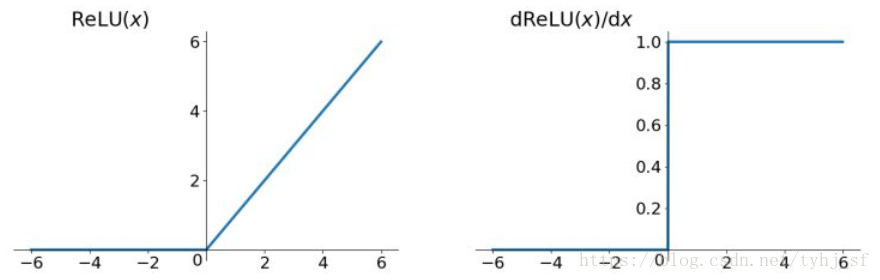
ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。

ReLU虽然简单，但却是近几年的重要成果，有以下几大优点：
1）解决了gradient vanishing问题 (在正区间)
2）计算速度非常快，只需要判断输入是否大于0
3）收敛速度远快于sigmoid和tanh

ReLU也有几个需要特别注意的问题：
1）ReLU的输出不是zero-centered
2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。

有两个主要原因可能导致这种情况产生:

(1) 非常不幸的参数初始化，这种情况比较少见

(2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。

解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！