KNN 分类算法

发表于 | 分类于

KNN分类算法

KNN是机器学习种最简单的分类算法，而图像分类也是图像识别种最简单的问题，所以这里使用KNN来做图像分类，帮忙大家初步了解图像识别算法。

KNN（K-NearestNeighbor）,即K-最近邻算法，顾名思义，找到最近的k个邻居，在前k个最近样本(k近邻)中选择最近的占比最高的类别作为预测类别。

KNN算法的计算逻辑：

  1. 给定测试对象，计算它与训练集中每个对象的距离；
  2. 圈定距离最近的k个训练对象，作为测试对象的邻居；
  3. 根据这k个近邻对象所属的类别，找到占比最高的那个类别作为测试对象的预测类别。

在KNN中，有两个方面的因素会影响KNN算法的准确度：一个是距离计算，另一个是k的选择。

一般使用两种比较常见的距离公式计算距离：

  1. 曼哈顿距离：
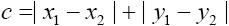
  2. 欧式距离：

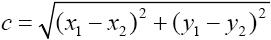
KNN算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import matplotlib.pyplot as plt


class KNNClassify:

    @staticmethod
    def create_data_set():
        _group = np.array([[1.0, 2.0], [1.2, 0.1], [0.1, 1.4], [0.3, 3.5], [1.1, 1.0], [0.5, 1.5]])
        _labels = np.array(['A', 'A', 'B', 'B', 'A', 'B'])
        return _group, _labels
    

if __name__ == "__main__":
    group, labels = KNNClassify.create_data_set()
    plt.scatter(group[labels == 'A', 0], group[labels == 'A', 1], color='r', marker='*')
    plt.scatter(group[labels == 'B', 0], group[labels == 'B', 1], color='g', marker='+')
    plt.show()

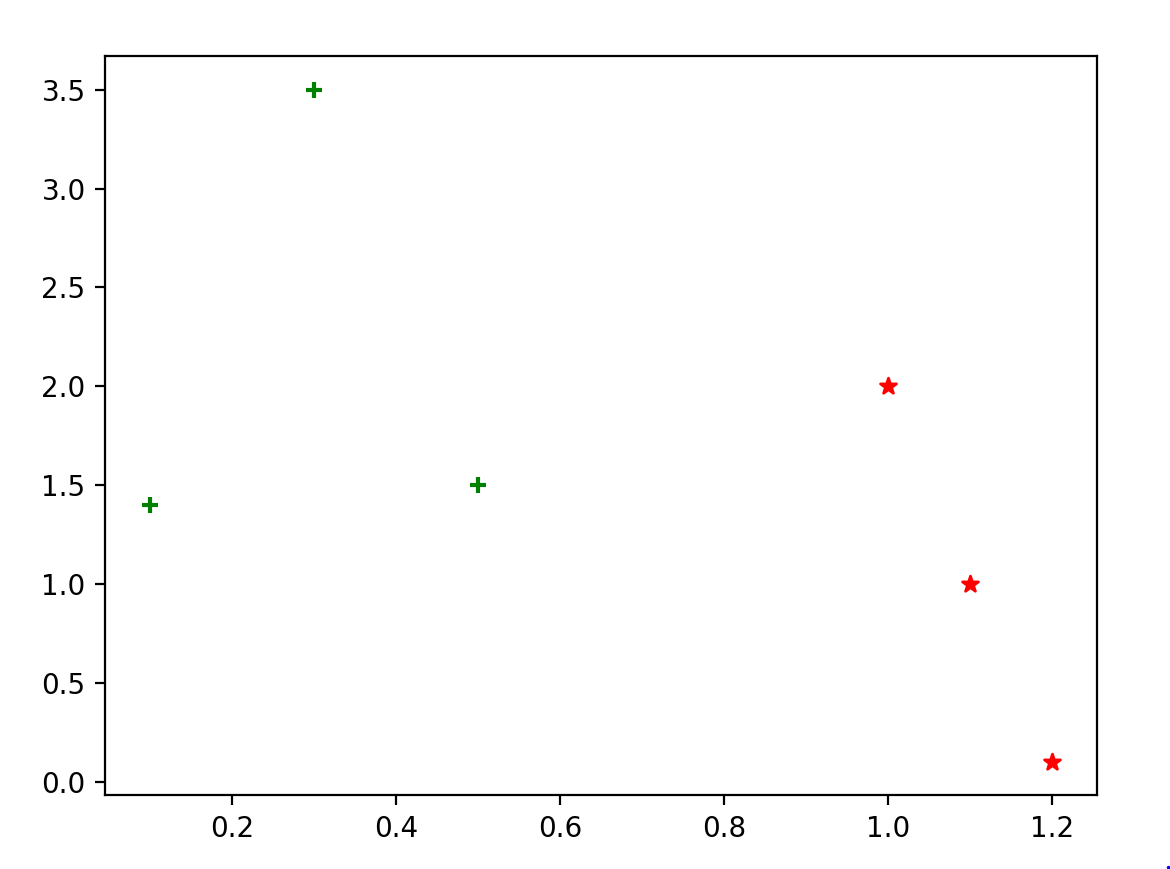
我们先创建一个简单的数据集，然后使用Matplotlib绘制图形，可以直观看到地查看数据分布情况。

接下来实现KNN算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import operator


class KNNClassify:
    
    # KNN 分类
    @staticmethod
    def knn_classify(k, dis, x_train, y_train, x_test):
        assert dis == 'E' or dis == 'M', 'dis must E or M, E代表欧式距离， M代表曼哈顿距离'
        num_test = x_test.shape[0]
        label_list = []

        for i in range(num_test):
            # 将测试数据复制为多份,方便直接利用矩阵进行快速计算
            x_test_temp = np.tile(x_test[i], (x_train.shape[0], 1))
            # 矩阵减法 相同位置分别相减
            if dis == 'E':   # 使用欧式距离公式作为距离度量
                result_temp = (x_train - x_test_temp) ** 2
                # axis=1 计算的是行的和，结果以列展示
                result_sum_temp = result_temp.sum(axis=1)
                # 最后再求平方根
                distances = np.sqrt(result_sum_temp)
            else:  # 使用曼哈顿公式作为距离度量
                result_temp = np.abs(x_train - x_test_temp)
                # axis=1 计算的是行的和，结果以列展示
                distances = result_temp.sum(axis=1)
            # 距离由小到大进行排序，并返回index值
            nearest_k = distances.argsort()
            top_k = nearest_k[:k]
            class_count = {}
            for index in top_k:
                class_count[y_train[index]] = class_count.get(y_train[index], 0) + 1
            sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
            label_list.append(sorted_class_count[0][0])
        return np.array(label_list)

最后测试下KNN算法的效果：

1
2
3
# 使用曼哈顿距离和欧式距离得到的预测结果不一样 E: ['A', 'B']  M: ['A', 'A']
y_test_pred = KNNClassify.knn_classify(1, 'E', group, labels, np.array([[1.0, 2.1], [0.4, 2.0]]))
print(y_test_pred)

注意，输入测试集的时候，需要将其转换为Numpy矩阵，否则系统会提示传入的参数是list类型，没有shape的方法。

KNN实现MNIST数据分类

下载和准备数据集

MNIST数据集是手写数字的图片数据集，MNIST可以直接通过pytorch进行下载与读取（也可以自行下载，然后放到相关目录，使用pytorch解析）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import torch
import numpy as np
from torch.utils.data import DataLoader
from torchvision import datasets


class MNIST:

    def __init__(self):
        self._batch_size = 100
        self._train_data_set = None
        self._test_data_set = None
        self._train_loader = None
        self._test_loader = None

    def init_data(self):
        # MNIST data_set
        self._train_data_set = datasets.MNIST(
            root='/ml_dataset/pymnist',  # 选择数据保存路径
            train=True,          # 选择训练集
            transform=None,      # 不考虑使用任何数据预处理
            download=True        # 从网络上下载图片
        )

        self._test_data_set = datasets.MNIST(
            root='/ml_dataset/pymnist',
            train=False,           # 选择测试集
            transform=None,
            download=True
        )

        # 加载数据
        self._train_loader = torch.utils.data.DataLoader(
            dataset=self._train_data_set,
            batch_size=self._batch_size,
            shuffle=True      # 将数据打乱
        )

        self._test_loader = torch.utils.data.DataLoader(
            dataset=self._test_data_set,
            batch_size=self._batch_size,
            shuffle=True
        )

        print("train_data:", self._train_data_set.data.size())
        print("train_labels:", self._train_data_set.targets.size())
        print("test_data:", self._test_data_set.data.size())
        print("test_labels:", self._test_data_set.targets.size())

if __name__ == "__main__":
    mnist = MNIST()
    mnist.init_data()

首次运行代码会自动下载数据到目录/ml_dataset/pymnist，如果运行时速度过慢，可以上网查询MNIST下载方式，将下载好的数据包，放置该目录，程序会自动解析。

train_dataset与test_dataset可以返回训练集数据、训练集标签、测试集数据以及测试集标签，训练集数据以及测试集数据都是n×m维的矩阵，这里的n是样本数（行数），m是特征数（列数）。训练数据集包含60 000个样本，测试数据集包含10 000个样本。

在MNIST数据集中，每张图片均由28×28个像素点构成，每个像素点使用一个灰度值表示。在这里，我们将28×28的像素展开为一个一维的行向量，这些行向量就是图片数组里的行（每行784个值，或者说每行就代表了一张图片）。训练集标签以及测试标签包含了相应的目标变量，也就是手写数字的类标签（整数0～9）。

上面代码打印的结果为：

1
2
3
4
train_data: torch.Size([60000, 28, 28])
train_labels: torch.Size([60000])
test_data: torch.Size([10000, 28, 28])
test_labels: torch.Size([10000])

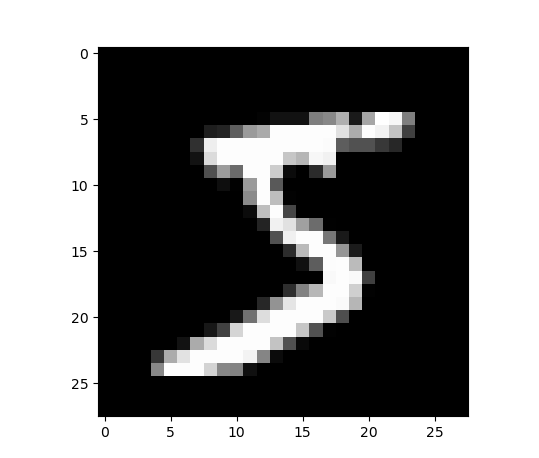
如果大家对这个数据集不是很了解，可以尝试多去显示几张图片看下，并查看相应的标签。

例如：

1
2
3
4
5
6
# 查看mnist数据集的图像是啥样的
def show_data_example(self):
    digit = self._train_loader.dataset.data[0]
    plt.imshow(digit, cmap='gray')
    plt.show()
    print(self._train_loader.dataset.targets[0])

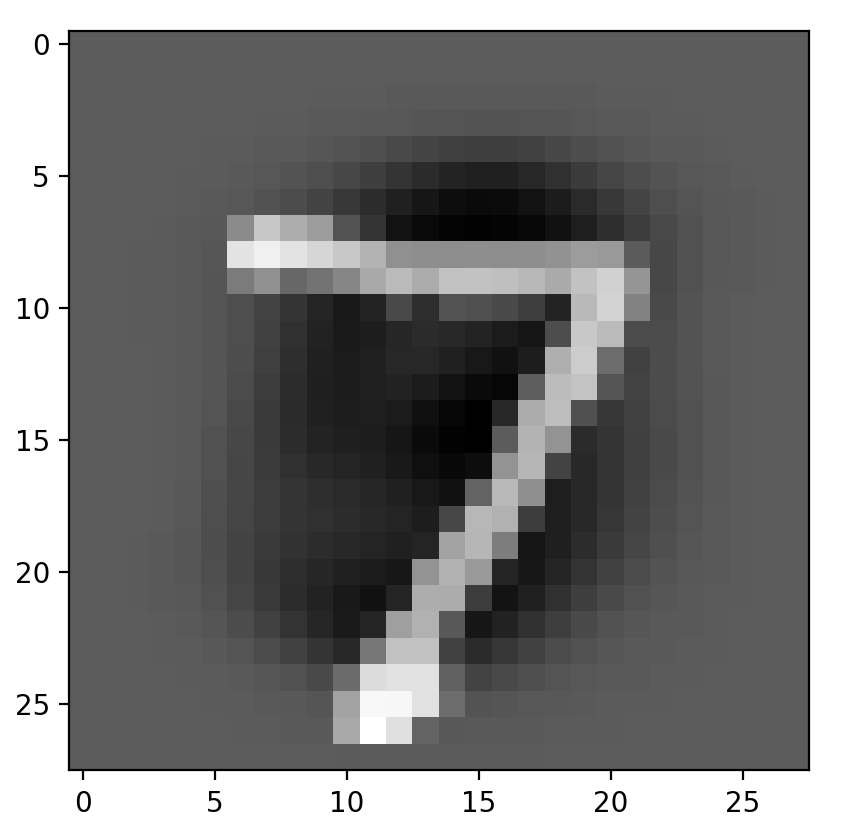
数字5：

原理剖析

在真正使用Python实现KNN算法之前，我们先来剖析一下思想，这里我们以MNIST的60 000张图片作为训练集，我们希望对测试数据集的10 000张图片全部打上标签。KNN算法将会比较测试图片与训练集中每一张图片，然后将它认为最相似的那个训练集图片的标签赋给这张测试图片。

那么，具体应该如何比较这两张图片呢？在本例中，比较图片就是比较28×28的像素块。最简单的方法就是逐个像素进行比较，最后将差异值全部加起来

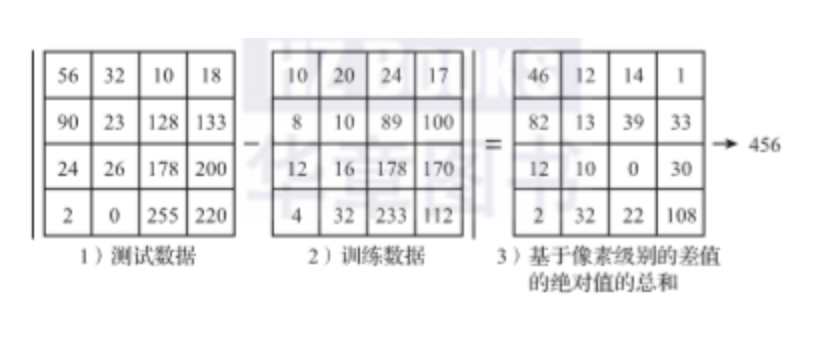
两张图片使用L1距离(曼哈顿距离，相应的L2距离是欧式距离)来进行比较。逐个像素求差值，然后将所有差值加起来得到一个数值。如果两张图片一模一样，那么L1距离为0，但是如果两张图片差别很大，那么，L1的值将会非常大。

验证KNN在MNIST上的效果

我们直接利用上面实现的KNN算法来测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from KNN import KNNClassify

class MNIST:
    
    def predict(self):
        # 需要转为numpy矩阵
        x_train = self._train_loader.dataset.data.numpy()
        # 需要reshape之后才能放入knn分类器
        x_train = x_train.reshape(x_train.shape[0], 28*28)
        y_train = self._train_loader.dataset.targets.numpy()
        x_test = self._test_loader.dataset.data[:1000].numpy()
        x_test = x_test.reshape(x_test.shape[0], 28*28)
        y_test = self._test_loader.dataset.targets[:1000].numpy()

        num_test = y_test.shape[0]
        y_test_pred = KNNClassify.knn_classify(5, 'M', x_train, y_train, x_test)
        correct_arrays = np.array(y_test == y_test_pred)
        num_correct = correct_arrays.sum()
        accuracy = float(num_correct) / num_test
        print(f'Got {num_correct}/{num_test} => accuracy: {accuracy}')

这里需要多说点，上面的KNN算法实现，我是当作一个单独的脚本，这里的MNIST数据分类，是另一个脚本，且位于同一文件夹下：

直接在MNIST.py脚本中使用from KNN import KNNClassify可能会出错，需要在__init__.py中添加一行代码：from .KNN import KNNClassify。

最后运行代码，Got 368 / 1000 correct => accuracy: 0.368000！这说明1000张图片中有368张图片预测类别的结果是准确的。

先别气馁，我们之前不是刚说过可以使用数据预处理的技术吗？下面我们试一下如果在进行数据加载的时候尝试使用归一化，那么分类准确度是否会提高呢？

我们稍微修改下代码,主要是在将X_train和X_test放入KNN分类器之前先调用centralized，进行归一化处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class MNIST:
    
    @staticmethod
    def get_x_mean(x_train):
        # 我只关心我需要转换成x_train.shape[0]行，列数自己计算（转换成60000*784）
        x_train = x_train.reshape(x_train.shape[0], -1)  # Turn the image to 1-D
        # 每行是一张图片 求每一列均值。即求所有图片每一个像素上的平均值
        mean_image = x_train.mean(axis=0)
        return mean_image

    @staticmethod
    def centralized(x_test, mean_image):
        x_test = x_test.reshape(x_test.shape[0], -1)
        x_test = x_test.astype(np.float64)
        x_test -= mean_image  # Subtract the mean from the graph, and you get zero mean graph
        return x_test

    # 归一化后预测
    def predict_centralized(self):
        x_train = self._train_loader.dataset.data.numpy()
        mean_image = self.get_x_mean(x_train)
        x_train = self.centralized(x_train, mean_image=mean_image)
        y_train = self._train_loader.dataset.targets.numpy()
        x_test = self._test_loader.dataset.data[:1000].numpy()
        x_test = self.centralized(x_test, mean_image)
        y_test = self._test_loader.dataset.targets[:1000].numpy()
        num_test = y_test.shape[0]
        y_test_pred = KNNClassify.knn_classify(5, 'M', x_train, y_train, x_test)
        correct_arrays = np.array(y_test == y_test_pred)
        num_correct = correct_arrays.sum()
        accuracy = float(num_correct) / num_test
        print(f'Got {num_correct}/{num_test} => accuracy: {accuracy}')

下面再来看下输出结果的准确率：Got 951 / 1000 correct => accuracy: 0.951000，95%算是不错的结果。

现在我们来看一看归一化后的图像是什么样子的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class MNIST:
    
    def show_data_centralized(self):
        x_train = self._train_loader.dataset.data.numpy()
        mean_image = self.get_x_mean(x_train)
        x_test = self._test_loader.dataset.data[:1000].numpy()
        c_data = self.centralized(x_test, mean_image)
        c_data = c_data.reshape(c_data.shape[0], 28, 28)
        plt.imshow(c_data[0], cmap='gray')
        plt.show()
        print(self._test_loader.dataset.targets[0])  # 输出的标签为7
        

if __name__ == "__main__":
    mnist = MNIST()
    mnist.init_data()
    mnist.show_data_example()
    # 无任何数据预处理，M: 36.8% E: 27%
    # mnist.predict()

    # 归一化后，准确率大大提升 M:95.1% E: 96.3%
    # mnist.predict_centralized()
    # 查看归一化后的图像与原图像有啥区别
    mnist.show_data_centralized()

所以是否了解到数据预处理的重要性了？！未进行数据预处理的准确率只有36.8%,进行归一化数据预处理后，准确率提升至95%！

在开始使用算法进行图像识别之前，良好的数据预处理能够很快达到事半功倍的效果。图像预处理不仅可以使得原始图像符合某种既定规则以便于进行后续的处理，而且可以帮助去除图像中的噪声。

在后续讲解神经网络的时候我们还会了解到，数据预处理还可以帮助减少后续的运算量以及加速收敛。常用的图像预处理操作包括归一化、灰度变换、滤波变换以及各种形态学变换等。

归一化可用于保证所有维度上的数据都在一个变化幅度上。比如，在预测房价的例子中，假设房价由面积s和卧室数b决定，面积s在0～200之间，卧室数b在0～5之间，进行归一化的一个实例就是s=s/200，b=b/5。

KNN实现Cifar10数据分类

Cifar10是一个由彩色图像组成的分类的数据集（MNIST是黑白数据集），其中包含了飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船、卡车10个类别，且每个类中包含了1000张图片。整个数据集中包含了60 000张32×32的彩***片。该数据集被分成50 000和10 000两部分，50 000是training set，用来做训练；10 000是test set，用来做验证。

下载和准备数据集

同样的你可以通过Pytorch直接下载该数据集，或者自己从数据集官网下载，然后放置指定目录，程序会自动解析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import torch
import numpy as np
from torch.utils.data import DataLoader
import torchvision.datasets as datasets
import matplotlib.pyplot as plt

from KNN import KNNClassify


class Cifar10:

    def __init__(self):

        self._batch_size = 100
        self._train_data_set = None
        self._test_data_set = None
        self._train_loader = None
        self._test_loader = None

    def init_data(self):
        self._train_data_set = datasets.CIFAR10(
            root='/ml_dataset/pycifar',
            train=True,
            download=True
        )
        self._test_data_set = datasets.CIFAR10(
            root='/ml_dataset/pycifar',
            train=False,
            download=True
        )

        self._train_loader = torch.utils.data.DataLoader(
            dataset=self._train_data_set,
            batch_size=self._batch_size,
            shuffle=True
        )
        self._test_loader = torch.utils.data.DataLoader(
            dataset=self._test_data_set,
            batch_size=self._batch_size,
            shuffle=True
        )

如果对数据集不了解，可以查看数据集的图片内容

1
2
3
4
5
6
7
8
class Cifar10
    
    def show_data_example(self):
        classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
        digit = self._train_loader.dataset.data[0]
        plt.imshow(digit)
        plt.show()
        print(classes[self._train_loader.dataset.targets[0]])  # 打印出是frog

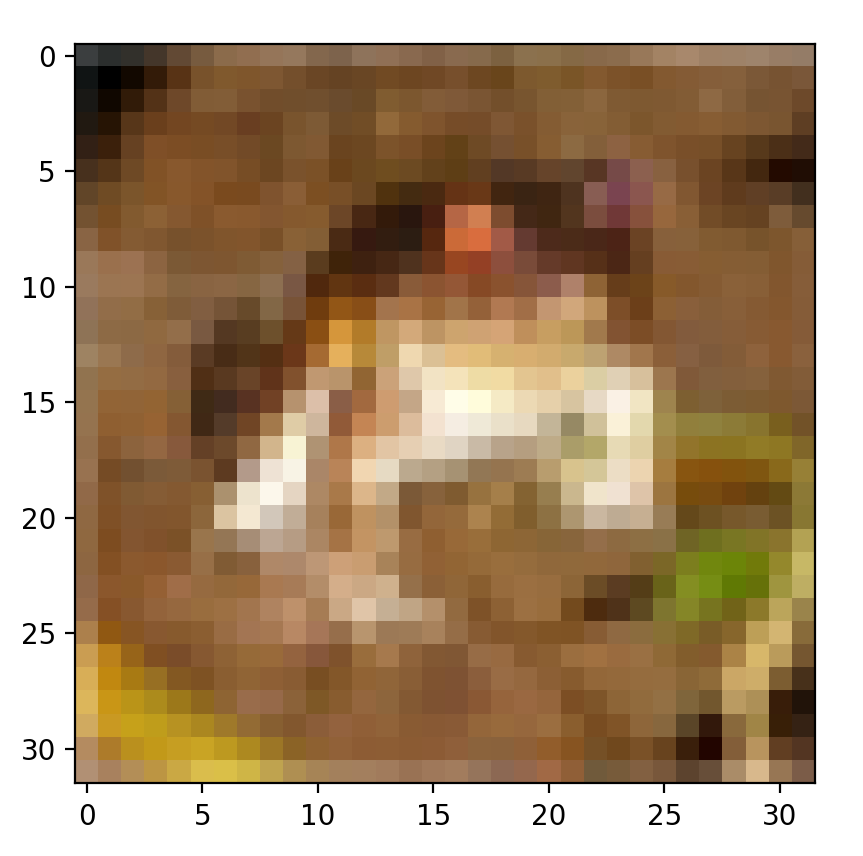
classes是我们定义的类别，其对应的是Cifar中的10个类别。使用PyTorch读取的类别是index，所以我们还需要额外定义一个classes来指向具体的类别。由于只有32×32个像素，因此图像比较模糊。

验证KNN在Cifar10上的效果

现在我们主要观察下KNN对于Cifar10数据集的分类效果，与之前MNIST数据集不同的是，X_train = train_loader.dataset.train_data，X_train的dtype是uint8而不是torch.uint8，所以不需要使用numpy()这个方法进行转换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Cifar10:
    
    def predict(self):
        # 这个数据集无需使用numpy()转换
        x_train = self._train_loader.dataset.data
        mean_image = self.get_x_mean(x_train)
        x_train = self.centralized(x_train, mean_image=mean_image)
        y_train = self._train_loader.dataset.targets
        x_test = self._test_loader.dataset.data[:100]
        x_test = self.centralized(x_test, mean_image)
        y_test = self._test_loader.dataset.targets[:100]
        num_test = len(y_test)
        # 这里设置了k=6，可以更换其他值试一下准确率是否有改变
        # k=6 acc:0.33  k=8 acc:0.3
        y_test_pred = KNNClassify.knn_classify(8, 'E', x_train, y_train, x_test)
        correct_arrays = np.array(y_test == y_test_pred)
        num_correct = correct_arrays.sum()
        accuracy = float(num_correct) / num_test
        print(f'Got {num_correct}/{num_test} => accuracy: {accuracy}')

经过验证，KNN算法在Cifar10数据集上的准确率不高，大概只有30%的准确率，而且是在归一化处理的基础上。

总结

前面我们讲了影响KNN算法的两大因素分别为距离度量算法和K的取值，也就是算法的两个超参数，到底如何选取这两个值，就是一个模型调参的问题，这个过程一般就是需要你自己去测试，选取一个效果比较好的取值。

虽然KNN在MNIST数据集中的表现还算可以(主要原因可能是MNIST是灰度图)，但是其在Cifar10数据集上的分类准确度就差强人意了。另外，虽然KNN算法的训练不需要花费时间（训练过程只是将训练集数据存储起来），但由于每个测试图像需要与所存储的全部训练图像进行比较，因此测试需要花费大量时间，这显然是一个很大的缺点，因为在实际应用中，我们对测试效率的关注要远远高于训练效率。

在实际的图像分类中基本上是不会使用KNN算法的。因为图像都是高维度数据（它们通常包含很多像素），这些高维数据想要表达的主要是语义信息，而不是某个具体像素间的距离差值（在图像中，具体某个像素的值和差值基本上并不会包含有用的信息），所以这就是我们为什么需要用深度学习和神经网络来训练模型提高准确率和检测速度。