PyTorch实现卷积神经网络

发表于 | 分类于

PyTorch实现卷积神经网络

关于卷积神经网络的一些基础知识和概念等前面已经多次学习，这篇文章的重点是Pytorch来实现卷积神经网络，偏向于代码实践，理论知识不多，不过有一点关于图像经过卷积后的输出尺寸问题的公式我觉得不错，值得记录。

卷积层

我们知道卷积的过程是：让卷积核在图片上依次进行滑动，滑动方向为从左到右，从上到下，每滑动一次，卷积核就与其滑窗位置对应的输入图片x做一次点击运算并得到一个数值。在卷积的过程中，一般情况下，图片的宽高会变得越来越小，而通道数会变得越来越多。这里尺寸改变有什么样的规律呢？

输入1*7的向量，经过1*3的卷积，如果步长为2，最终得到一个1*5的向量；如果步长为2，最终得到一个1*3的向量

输入7*7的向量，经过3*3的卷积，如果步长为1，最终得到一个5*5的向量；如果步长为2，最终得到一个3*3的向量；如果步长为3，会报错

上面的例子卷积核个数都是1且通道数也是1，下面考虑多个卷积核的情况

输入32*32*3的图片，如果kernel大小为5*5*3(实际上大小就是5*5，后面的3只是为了表示针对3通道图片的一种写法，卷积核会对三个通道分别实行5*5卷积，然后加到一起)，单个卷积核和步长为1的情况下，最终得到一个28*28*1的新图片；如果我们连续堆叠6个不同的卷积，最终特征层将得到6个通道，即28*28*6的新图片。

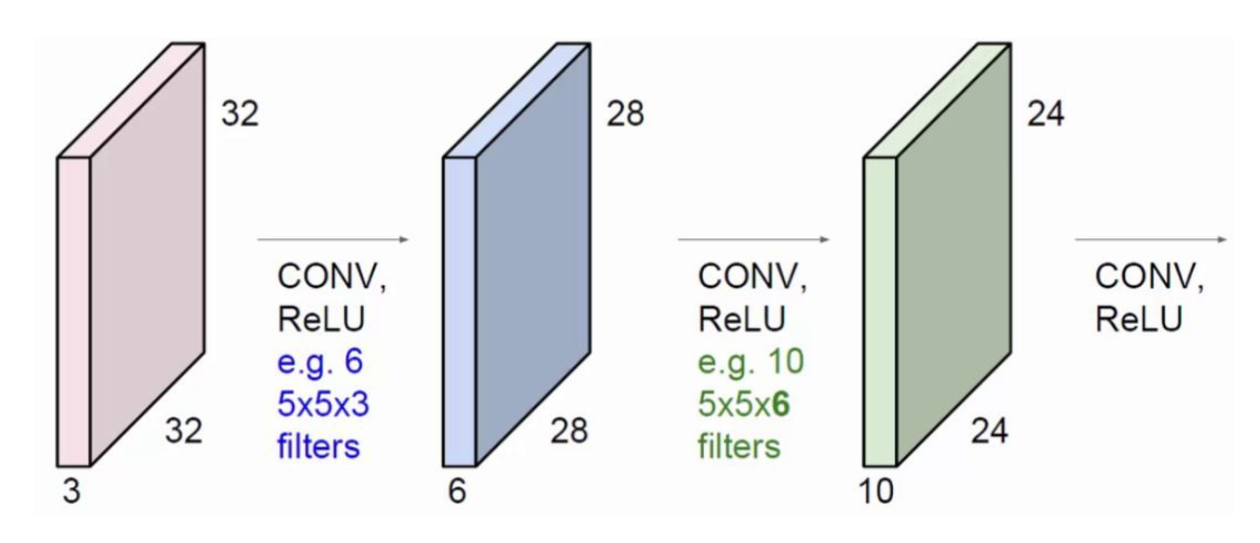
，在7*7的输入图片周边做一个像素的填充(pad=1,周边填充是上下左右都会填充),如果步长为1，kernel为3*3的卷积输出的特征层为7*7。

所以可以总结出一种通用的卷积层计算公式：输入图片为W1*H1*D1(字母分别表示图像的宽、高、channel)，卷积层的参数中kernel大小为F*F，步长为S，pad大小为P，kernel个数为K，那么经过卷积后，输出图像的宽、高、channel分别为：

1
2
3
4
5
W2 = (W1-F+2P)/S + 1

H2 = (H1-F+2P)/S + 1

D2 = K

其实关于这个计算公式倒是不用刻意的去记忆，理解了卷积的原理，那么关于卷积后的图片尺寸大小，很容易就能得出，完全用不到公式。

PyTorch中的卷积函数代码：

1
2
3
import torch.nn as nn

nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding, dilation, groups, bias)

参数说明

  • in_channels(int)：输入图片的channel
  • out_channels(int)：输出图片（特征层）的channel
  • kernel_size(int or tuple)：kernel的大小
  • stride(int or tuple, optional)：卷积的步长，默认为1
  • padding(int or tuple, optional)：四周pad的大小，默认为0
  • dilation(int or tuple, optional)：kernel元素间的距离，默认为1
  • groups(int, optional)：将原始输入channel划分成的组数，默认为1
  • bias(bool, optional)：如果是True，则输出的Bias可学，默认为True

因为输出图片的通道数等于卷积核的个数，所以这里的out_channels参数可以理解为卷积核个数。

池化层

池化是对图片进行压缩(降采样)的一种方法，池化的方法有很多，如max pooling、average pooling等。池化层也有操作参数，我们假设输入图像为W1*H1*D1(字母分别表示图像的宽、高、channel)，池化层的参数中，池化kernel的大小为F*F，步长为S，那么经过池化后输出的图像宽、高、channel分别为：

1
2
3
W2 = (W1 - F)/S + 1
H2 = (H2 - F)/S + 1
D2 = D1

通常情况下，F=2,S=2。

一个4*4的特征层经过池化filter=2*2,stride=2的最大池化操作后可以得到一个2*2的特征层。

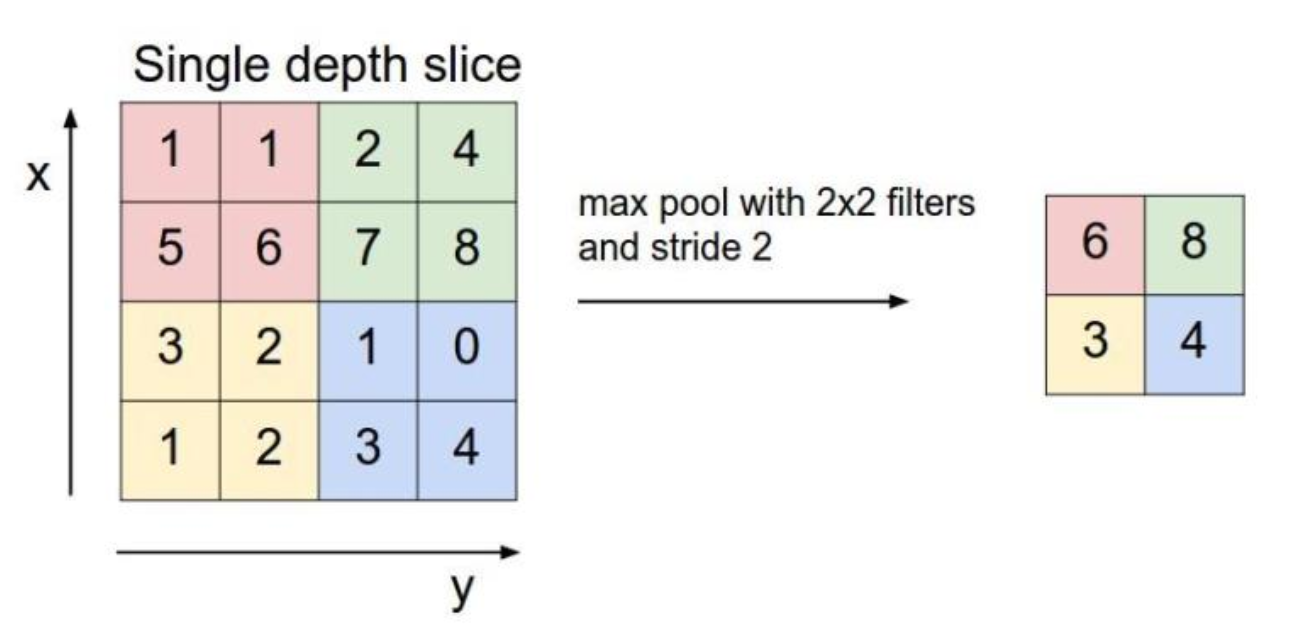
池化层对原始特征层的信息进行压缩，卷积层、池化层、激活层很多时候三者几乎像一个整体一样同时出现。

Pytorch定义卷积神经网络的代码（初版）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import torch.nn as nn
import torch.nn.functional as f


class CNN(nn.Module):

    # 定义卷积神经网络需要的元素
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, (5,))  # 定义第一个卷积层
        self.pool = nn.MaxPool2d(2, 2)  # 池化层
        self.conv2 = nn.Conv2d(6, 16, (5,))
        self.fc1 = nn.Linear(16*5*5, 120)  # 全连接层
        self.fc2 = nn.Linear(120, 84)      # 全连接层
        self.fc3 = nn.Linear(84, 10)       # 最后一个全连接层用作10分类

    def forward(self, x):
        # 第一个卷积层首先经过ReLU做激活，然后池化
        x = self.pool(f.relu(self.conv1(x)))
        # 第二个卷积层也先经过ReLU激活，然后池化
        x = self.pool(f.relu(self.conv2(x)))
        # 对特征层Tensor维度进行变换，使之符合预定义好的全连接层输入尺寸
        x = x.view(-1, 16*5*5)
        # 特征层经过第一次全连接层操作，然后通过ReLU激活
        x = f.relu(self.fc1(x))
        # 特征层经过第二次全连接层操作，然后通过ReLU激活
        x = f.relu(self.fc2(x))
        # 特征层经过最后一次全连接层操作，得到最终要分类的结果（10分类标签）
        x = self.fc3(x)
        return x


if __name__ == "__main__":
    net = CNN()
    print(net)

批规范化层(BatchNorm层，BN层)

批规范化层主要是为了加速神经网络的收敛过程以及提高训练过程中的稳定性。

batch的概念就是在使用卷积神经网络处理图像数据时，往往是几张图片(如32张、64张、128张等)被同时输入到神经网络中一起进行前向计算，误差也是将该batch中所有图片的误差累计起来一起回传。

BatchNorm方法其实就是对一个batch和中的数据根据公式做了归一化。

VGGNet

下面我们借助比较比较常见的VGG网络架构来进行了解Pytorch是如何实现卷积神经网络的。

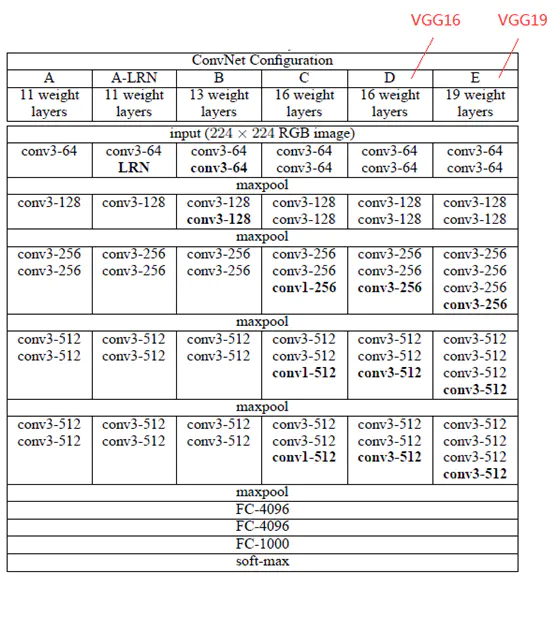
VGGNet包含两种结构，分别为16层和19层，VGG16包含了16个隐藏层（13个卷积层+3个全连接层），如图中的D列所示；VGG19包含了19个隐藏层（16个卷积层+3个全连接层），如图中的E列所示。

VGGNet结构中，所有的卷积层的kernel都只有3*3；其连续使用3组3*3 kernel（stride=1）的原因是它与使用1个7*7 kernel产生的效果相同，然而更深的网络结构还会学习到更复杂的非线性关系，从而使得模型的效果更好。

该操作带来的另一个好处是参数数量的减少，因为对于一个包含了C个kernel的卷积层来说，原来的参数个数为7*7*C，而新的参数个数为3*(3*3*C)。

VGG16的立体的网络结构图：（此部分内容参考文章：https://blog.csdn.net/weixin_38132153/article/details/107616764）

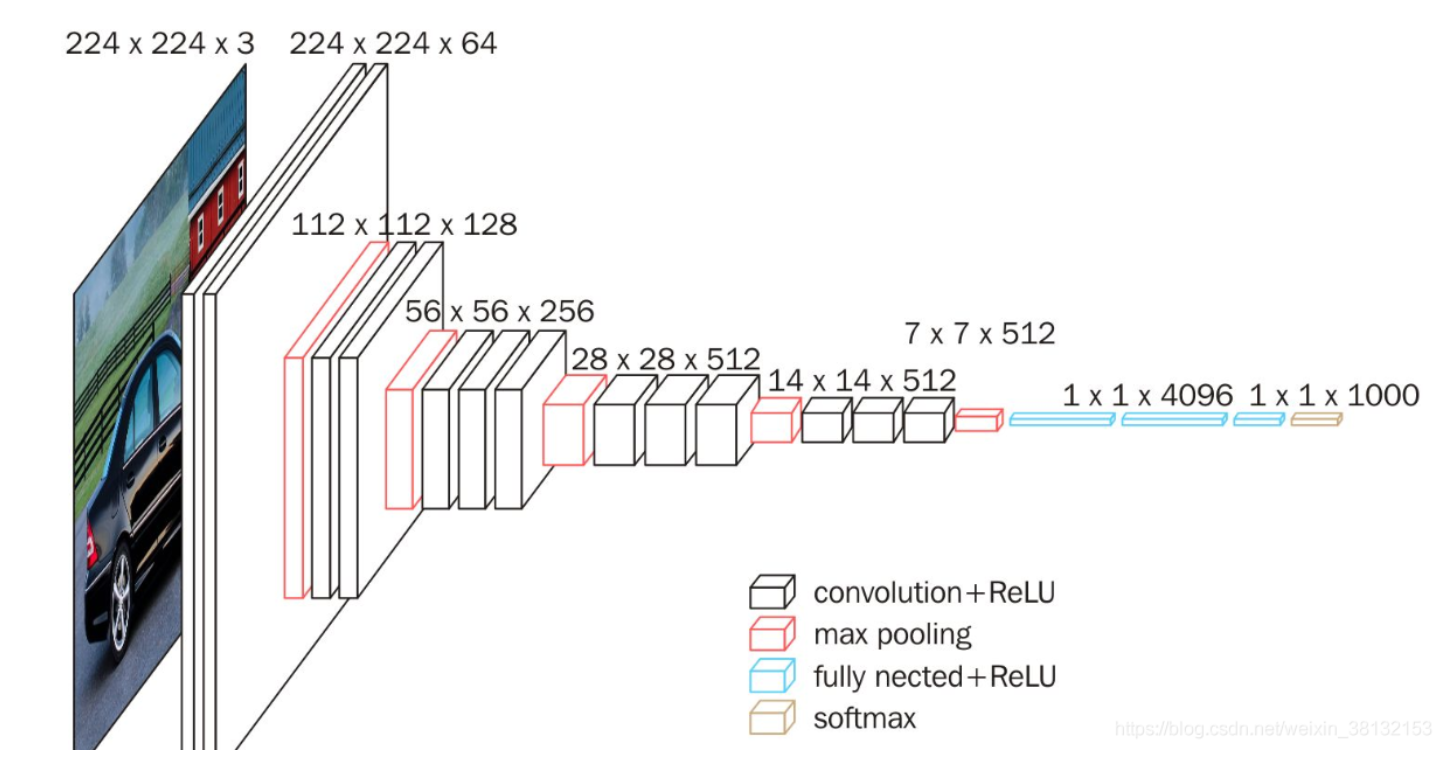
根据VGG16的网络结构，我们使用Pyotrch来个初步实现一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
import torch
from torch import nn
from torch import optim


class VGG16(nn.Module):

    # 指定输出类别数量
    def __init__(self, nums):
        super(VGG16, self).__init__()
        self.nums = nums
        vgg = list()

        # 第一个卷积部分 3*3 conv, 64
        # 初始输入通道数=3
        vgg.append(nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        # 下一层的输入通道数等于上一层的输出通道数
        vgg.append(nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        # 两个卷积层后接一个池化层
        vgg.append(nn.MaxPool2d(kernel_size=2, stride=2))

        # 第二个卷积部分 3*3 conv, 128
        vgg.append(nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=128, out_channels=128, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.MaxPool2d(kernel_size=2, stride=2))

        # 第三个卷积部分 3*3 conv, 256  从第三个部分开始，有三个卷积层
        vgg.append(nn.Conv2d(in_channels=128, out_channels=256, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.MaxPool2d(kernel_size=2, stride=2))

        # 第四个卷积部分 3*3 conv, 512
        vgg.append(nn.Conv2d(in_channels=256, out_channels=512, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.MaxPool2d(kernel_size=2, stride=2))

        # 第五个卷积部分 3*3 conv, 512
        vgg.append(nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, stride=1, padding=1))
        vgg.append(nn.ReLU())
        vgg.append(nn.MaxPool2d(kernel_size=2, stride=2))

        # 将每一个模块按照他们的顺序送入到nn.Sequential中,输入要么是predict,要么是一系列的模型，遇到上述的list，必须用*号进行转化
        self.main = nn.Sequential(*vgg)

        # 全连接层(in_features为什么是512*512*7很关键)
        # 另外，当输入图片尺寸非3*224*224时，in_features是不同的
        classification = list()
        # in_features四维张量变成二维[batch_size,channels,width,height]变成    [batch_size,channels*width*height]
        # 输出4096个神经元，参数变成512*7*7*4096+bias(4096)个
        classification.append(nn.Linear(in_features=512 * 7 * 7, out_features=4096))
        classification.append(nn.ReLU())
        classification.append(nn.Dropout(p=0.5))
        classification.append(nn.Linear(in_features=4096, out_features=4096))
        classification.append(nn.ReLU())
        classification.append(nn.Dropout(p=0.5))
        classification.append(nn.Linear(in_features=4096, out_features=self.nums))

        self.classification = nn.Sequential(*classification)

    def forward(self, x):
        feature = self.main(x)  # 输入张量x
        # reshape x变成[batch_size,channels*width*height]
        feature = feature.view(x.size(0), -1)  
        result = self.classification(feature)
        return result


x = torch.rand(size=(8, 3, 224, 224))
vgg16 = VGG16(nums=10)
out = vgg16(x)
print(out)
print(vgg16)

这里特别需要注意的一点就是，全连接层的输入值（in_features）,上面给出的网络结构图的尺寸值前提是在输入图片大小为3*224*224，所以经过全部卷积层后得到512*7*7的特征图，如果输入尺寸有变，那么全连接层的输入值是要自己改变的。

上面编写的初步版本我们很容易读懂是如何一步步实现的，但是经过观察思考我们可以发现，卷积部分代码存在许多重复的地方，如果我们可以编写一个方法，通过传入参数，自动实现卷积部分就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
 可以通过初始化参数指定生成VGG16 or VGG19网络模型
class VGG(nn.Module):

    cfg = {
        'VGG16': [
            64, 64, 'M',
            128, 128, 'M',
            256, 256, 256, 'M',
            512, 512, 512, 'M',
            512, 512, 512, 'M'
        ],
        'VGG19': [
            64, 64, 'M',
            128, 128, 'M',
            256, 256, 256, 256, 'M',
            512, 512, 512, 512, 'M',
            512, 512, 512, 512, 'M'
        ]
    }

    def __init__(self, net_name, out_put_nums):
        super(VGG, self).__init__()

        self.main = self._make_layers(net_name)

        # 全连接层(in_features为什么是512*512*7很关键)
        # 另外，当输入图片尺寸非3*224*224时，in_features是不同的
        classification = list()
        # in_features四维张量变成二维[batch_size,channels,width,height]变成[batch_size,channels*width*height]
        # 输出4096个神经元，参数变成512*7*7*4096+bias(4096)个
        classification.append(nn.Linear(in_features=512 * 7 * 7, out_features=4096))
        classification.append(nn.ReLU())
        classification.append(nn.Dropout(p=0.5))
        classification.append(nn.Linear(in_features=4096, out_features=4096))
        classification.append(nn.ReLU())
        classification.append(nn.Dropout(p=0.5))
        classification.append(nn.Linear(in_features=4096, out_features=out_put_nums))

        self.classification = nn.Sequential(*classification)

    def _make_layers(self, net_name):
        layers = []
        in_channels = 3  # 初始输入通道数量为3
        last_out_put = in_channels  # 上一层的输出通道数，初始时就是输入通道数
        for v in self.cfg[net_name]:

            if v == 'M':
                layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
            else:
                layers += [nn.Conv2d(last_out_put, v, kernel_size=3, padding=1),
                           nn.BatchNorm2d(v),
                           nn.ReLU(inplace=True)]
                last_out_put = v
        return nn.Sequential(*layers)

    def forward(self, _x):
        feature = self.main(_x)
        feature = feature.view(_x.size(0), -1)
        result = self.classification(feature)
        return result


if __name__ == "__main__":
    net = VGG('VGG16', 10)
    x = torch.randn(2, 3, 224, 224)
    y = net(x)
    print(y.size())
    print(net)

经过对VGGNet的学习，我们可以发现这些所谓的神经网络架构模型，其实就是卷积层+激活+池化等的组合，不同的就是要使用多少层卷积，每层卷积的卷积核数量、大小、步长等的区别，针对一些特定的数据集，如果你能设计出一个网络模型以更快的速度达到现有的更高的精度，那你就是开创者。

VGG16实现Cifar10分类

如果要把VGG16应用于Cifar10分类任务，那么上面提到的输入到全连接层的in_features需要修改，因为Cifar10的图片尺寸是3*32*32，经过全部卷积层后变成了1*1*512。

1
2
3
4
5
6
7
8
9
10
# 全连接层
self.classification = nn.Sequential(
    nn.Dropout(p=0.5),
    nn.Linear(in_features=512, out_features=512),
    nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(in_features=512, out_features=512),
    nn.ReLU(),
    nn.Linear(512, 10)
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# 训练(速度特别慢，5轮跑了十几个小时， 准确率76%，5轮后的损失还挺大的，其实还可以继续跑)
criterion = nn.CrossEntropyLoss()  # 定义损失函数 交叉熵
# 定义优化方法 随机梯度下降
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
for epoch in range(5):
    train_loss = 0.0
    for batch_idx, data in enumerate(cifar10.train_loader, 0):
        inputs, labels = data
        optimizer.zero_grad()  # 先将梯度设置为0

        out_puts = net(inputs)  # 将数据输入到网络
        loss = criterion(out_puts, labels)  # 计算损失

        loss.backward()
        optimizer.step()

        # 查看网络训练状态
        train_loss += loss.item()
        if batch_idx % 2000 == 1999:
            print(f'[{epoch+1}, {batch_idx+1}] loss {train_loss / 2000}')
            train_loss = 0.0
    print(f'Saving epoch {epoch+1} mode ...')
    state = {
        'net': net.state_dict(),
        'epoch': epoch+1
    }
    if not os.path.isdir('checkpoint'):
        os.mkdir('checkpoint')
    torch.save(state, f'./checkpoint/cifar10_epoch_{epoch+1}.ckpt')
print('Finished Training')

# 测试几个例子
check_point = torch.load('./checkpoint/cifar10_epoch_5.ckpt')
net.load_state_dict(check_point['net'])
start_epoch = check_point['epoch']
data_iter = iter(cifar10.test_loader)
test_image, test_labels = data_iter.next()
out_puts = net(test_image)
_, predict = torch.max(out_puts, 1)
print(predict)
print(test_labels)

# 批量计算整个测试集的预测效果
correct = 0
total = 0
with torch.no_grad():
    for data in cifar10.test_loader:
        images, labels = data
        out_puts = net(images)
        _, predicted = torch.max(out_puts.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
print(f'Accuracy of the network on the 10000 test images: {correct/total}')

这里介绍了保存训练模型和加载训练模型的方式。

使用VGG16模型训练速度较慢，因为网络结构较深；Cifar10的图片比较小，我尝试用了一个更简单的模型，达到的准确率与VGG16训练5轮的准确率差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class CNN(nn.Module):

    # 定义卷积神经网络需要的元素
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)  # 定义第一个卷积层
        self.pool1 = nn.MaxPool2d(2, 2)  # 池化层
        self.conv2 = nn.Conv2d(16, 64, kernel_size=3, padding=1)
        self.pool2 = nn.MaxPool2d(2, 2)
        self.conv3 = nn.Conv2d(64, 256, kernel_size=3, padding=1)
        self.pool3 = nn.MaxPool2d(2, 2)
        self.fc1 = nn.Linear(256*4*4, 512)  # 全连接层  这个输入值需要计算，根据输入图像的尺寸决定
        self.fc2 = nn.Linear(512, 128)      # 全连接层
        self.fc3 = nn.Linear(128, 10)       # 最后一个全连接层用作10分类
        self.dropout = nn.Dropout(p=0.5)

    def forward(self, _x):
        # 第一个卷积层首先经过ReLU做激活，然后池化
        feature = self.pool1(f.relu(self.conv1(_x)))
        # 第二个卷积层也先经过ReLU激活，然后池化
        feature = self.pool2(f.relu(self.conv2(feature)))
        feature = self.pool3(f.relu(self.conv3(feature)))
        # 对特征层Tensor维度进行变换
        feature = feature.view(_x.size(0), -1)
        # 特征层经过第一次全连接层操作，然后通过ReLU激活
        feature = f.relu(self.fc1(feature))
        self.dropout(feature)
        # 特征层经过第二次全连接层操作，然后通过ReLU激活
        feature = f.relu(self.fc2(feature))
        self.dropout(feature)
        # 特征层经过最后一次全连接层操作，得到最终要分类的结果（10分类标签）
        result = self.fc3(feature)
        return result