关联规则
啤酒与尿布的故事:
在美国,一些年轻的父亲下班后经常要到超市去买婴儿尿布,超市也因此发现了一个规律,在购买婴儿尿布的年轻的父亲们中,有30%~40%的人同时要买一些啤酒。超市随后调整了货架的摆放,将尿布和啤酒放在一起,因此,明显增加了销售额。
兴趣度度量
1、兴趣度度量的概念
挖掘出的模式(规律的表示形式)的简洁性、确定性和实用性即为兴趣度度量。
2、兴趣度度量的必要性
大量的数据 –> 挖掘出大量的规则 –> 规则一小部分是用户感兴趣的 –> 有必要进行兴趣度度量
3、兴趣度度量方法
简洁性度量:模式的便于人理解的度量
确定性度量:模式的可信性
方法:对于关联规则,确定性度量使用置信度。
设A和B为项目集合,A与B关联的规则A–>B的置信度定义为:
置信度(A–>B)= 同时包含A和B的元组数/包含A的元组数
举例:对某计算机商店购买物品的相关情况进行挖掘,得到一个置信度为85%的关联规则:
buys(X,”computer”) –> buys(X,”printer”)
意味着买计算机的顾客85%也买打印机。A的元组数为买计算机的事务数(顾客数),同时包含A和B的元组数为买计算机同时又买打印机的事务数(顾客数)。
实用性度量:模式的有用性
方法:对于关联规则,实用性度量使用支持度。
设A和B为项目集合,A与B关联的规则A”B的支持度定义为:
支持度(A–>B)= 同时包含A和B的元组数/元组总数
举例:对某计算机商店购买物品的相关情况进行挖掘,得到一个支持度为30%的关联规则:
buys(X,”computer”) –> buys(X,”printer”)
意味着该计算机商店的所有顾客的30%同时购买了计算机和打印机。元组总数为购买计算机或购买打印机的事务数(顾客数),同时包含A和B的元组数为买计算机同时又买打印机的事务数(顾客数)。
注意
- 同时满足用户定义的最小置信度阈值和最小支持度阈值的关联规则称为强关联规则,并认为是有趣的。
- 置信度太低,说明关联规则的可信度差;支持度太低,说明关联规则不具有一般性,即有用性差。
- 关联规则表示:buys(X,”computer”) “ buys(X,”printer”) [30%,85%]
关联规则挖掘的基本概念
定义3-1 关联规则挖掘的数据集记为D(一般称为事务数据库),
D={t1,t2,t3……,tk, ……tn},tk={i1,i2,…,im…ip},
tk (k=1,2,….n)称为事务,im (m=1,2,…p)称为项目。
定义3-2 设I={i1,i2….im}是D中全体项目组成的集合,I的任何子集X称为D中的项目集,|X|=k称集合X为k项目集。设tk和X分别为D中的事务和项目集,如果X ⊆ tk,称事务tk包含项目集X。每一个事务都有一个惟一的标识符,称为TID。
定义3-3 数据集D中包含项目集X的事务数称为项目集X的支持数,记为Ϭx。项目集X的支持度记为support(X):
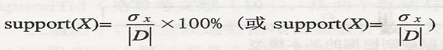
其中|D|是数据集D的事务数,若support(X)不小于用户指定的最小支持度,则称X为频繁项目集,简称频集(或大项目集),否则则称X为非频繁项目集,简称非频集(或小项目集)。
针对以上定义举个例子来简单说明下:
| T1 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| T2 | 2 | 3 | 4 | 5 |
| T3 | 2 | 3 | 5 | 6 |
以上表格可以简称为D数据集(也是一个事务数据库),每一行就是一个事务(t),T1、T2是事务的唯一标识。
假设项目集x={2, 3},则|x|=σx=3(在3个事务中都有出现)
假设项目集y={2, 3, 4},则|y|= σy=2(在2个事务中出现过)
定理3-1 设X、Y是数据集D中的项目集:
(1) 若X ⊆ Y ,则support(X) ≥support(Y)
(2) 若X ⊆ Y ,如果X是非频集,则Y也是非频集。
(3) 若X ⊆ Y,若Y是频集,则X也是频集。
定义3-4 若X、Y为项目集,且X∩Y = Ø,蕴含式X=>Y称为关联规则,X、Y分别称为关联规则X=>Y的前提和结论。项目集X∪Y的支持度称为关联规则的X=>Y的支持度,记作:support(X=>Y),support(X=>Y)=support(X∪Y)
关联规则X=>Y的置信度记作,confidence(X=>Y):
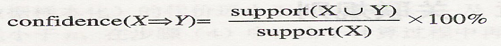
通常用户根据挖掘需要要指定的最小置信度记为minconfidence。支持度和置信度是描述关联规则的两个重要的概念,前者用于衡量关联规则在整个数据集中的统计重要性,后者用于衡量关联规则的可信程度。
定义3-5 若support(X=>Y) ≥ minsupport,且confidence(X=>Y) ≥ minconfidence,称关联规则X=>Y为强规则,否则称弱规则。
关联规则挖掘的任务就是挖掘出D中所有的强规则。强规则X=>Y对应的项目集(X ∪Y)必定是频集,频集(X∪ Y)导出的关联规则X=>Y的置信度可由频集X和(X∪ Y)的支持度计算。因此把关联规则挖掘分为以下两个子问题:
(1)根据最小支持度找出数据集D中的所有频集。
(2)根据频繁项目集和最小置信度产生关联规则。
关联规则种类
1、布尔关联规则
如果考虑事务的项集中的项存在与不存在,而得出的关联规则称为布尔关联规则。
2、单维与多维关联规则
如果规则A–>B中,项集A或B都是一维谓词的表达式,则该规则为单维规则,否则为多维规则。如:
buys(x,computer) –> buys(x,printer)
age(x,30-39)^income(x,42k-48k) –> buys(x,computer)
3、单层和多层关联规则
例如:下层概念的青岛啤酒和帮宝适尿布之间的关联规则不如上层概念的啤酒和尿布之间的关联规则对促销指导有作用。这就是涉及多个概念层的关联规则。
关联规则算法——Apriori算法
Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。
Apriori使用一种称作逐层搜索的迭代方法,k-项集用于探索(k+1)-项集。首先找出频繁1-项集的集合。称为集合L1。L1用于找频繁2-项集的集合L2,而L2用于找L3,如此下去直到不能找到频繁k-项集。
为了提高频繁项集逐层产生的效率,一种称作Apriori性质的重要性质用于压缩搜索空间
Apriori性质:如果项目集X 是频繁项目集,那么它的所有非空子集都是频繁项目集
利用L(k-1) 找到Lk的过程由连接和剪枝组成:
(1)连接步:为找Lk,通过L(k-1)与自己连接产生候选k-项集的集合。该候选项集的集合记为Ck。设l1和l2是L(k-1)中的项集。记号为li[j]表示li的第j项。为方便计,假定事务或项集中的项按字典次序排序。执行连接L(k-1)∞L(k-1),其中L(k-1)的元素是可连接的。连接L1项集和L2项集产生的结果是项集l1[1]l2[2]………l1[k-1]l2[k-1].
(2)剪枝步:Ck是Lk的超集;即是,它的成员可以是也可以不是频集,但所有频集k-项集都包含在Ck中。扫描数据库,确定Ck中每个候选的计数,从而确定Lk。然而,Ck可能很大,这样所涉及的计算量就很大。为压缩Ck,可以利用以下办法使用Apriori性质:任何非频集的(k-1)-项集都不可能是频繁k-项集的子集。因此,如果一个候选k-项集的(k-1)-子集不在Lk-1中,则该候选也不可能是频繁的,从而可以有Ck中删除。
使用Apriori算法解决例题
例:该例数据库中有9个事务,即|D|=9。Apriori假定事务中的项按字典次序存放。

最小支持度计数为2,最小置信度为70%。
解答:
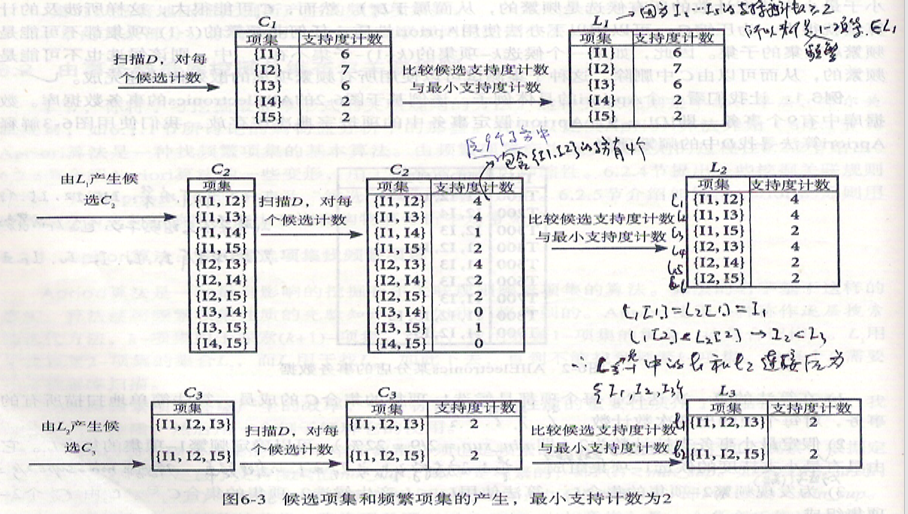
1)在算法的第一次迭代,每个项集都是候选1-项集的集合C1的成员。算法简单的扫描所有的事务,对每个项的出现次数计数。
2)假定最小事务支持数为2(即min_sup = 2/9)。可以确定频繁1-项集的集合L1.它由具有最小支持度的候选1-项集组成。
3)为发现频繁2-项集的集合L2,算法使用L1∞L1产生候选2-项集的集合C2.
4)下一步,扫描D中的事务,计算C2中每个候选项集的支持计数。
5)确定频繁2-项集的集合L2,它由最小支持度的C2中的候选2-项集组成。
6)候选3-项集的集合C3的产生详细地产生过程如下图所示。
注意:L2与L2做连接时,只有前缀相同的才能做连接,例如{I1, I2}与{I1, I3}连接得到{I1, I2, I3};
{I2, I3}与{I2, I4}连接得到{I2, I3, I4}。但是{I1, I2}与{I2, I3}不能做连接。(据我观察,实际做连接也可以,一般得到的结果都是重复的或者会被剪枝掉)

首先,令
1 | C3=L2∞L2={{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5} } |
根据Apriori性质,频繁项集的所有子集必须是频繁的,我们可以确定后4个不是频繁的。因此可以将其从C1删除。这样在此后扫描D确定L3时就不必再求它们的计数值。
7)扫描D中的事务,以确定L3,它由具有最小支持度的C3中的候选3-项集组成。
8)算法使用L3∞L3产生候选4-项集的集合C4。尽管产生了{I1,I2,I3,I5},这个项集被剪去,因为它的子集{I2,I3,I5}不是频繁的。这样,C4 = Ø,因此算法结束,找出了所有的频繁项集。
一旦由数据库D中的事务找出频繁项集,由它们产生的强关联规则是直接的。这里,
频繁集L1={I1, I2, I5},L1的非空子集有{I1, I2}, {I1, I5}, {I2, I5}, {I1}, {I2}, {I5}
I1^ I2 => I5, confidence=2/4=50%
I1 ^ I5 => I2, confidence=2/2=100 %
I2 ^ I5 => I1, confidence=2/2=100 %
I1 => I2 ^ I5, confidence=2/6=33 %
I2 => I1 ^ I5, confidence=2/7=29 %
I5 => I1 ^ I2, confidence=2/2=100 %
最小置信度阀值为70%,则只有第2、3和最后一个规则可以输出。
频繁集L2={I1, I2, I3},L2的非空子集有{I1, I2}, {I1, I3}, {I2, I3}, {I1}, {I2}, {I3}
I1^ I2 => I3, confidence=2/4=50%
I1 ^ I3 => I2, confidence=2/4=50 %
I2 ^ I3 => I1, confidence=2/4=50%
I1 => I2 ^ I3, confidence=2/6=33 %
I2 => I1 ^ I3, confidence=2/7=29 %
I3 => I1 ^ I2, confidence=2/6=33 %
无满足情况的。