贝叶斯分类(朴素)
• 是一种统计学分类方法
• 可以用来对一个未知的样本判定其属于特定类的概率
• 分类模型是在有指导的学习下获得
• 分类算法可与决策树和神经网络算法媲美
• 用于大型数据库时具有较高的分类准确率和高效率。
基础概念
朴素贝叶斯分类的假设前提:类别C确定的情况下,不同属性(X1,X2)间是相互独立的,即条件独立。(朴素即为条件独立)
即:C确定下,P(X1,X2)=P(X1)P(X2) ;或表示为:P(X1,X2|C)=P(X1|C)P(X2|C)
设X是未知类别的数据样本(属性值已知),H为假定:X属于某特定类的类C。分类问题即为,确定P(H|X)——给定观测数据样本X,假定H成立的概率。
后验概率:P(H|X),在条件X下,H的后验概率
先验概率:P(H)
贝叶斯定理
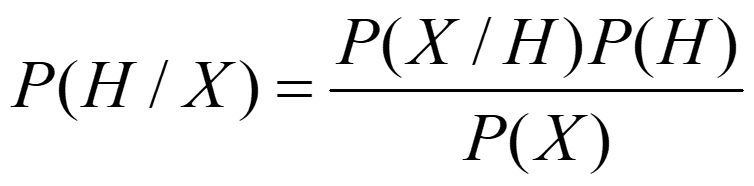
注:P(X/H)相当于已知带标签的数据,即有导师了。
换个表达形式就会明朗很多:
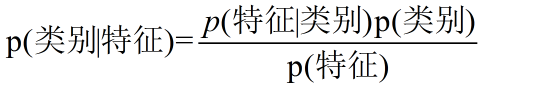
贝叶斯分类过程
假定有m个类别,C1,C2,……,Cm。根据一个未知的数据样本X(即没有类标号),分类法将预测X属于具有最高后验概率(条件X下)的类。即,朴素贝叶斯分类器将未知的样本分配给类Ci,当且仅当:P(Ci|X) > P(Cj|X), 1<=j<=m,j≠i
根据贝叶斯定理:P(Ci|X) = P(X|Ci)*P(Ci)/P(X)
由于P(X)对所有类别为常数(也就是训练样本中,X特征的样本数量占总样本的比例)
只需要 P(X|Ci)*P(Ci) 最大即可。
如果类的先验概率未知,则通常假设这些类是等概率的,即P(C1)=P(C2)=……=P(Cm),并据此对P(X|Ci)最大化,否则最大化P(X|Ci)*P(Ci)。
注意,类的后验概率可以用P(Ct) = St/S计算,其中St是类别Ct在训练样本中的数量,S是训练样本总数。
给定具有许多属性的数据集,计算P(X|Ci)的开销可能非常大,为降低计算P(X|Ci)的开销,可以做类条件独立的朴素假定。给定样本的类别号,假定属性值相互条件独立,即在属性间不存在依赖关系,那就可以这样来计算
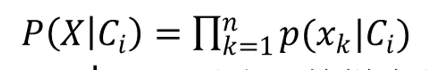
概率P(x1|Ci)、P(x2|Ci)、……、P(xn|Ci)可由训练样本估值,其中
如果Ak是离散属性,则
P(xk|Ci)=sn/si,其中sn是Ak属性上,属性值为xk的类Ci的训练样本数,si是类为Ci的训练样本数。如果Ak是连续值属性,则通常假定该属性服从高斯分布:
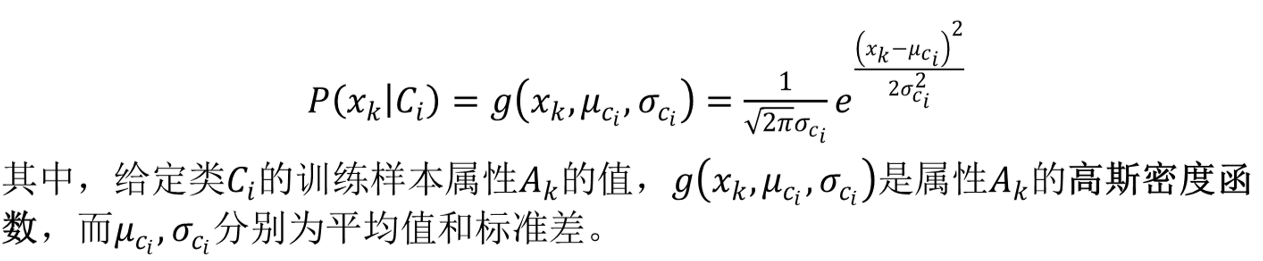
为对未知样本X分类,对每个类Ci,计算P(X|Ci)P(Ci)。样本X被分配到类别Ci,当且仅当:
P(X|Ci)P(Ci) > P(X|Cj)P(Cj),1<=j<=m,j≠i
换言之,X被指派到其P(X|Ci)P(Ci)最大的Ci。
理论上讲,贝叶斯分类具有最小的出错率,然而实践中并非总是如此,这是由于其应用的假定(如类条件独立性)的不准确性,以及缺乏可用的概率数据造成的。
拉普拉斯校正法
问题:如果某个P(xk|Ci)概率值为零,会发生什么?
导致这个Ci的概率值为0。
解决办法:
拉普拉斯校准法:给未出现的情况+1,注意其他出现的情况也都要+1,且总数也要求和。
举例:

贝叶斯分类例题
下表由雇员数据库的训练数据组成,数据已泛化。例如,age”31……35”表示年龄在31~35之间。对于给定的行,count表示该行具有特定值的元组数。
| department | status | age | salary | count |
|---|---|---|---|---|
| sales | senior | 31……35 | 46K……50K | 30 |
| sales | junior | 26……30 | 26K……30K | 40 |
| sales | junior | 31……35 | 31K……35K | 40 |
| systems | junior | 21……25 | 46K……50K | 20 |
| systems | senior | 31……35 | 66K……70K | 5 |
| systems | junior | 26……30 | 46K……50K | 3 |
| systems | senior | 41……45 | 66K……70K | 3 |
| marketing | senior | 36……40 | 46K……50K | 10 |
| marketing | junior | 31……35 | 41K……45K | 4 |
| secretary | senior | 46……50 | 36K……40K | 4 |
| secretary | junior | 26……30 | 26K……30K | 6 |
给定一个数据元组,它在属性department,age,salary的值分别为”system”,”26……30”和”46K……50K”,该元组status的朴素贝叶斯分类是什么?
解答:
假设X={department=system, age=26……30, salary=46K……50K}
P(C|X) = P(X|C)P(C)/P(X)
P(X)是固定的不用算,只要计算P(X|C)P(C)最大即可。
总记录数为52+113=165,
假设senior和junior对应的类别分别为C1,C2,则P(C1)=52/165,P(C2)=113/165
P(X|C1) = P(department=system|C1) x P(age=26……30|C1) x P(salary=46K……50K|C1)
= [(5+3) / 52] x (0/52) x [(30+10)/52]
因为这里的P(age=26……30|C1)=0,所以需要使用拉普拉斯校正,给senior对应的每一个年龄段样本数+1,从21~50共有6个年龄段,所以P(age=26……30|C1)=1/58;
P(X|C1) = 0.154 x 0.017 x 0.769 = 0.002
P(X|C2) = P(department=system|C2) x P(age=26……30|C2) x P(salary=46K……50K|C2)
= (20+3)/113 x (40+3+6) x (20+3)/113
= 0.204 x 0.434 x 0.204 = 0.018
P(X|C1)P(C1) = 0.002 x 0.315 = 0.00063
P(X|C2)P(C2) = 0.018 x 0.685 = 0.01233
因为P(X|C2)P(C2) > P(X|C1)P(C1),所以该元组status的朴素贝叶斯分类是junior。