感知机与BP算法
M-P 神经元模型 [McCulloch and Pitts, 1943]
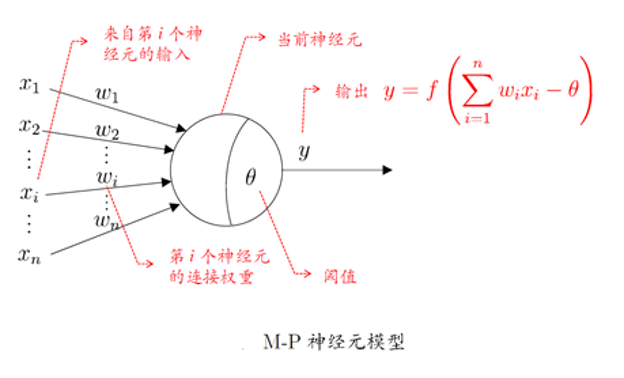
输入:来自其他n个神经元传递过来的输入信号(特征值)
处理:输入信号通过带权重的连接进行传递, 神经元接受到总输入值将与神经元的阈值进行比较
输出:通过激活函数的处理以得到输出
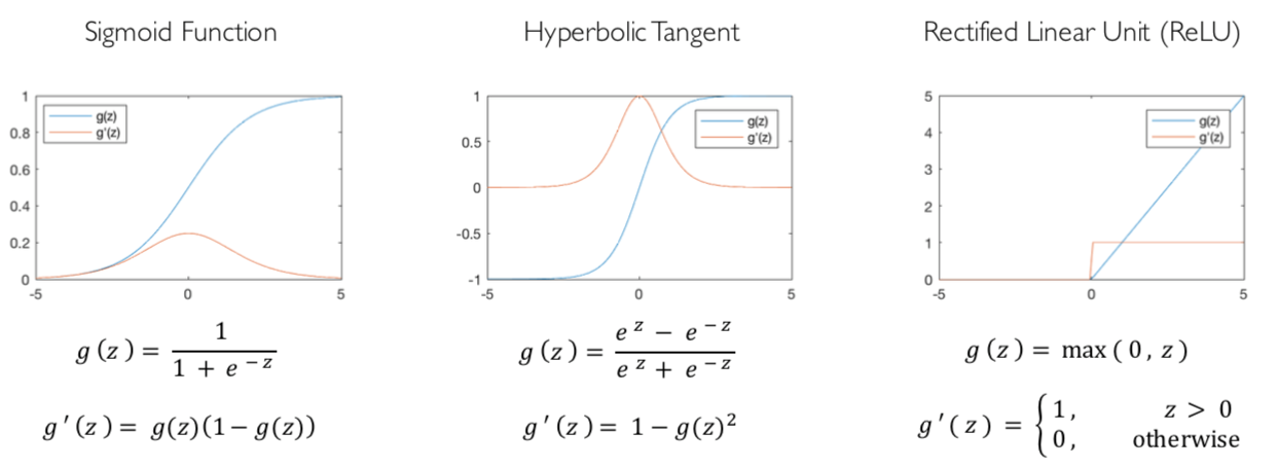
激活函数
感知机
单层感知机(又叫单层前馈网络)
两个输入神经元的感知机网络结构示意图
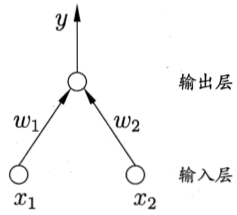
感知机(Perceptron)由两层神经元组成, 输入层接受外界输入信号传递给输出层, 输出层是一个或多个M-P神经元(亦称阈值逻辑单元,threshold logic unit)
感知机能够容易地实现逻辑与、或、非运算,针对上面的感知机网络结构图,假设激活函数为跃迁函数,f(x) = 1, x>=0;f(x) = 0, x<0。
与运算:令w1 = w2 = 1, Θ=2,则y = f(1*x1+1*x2-2)
在x1 = x2 = 1时,y = 1;在x1 = 0, x2 = 1时,y = 0
或运算:令w1 = w2 = 1, Θ=0.5,则y = f(1*x1+1*x2-0.5)
在x1 = 1或x2 = 1时,y = 1
非运算:令w1 = -0.6, w2 = 0, Θ=-0.5,则y = f(-0.6*x1+0.5)
在x1 = 1时,y = 0;在x2 = 0时,y = 1
事实上,上述与、或、非问题都是线性可分(linearly separable)的问题,可以证明,若两类模式是线性可分的,即存在一个线性超平面能将它们分开,则感知机的学习过程一定会收敛而求得适当的权向量w;否则感知机学习过程将会发生振荡,w难以稳定下来,不能求得合适解,例如感知机甚至不能解决异或这样简单的非线性可分问题。
Minsky & Papert (1969) 《Perceptron》感知器无法解决对XOR(异或)这样的分类任务
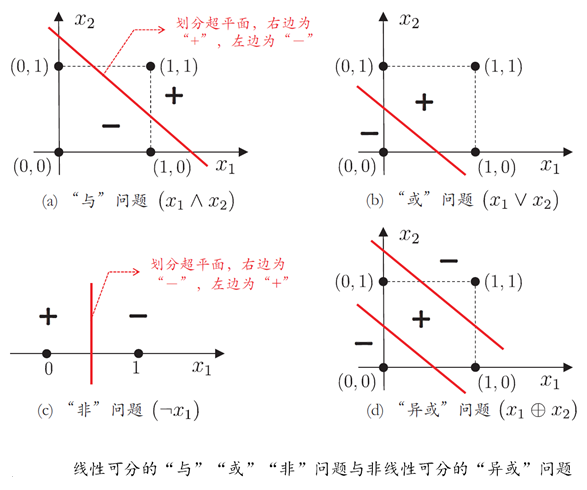
上面这个图的数据集仅是四个点,不是平面上所有的点
要解决非线性可分问题,需考虑多层功能神经元,如下图这个简单的两层感知机就能解决异或问题。在该图中,输出层和输入层之间的一层神经元,被称为隐层或隐含层,隐含层和输出层神经元都是有激活函数的功能神经元。
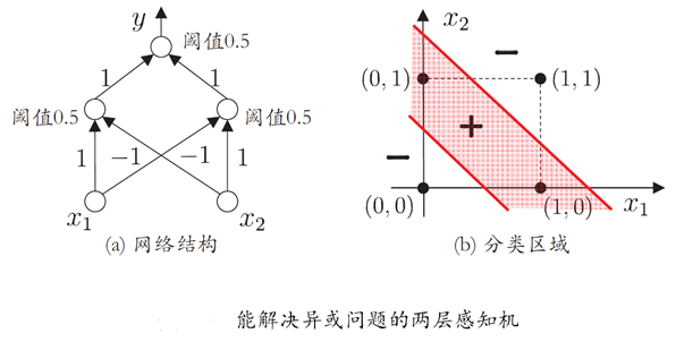
x1 = 1, x2 = 1, y = 0 ; x1 = 1, x2 = 0, y = 1
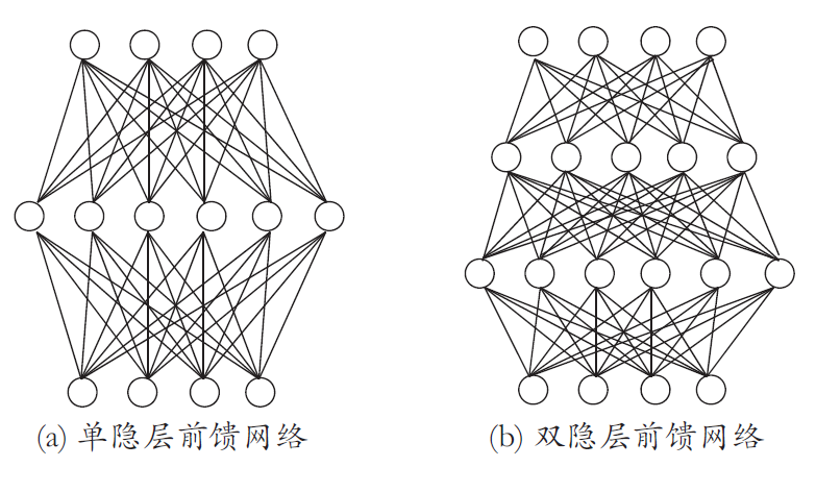
多层前馈神经网络
根据上面的两层感知机问题,可以得到更一般的多层前馈神经网络
定义:每层神经元与下一层神经元全互联, 神经元之间不存在同层连接也不存在跨层连接
前馈:输入层接受外界输入, 隐含层与输出层神经元对信号进行加工, 最终结果由输出层神经元输出
学习:根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的“阈值”
前馈并不意味着网络中的信号不能向后传,而是指网络拓扑结构上不存在环或回路
神经网络的表示能力
万能近似定理
只需要一个包含足够多神经元的隐层, 多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数[Hornik et al. , 1989]
误差反向传播算法(Error BackPropagation)
BP算法是最成功的训练多层前馈神经网络的学习算法,关于手动推导误差反向传播算法的过程,前面转发了一篇文章,手动推导BP算法。这里主要从例子来体验这一过程。
参数优化
BP是一个迭代学习算法, 在迭代的每一轮中对参数进行一次更新估计
前向计算
step1: 计算隐层的神经元
step2: 计算输出层的神经元
step3: 计算误差
网络参数
参数包括:权重,阈值
网络训练的过程就是参数优化的过程
反向计算
step1: 计算输出层的梯度
step2: 从输出层开始,循环直到最早的隐藏层
2.1: 将误差传播回前一层
2.2: 更新这两层间的权重与阈值
例题1:
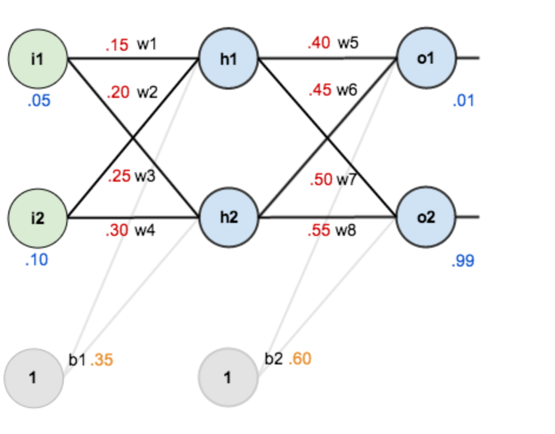
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近;激活函数为sigmoid函数。
Step1 前向传播
1.输入层—->隐含层:
计算神经元h1的输入加权和:
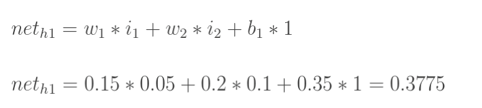
神经元h1的输出o1:
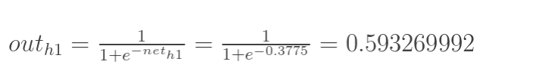
同理,可计算出神经元h2的输出o2:
out(h2) = 0.596884378
2.隐含层—->输出层:
[0.75136079 , 0.772928465]
Step2 反向传播
1.计算总误差:

分别计算o1和o2的误差,总误差为两者之和:

2.隐含层—->输出层的权值更新
以权重参数w5为例,如果想知道w5对整体误差产生了多少影响,计算整体误差E(total)对w5的偏导值,根据链式法则:
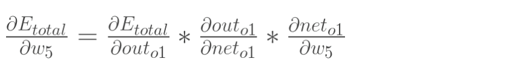
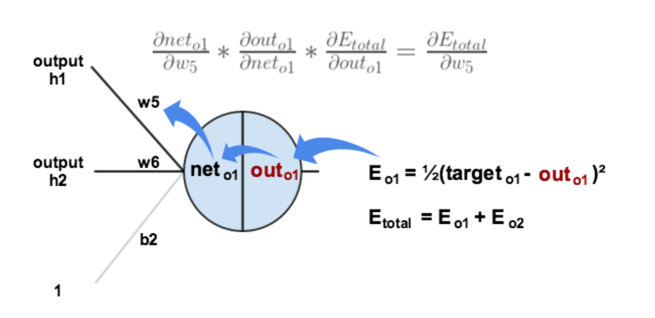
根据下图可以直观的看清楚误差是如何反向传播的
现在我们来分别计算每个式子的值:
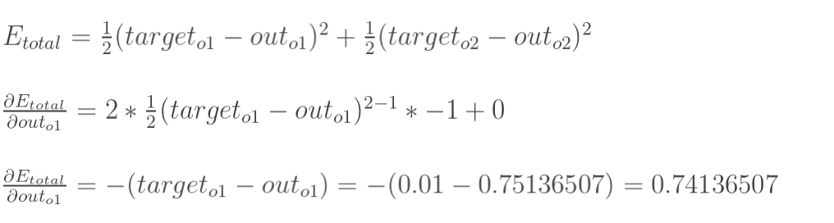

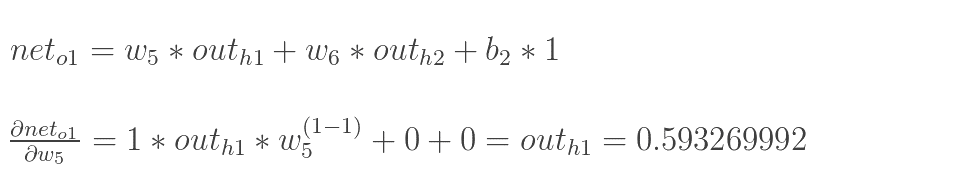

更新w5的值:(学习速率这里取0.5)
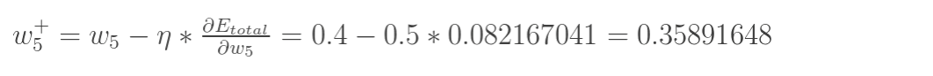
同理,可更新其它参数w6,w7,w8,……
这里E对w5的偏导实际上是:
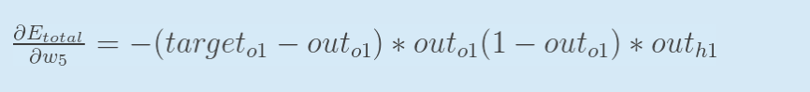
这个式子有助于我们推导出一般性的结论,下面会讲。
3.隐含层—->隐含层的权值更新:
以权重参数w1为例,如果想知道w1对整体误差产生了多少影响,计算整体误差E(total)对w1的偏导值,根据链式法则
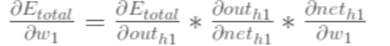
计算的过程与之前的类似,不同之处:隐含层之间的权值更新时,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。

反向传播公式推导
§在单个样本上的平方误差定义为:
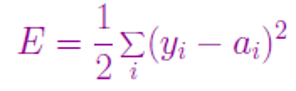
其中,求和是对输出层的所有节点进行的;yi是真值,ai是预测值,ai=g(in(i))= g(ΣWjiaj)
g是激活函数,Wji是从前一层的第j个神经元到输出层i神经元的权重。
输出层的权值更新:
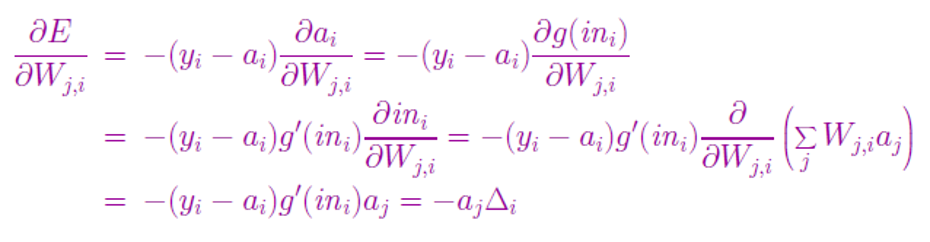
这个推导的结果和上面的E对W5的偏导结果式子(蓝色字体)是一致的。把这里的▲i记为修正误差。
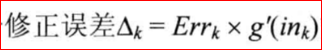
所以说如果要求E对w6的偏导,只需要把aj从out(h1)改为out(h2)即可。
隐藏层的权值更新:
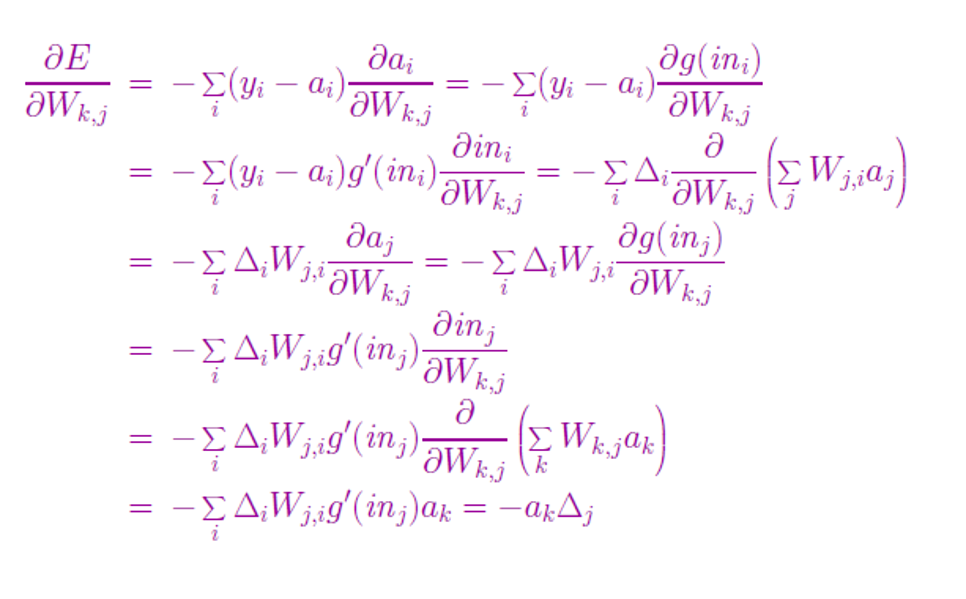
例题2:
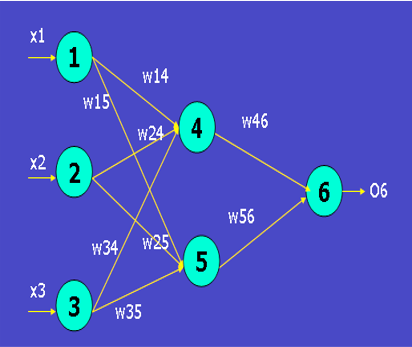
训练样本x={1,0,1},类标号(标签)为1,激活函数为sigmoid函数
| X1 | X2 | X3 | θ4 | θ5 | θ6 | W14 |
|---|---|---|---|---|---|---|
| 1 | 0 | 1 | -0.4 | 0.2 | 0.1 | 0.2 |
| W15 | W24 | W25 | W34 | W35 | W46 | W56 |
| -0.3 | 0.4 | 0.1 | -0.5 | 0.2 | -0.3 | -0.2 |
step2 前向传播
| 神经元 | 输入 net | 输出o |
|---|---|---|
| 4 | 0.2*1+0.4*0+(-0.5)*1-0.4=-0.7 | 1/(1+e-(-0.7))=0.332 |
| 5 | (-0.3)*1+0.1*0+(0.2)*1-(-0.2)=0.1 | 1/(1+e(-0.1))=0.525 |
| 6 | (-0.3)*0.332+(-0.2)*0.525-(-0.1)=-0.105 | 1/(1+e-(-0.105))=0.474 |
step2 反向传播
2.1 计算修正误差
| 神经元 | 修正误差 |
|---|---|
| 6 | (1-0.474)*0.474*(1-0.474) =0.1311 |
| 5 | (0.1311*(-0.2))*0.525*(1-0.525)=-0.0065 |
| 4 | (0.1311*(-0.3))*0.332*(1-0.332)=-0.0087 |
输出层修正误差:Err(k) = Ok*(1-Ok)*(T-Ok)(T是标签输出)
隐含层修正误差:Err(j) = Oj*(1-Oj) *( Σ( Err(k) * W(jk) )(与所有输出相关联的地方都要计算,这里因为只有一个输出所以比较容易积善)
2.2 计算权重和阈值的更新(学习率α,此处取值为0.9)
| w46 | -0.3+0.9*0.332*0.1311=-0.216 |
|---|---|
| w56 | -0.2+0.9*0.525*0.1311=-0.138 |
| w14 | 0.2+0.9*1*(-0.0087)=0.192 |
| w15 | -0.3+0.9*1*(-0.0065) =-0.306 |
| w24 | 0.4+0.9*0*(-0.0087)=0.4 |
| w25 | 0.1+0.90\(0.0065)=0.1 |
| w34 | -0.5+0.9*1*(-0.0087)=-0.508 |
| w35 | 0.2+0.9*1*(-0.0065)=-0.194 |
| Ө6 | 0.1+0.9*0.1311=0.218 |
| Ө5 | 0.2+0.9*(-0.0065)=0.194 |
| Ө4 | -0.4+0.9*(-0.0087)=-0.408 |
这里偏置的更新公式为: θj = θj + α*Err(j)
深度学习
多层前馈网络局限
神经网络由于强大的表示能力, 经常遭遇过拟合, 表现为:训练误差持续降低, 但测试误差却可能上升
如何设置隐层神经元的个数仍然是个未决问题. 实际应用中通常使用“试错法”调整
缓解过拟合的策略
早停:在训练过程中, 若训练误差降低, 但验证误差升高, 则停止训练
正则化:在误差目标函数中增加一项描述网络复杂程度的部分, 例如连接权值与阈值的平方和
2006年,Hinton在《Science》上发表了论文,首次提出了“深度信念网络”的概念。
与传统的训练方式不同,“深度信念网络”有一个“预训练”(pre-training)+“微调”(fine-tuning)技术来对整个网络进行优化训练。
他给多层神经网络相关的学习方法赋予了一个新名词–“深度学习”。
增加隐层的数目比增加隐层神经元的数目更有效。这是因为增加隐层数不仅增加了拥有激活函数的神经元数目, 还增加了激活函数嵌套的层数.