无监督学习–聚类算法
聚类算法是一种无监督学习算法,监督学习指的是我们的训练数据有一系列标签,我们通过假设函数去拟合它,而在无监督学习中,我们的数据不带有任何标签
聚类的定义
将物理或抽象的对象的集合分组成为由类似的对象组成的多个类的过程被称为聚类。 同一类中的对象之间具有较高的相似度,而不同类中的对象差别较大。
注:相似度是基于描述对象的属性计算的,计算是对对象之间距离进行计算
基于划分的方法–K-means聚类

例题
下表密度和含糖率为西瓜两个属性,按两属性对西瓜聚类
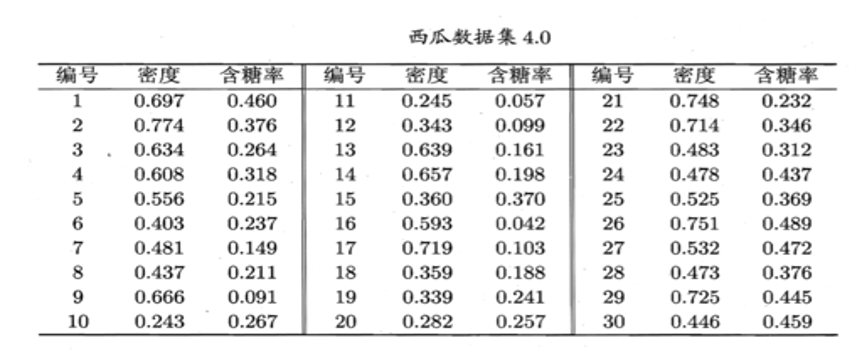
假定聚类簇数 k= 3, 算法开始时随机选取三个样本x_6,x_12,x_24作为初始均值向量,
即:μ1=(0.403;0.237),μ2=(0.343;0.099),μ3=(0.478;0.437).
算法第一步是要进行簇分配
考察样本x1=(0.697;0.460),它与当前均值向量μ1,μ2,μ3的距离(欧几里得距离)分别为 0.369, 0.506, 0.166,因此x1将被划入簇C3中.
类似的,对数据集中的所有样本考察一遍后,可得当前簇划分为
C1={x3,x5,x6,x7,x8,x9,x10,x13,x14,x17,x18,x19,x20,x23}
C2={x11,x12,x16 }
C3={x_1,x_2,x_4,x_15,x_21,x_22,x_24,x_25,x_26,x_27,x_28,x_29,x_30}
算法第二步移动聚类中心
于是,可从C1、C2、C3分别求出新的均值向量:
μ1′=(0.473;0.207),μ2′=(0.394;0.066),μ3′=(0.602;0.396)
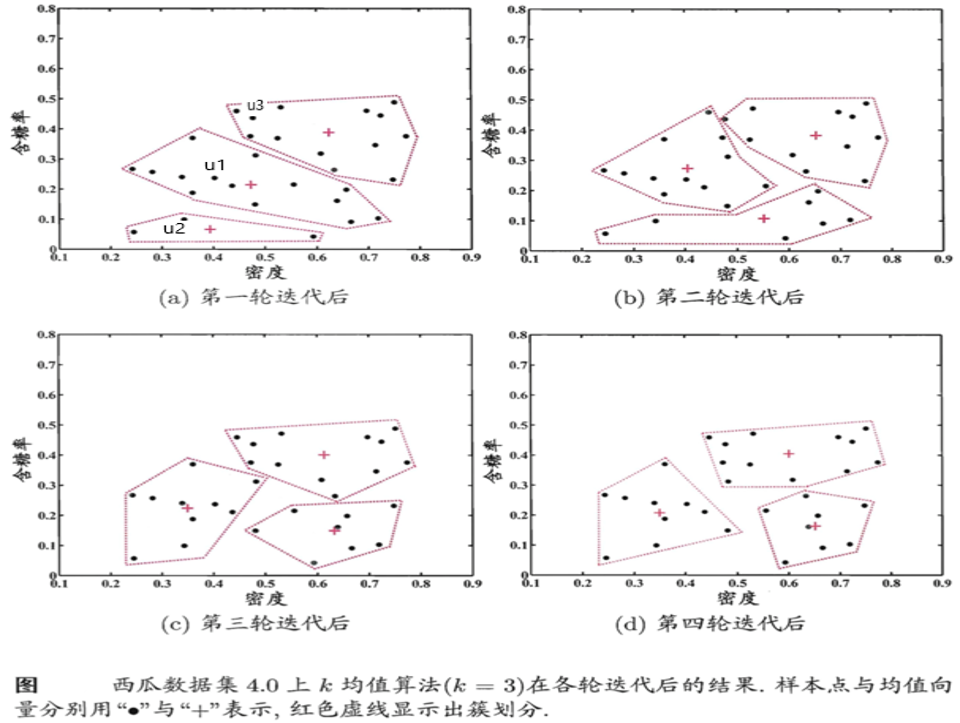
更新当前均值向量后,不断重复上述过程,如下图所示,第五轮迭代产生的结果与第四轮迭代相同,于是算法停止,得到最终的簇划分。
k-平均法算法分析
复杂度:计算复杂度是O(nkt),其中,n是所有对象的数目,k是簇的数目,t是迭代的次数。通常地,k<<n,且t<<n。这个算法经常以局部最优结束。
优缺点:
• 优点:当划分结果簇是密集的,而簇与簇之间区别明显时,它的效果较好。对处理大数据集,该算法是相对可伸缩的和高效率的.
• 缺点:
①k-平均方法只有在簇的平均值被定义的情况下才能使用。这可能不适用于某些应用,例如涉及有分类属性的数据。
②要求用户必须事先给出k(要生成的簇的数目)可以算是该方法的一个缺点,因为K比较难确定。
③k-平均值方法不适合于发现非凸面形状的簇,或者大小差别很大的簇。
④对于“噪声”和孤立点数据是敏感的,少量的该类数据能够对平均值产生极大的影响。
基于划分的方法–k-mediods聚类
k-中心点法产生原因: k-平均法对孤立点过于敏感。
k-中心点法工作原理:划分基于标准绝对误差最小化的原则进行。标准绝对误差定义:
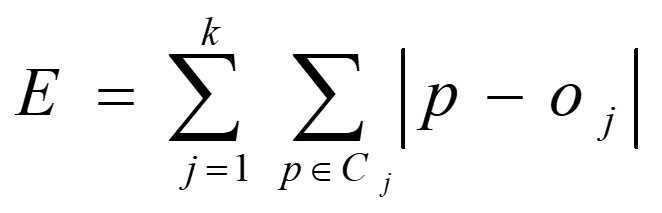
E是数据集中所有对象绝对误差之和;p是空间中点,代表簇Cj中的一个给定的对象;oj是簇Cj中的代表对象(即oj代表了Cj,注意代表对象是某个样本点)。通常,该算法重复迭代,直到每个代表对象都成为它的簇的实际中心点。
新代表对象选择策略(迭代策略)
首先为每个簇随意选择一个代表对象;剩余的对象根据其与代表对象的距离分配给最近的一个簇。然后反复地用非代表对象来替代代表对象,以改进聚类的质量。
到目前为止好像k-中心点法与k-均值法没啥区别,就是误差定义进行了修改,然后实际上的核心点是上面的最后一句改进聚类质量.
聚类质量的判定方法
聚类质量用一个代价函数来估算,该函数度量对象与其代表对象之间的相异度。
为了判定一个非代表对象
Orandom是否是当前一个代表对象Oj的好的替代,k-中心点法为所有非中心点对象p设置一个代价变量Cpjr,Cpjr分下面的四种情况被定义:
p当前隶属于中心点对象
Oj。如果Oj被Orandom所代替作为中心点,且p离一个Oi最近,i≠j,那么p被重新分配给OiCpjr=d(p,Oi )-d( p,Oj )>=0p当前隶属于中心点对象
Oj。如果Oj被Orandom代替作为一个中心点,且p离Orandom最近,那么p被重新分配给OrandomCpjr=d(p, Orandom )-d( p,Oj )<0p当前隶属于中心点
Oi,i≠j。如果Oj被Orandom代替作为一个中心点,而p仍然离Oi最近,那么对象的隶属不发生变化。Cpjr=0p当前隶属于中心点
Oi,i≠j。如果Oj被Orandom代替作为一个中心点,且p离Orandom最近,那么p被重新分配给OrandomCpjr=d(p, Orandom )-d( p,Oi)<0
下面这张图可以比较清晰的描述这四种情况
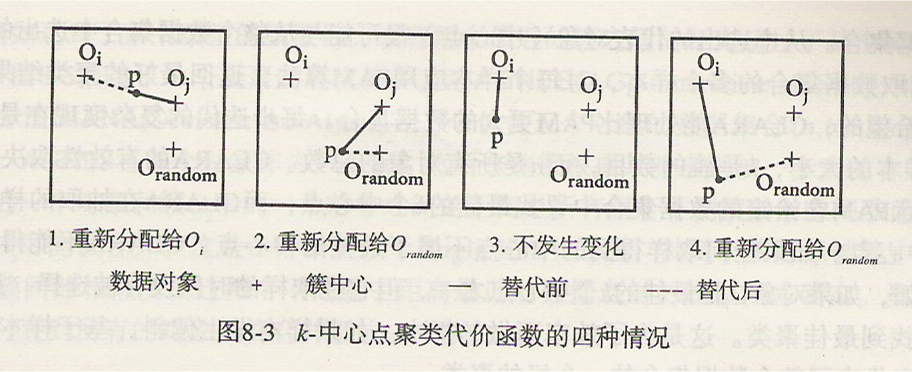
对于替换产生代价的理解:
假设两个类,中心点分别为Oi和Oj,其标准误差为E1,现在Oj被Orandom替代,替代后就只有一个对象p从隶属Oj类归到了Oi类(其他的对象都没移动,即所属类都没变化),这时E1中d( p,Oj )不存在了(因为p不在这个类里了),而Oi类里面多了d(p,Oi ),而且d(p,Oi )>d( p,Oj ),所以计算新的E2时,E2>E1,这说明这次调整不成功。从代价函数角度来看,这个意思就是Cpjr>0,即这次调整是不值得的。
注意E的计算公式就是d(p,Oi)(这里定义d是曼哈顿距离的话)。
替代的总代价(S=∑ Cpjr )是所有非中心点对象所产生的代价之和。如果总代价是负的,那么标准绝对误差将会减小, Oj可以被Orandom替代。如果总代价是正的,则当前的中心点Oj被认为是可接受的,在本次迭代中没有变化发生。
与K-means算法一样,K-medoids也是采用欧几里得距离来衡量某个样本点到底是属于哪个类簇。终止条件是,当所有的类簇的质点都不在发生变化时,即认为聚类结束。
该算法除了改善K-means的“噪声”敏感以后,其他缺点和K-means一致,并且由于采用新的质点计算规则,也使得算法的时间复杂度上升为:每次迭代O(k(n-k)^2)
总结K-中心点算法步骤:
输入:包含n个对象的数据库和簇数目k;
输出:k个簇
随机选择k个代表对象作为初始的中心点
将每个剩余对象分配到最近的中心点所代表的簇
随机地选择一个非中心点对象y
计算每个对象P用
Orandom代替中心点Oj的总代价s= ∑Cpjr如果s为负,则可代替,形成新的中心点
重复(2)(3)(4)(5),直到k个中心点不再发生变化。
基于层次的方法
最短距离法
类间距离定义:两类中最近元素之间距离。

类间距离
1 | d{1, 2, 3, 4}{5, 6, 7} |
以类间距离为聚类依据,依次逐次选择类间最短距离进行聚类的过程叫最短距离聚类法。
假定5个对象间的距离如下表所示,试用最短距离法聚类并画出树形图(Dendrogram)。
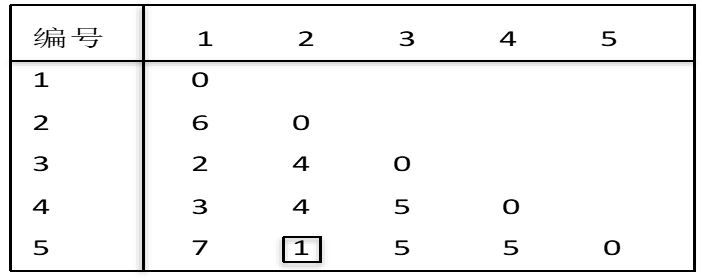
解:先将五个对象都分别看成是一个类,由上表看到,最靠近的两个类是2和5,因为它们具有最小类间距离
min{6, 2, 3, 7, 4, 4,1, 5, 5, 5}=d25=1
将2和5合并为一个新类{2,5}。第一次聚类后,各类之间距离如下表:
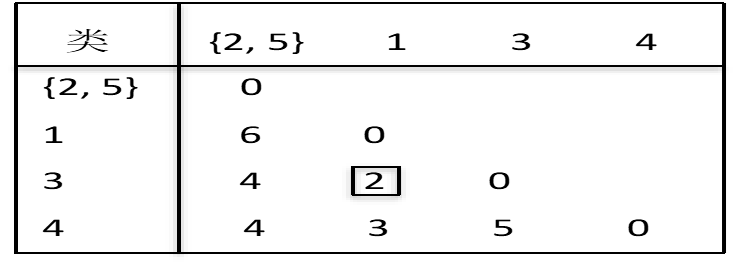
在这四个类中,最靠近的两个类是1和3,它们具有最小类间距离
min{6, 4, 4, 2, 3, 5}=d13=2
将1和3合并成一个新类{1,3}。第二次聚类后,各类之间距离如下表:
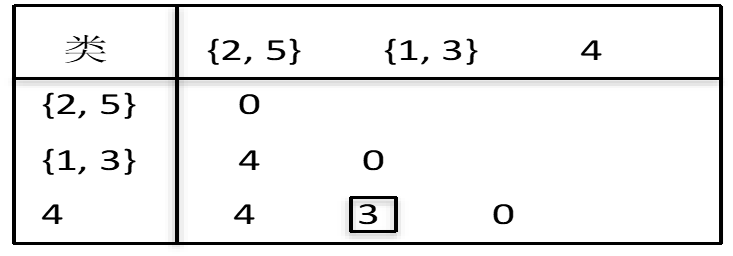
在这三个类中,最靠近的两个类{1,3}和4,它们具有最小类间距离:min{4, 4,3}=d{1,3}4=3
因此可将{1,3}和4再合并成一个新类{1,3,4}。第三次聚类后,各类之间距离如下表:
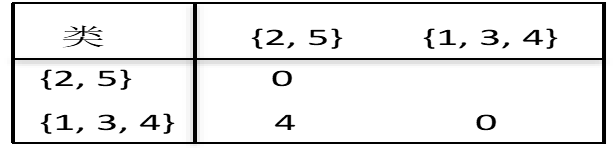
最后再将{2,5}和{1,3,4}合并成一个类,由此完成了整个聚类过程。相应的树形图如下图所示,从中可以清楚地看到整个聚类的过程。
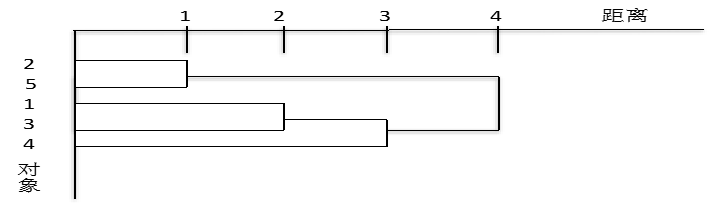
最长距离法
类间距离定义:两类中最远元素之间距离
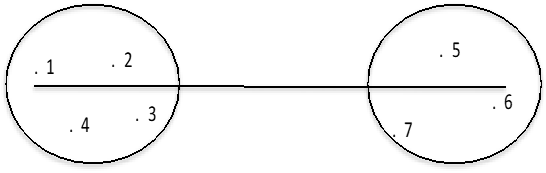
类间距离
1 | d{1, 2, 3, 4}{5, 6, 7} |
以类间距离为聚类依据,依次逐次选择类间最长距离进行聚类的过程叫最长距离聚类法。
依然使用上面的数据表格,使用最长距离法聚类的结果和树形图(Dendrogram)如下:
这里面非常重要的一点,在点合并的时候依然是选取最短距离,只是合并之后重新计算类间距离时,按照最长距离来计算
所以,同样地,一开始也是{2,5}被合并为同一类,第一次聚类后,各类之间距离如下表
| {2,5} | 1 | 3 | 4 | |
|---|---|---|---|---|
| {2,5} | 0 | |||
| 1 | 7 | 0 | ||
| 3 | 5 | 2 | 0 | |
| 4 | 5 | 3 | 5 | 0 |
这时{1,3}进行合并,第二次聚类后
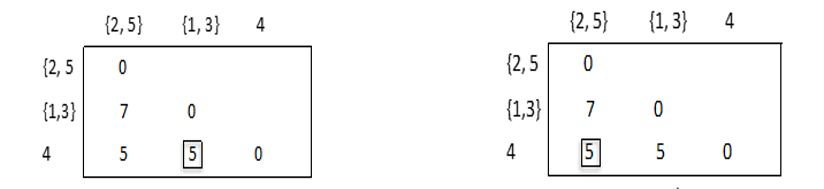
这时分两种情况
在这三个类中,最靠近的两个类{1,3}和4, {2,5}和4它们具有相同最小类间距离:
d{1,3}4=5 和d{2,5}4=5
因此可将{1,3}和4再合并成一个新类{1,3,4}; {2,5}和4再合并成一个新类{2,5,4}。第三次聚类后,各类之间距离如下表:

最后再将{2,5}和{1,3,4}、 {2,5,4}和{1,3}合并成一个类,由此完成了整个聚类过程。相应的树形图如下图所示,从中可以清楚地看到整个聚类的过程。
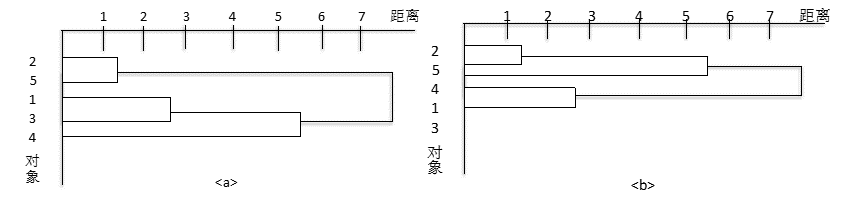
练习题
假定5个对象间的距离如下表所示,试用最短距离法聚类并画出树形图(Dendrogram)
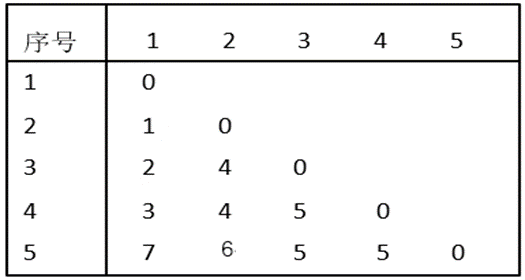
聚类过程为{1,2}-->{1,2,3}-->{1,2,3,4}-->{1,2,3,4,5}