遗传算法
基本概念
遗传算法(Genetic Algorithm,简称GA)
遗传算法的基本思想可归为三点:
1)遗传:子代总是和亲代相似。
2)变异:子代和亲代有某些不相似的现象。
3)选择:具有精选的能力,它决定生物进化的方向。
要点1:遗传算法按照一定的规则生成经过基因编码的初始群体,
要点2:然后从这些代表问题的可能潜在解的初始群体出发,挑选适应度强的个体进行交叉(或称交配、交换)和变异,以期发现适应度更佳的个体,
要点3:如此一代代地演化,得到一个最优个体,将其经过解码,该最佳个体编码则对应问题的最优解或近似最优解。
术语:
串:算法中的二进制串,对应于遗传学中的染色体。染色体是进化的信息载体。染色体可能发生突变,并因为这种突变,可能生成更好的、更能适应环境的后代。
基因:基因是串中的二进制位之数,基因用于表示个体的特征。基因是染色体遗传功能的最小操作单位。
基因位置:一个基因在串中的位置称为基因位置,有时也简称基因位或基因座。
基因特征值:在用串表示整数时,基因的特征值与二进制数的权一致。
种群:个体的集合称为种群,或称群体。生物的进化不是通过单个个体来实现的,而是一代代的种群同时进行。
种群大小:种群中个体的数量称为群体的大小。
适应度:适应度表示某一个体对于环境的适应程度。在GA中,也称做适值函数,用以估计个体的优劣。适应度值越高,被选来交配和进行后继遗传行为的概率也就越大。对于给定的优化问题,将其目标函数作为适应度函数。
遗传算法思路
1、将所有自变量进行编码。常用一组二进制码代表一个自变量的各种取值。
2、将各自变量取值的二进码连成一串,将得到一组二进制代码串。该串代表了自变量的一组取值所决定的解值域,最优解含于其中。
3、每一个可能的解(个体)构成种群
4、每个个体对应于优化问题的一个可行解,优化问题的目标函数作为种群所处的环境,而目标函数值则作为个体对环境的适应度。
5、优化由三种运算进行,运算包含三个基本算子:
选择(繁殖):选择算子从一个旧群体(父代)中选出合适的个体,产生新群体(后代)的过程。
交叉(重组):交叉算子选择两个不同个体的染色体(二进制串)的部分基因进行交换,形成新个体。该算子确定和扩充解空间,是一个随机化的重组算子。在很大程度上遗传算法的性能取决于所使用的交换算子的性能。
变异(突变):变异算子对某些个体的某些基因进行变异。在通常的二进制编码方式下,变异操作就是简单地将基因值取反(1变0、0变1)。
GA经过这三种运算可起到产生优良后代的作用。这些后代需满足适应值,经过若干代的遗传,将得到满足要求的后代(问题的解)。
基本遗传算法
遗传算法分为基本遗传算法和高级遗传算法,仅使用选择算子,交叉算子和变异算子的最基本的遗传算法称为基本遗传算法.
例题:计算f(x)=x^2 ,xɛ[0,31]的最大值
选择(或复制)算子
复制操作的初始种群(旧种群)的生成往往是随机产生的。例如我们可以通过投掷硬币20次,可产生维数n=4的初始种群如下(正面=“1”,背面=“0”):
0 1 1 0 1、1 1 0 0 0、0 1 0 0 0、1 0 0 1 1
上述通过抛掷一个均匀的硬币20次得到的初始种群,可以看作是一个长度为5位的无符号二进制数。将其编号成四个位串:
•位串1:0 1 1 0 1 (相当于十进制数:13)
•位串2:1 1 0 0 0 (相当于十进制数:24)
•位串3:0 1 0 0 0 (相当于十进制数:8)
•位串4:1 0 0 1 1 (相当于十进制数:19)
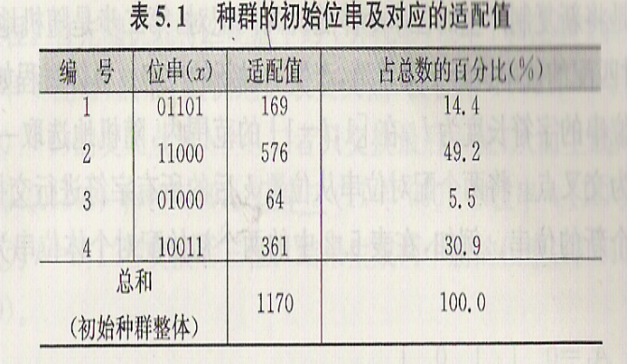
遗传算法每一代都是从选择(复制)开始。一种较为简单的选择方法是使用轮盘赌转盘上按比例划分的区域。每个区域代表一个个体。依表5.1可绘制出如图5.2所示的轮盘赌转盘。
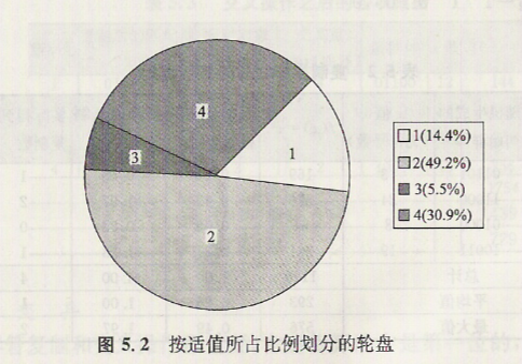
选择(复制)时,只是简单的转动这个按权重(适值占总和的百分比)划分的转盘4次,从而产生4个下一代的种群。例如对于表5.1中的位串1其适值为169,为总适值的14.4%,因此,每转动一次轮盘,指向位串的概率为0.144。这样位串的适值越高,在其下一代中产生的后代越多。当一个位串被选中时,此位串将被完整的复制,然后将复制位串送入匹配池中。
在本例中,位串1被复制一次,位串2被复制两次,位串3被淘汰,位串4被复制一次。
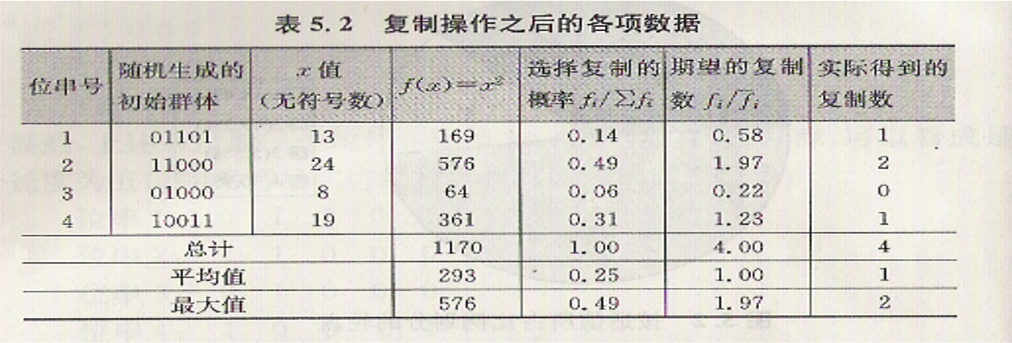
交叉算子
简单的交叉操作分两步实现。在由等待配对的位串构成的匹配池中,第一步是将新复制产生的位串个体随机两两配对,第二步是随机地选择交叉点,对匹配的位串进行交叉繁殖,产生一对新位串。
交叉方法:设位串的字符长度为L,在[1,L-1]的范围内,随机地选取一个整数值K作为交叉点。将两个配对位串后的所有字符进行交换,从而生成两个新的位串。

表5.3列出了交叉操作过程。首先随机将匹配池中的个体配对,然后,随机地选取交叉点,设位串1(0110|1)和位串2(1100|0)的交叉点为k=4,二者只交换最后一位,从而生成两个新的位串,即(01100)和(11001)。位串3(11|000)和位串4(10|011)的交叉点为k=2,二者交换后三位。结果生成两个新的位串,即(11011)和(10000)。
变异算子
仅有交叉操作存在的问题:尽管复制和交叉操作很重要,在遗传算法中是第一位的,但不能保证不会遗漏一些重要的遗传信息。
例如:表5.4中无论怎样交叉,在位置4上都不可得到有1的位串。若优化的结果该位串上要求该位置是1,显然仅靠交叉是不够的,还需要有变异,即特定位置上的0和1之间的转变。
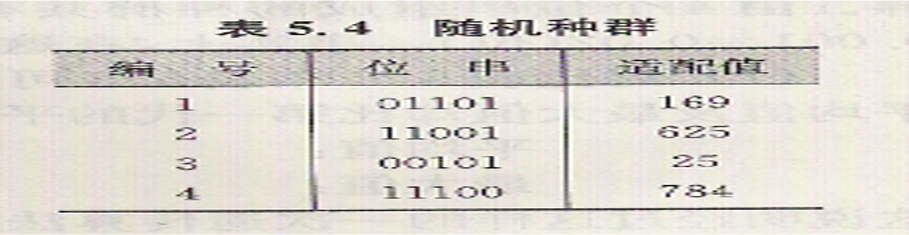
变异方法:
在简单遗传算法中,变异就是某个字符串某一位的值偶然的(概率很小的)随机的改变,即在某些特定位置上把1变成0,或反之。变异是沿着位串字符空间的随机移动。根据经验的研究,为了取得好的结果,变异的频率为每一个千位的传送中,只变异一位,即变异的概率为0.001。
例:在表5.4所示的种群中共有20个串字符号(每个位串的长度为5个字符位)。期望的变异串位数为20*0.001=0.02(位),所以在此例情况下无串位值的改变。
注:变异在遗传算法中的作用是第二位的,但却是必不可少的。变异操作可以起到恢复位串字符多样性的作用,并能适当地提高遗传算法的搜索效率。
上面流程的完整步骤为:
