LSTM和GRU

发表于 | 分类于

LSTM和GRU

RNN的优缺点

优点：

  1. 可以捕获序列之间的关系；
  2. 共享参数。

缺点：

  1. 存在梯度消失和梯度爆炸问题；
  2. RNN的训练是一个比较困难的任务；
  3. 无法处理长序列问题。

LSTM

LSTM可以处理长序列问题，同样在之前这篇文章中，关于LSTM网络的核心思想介绍的比较明白，而且传送带的比喻比较形象，结合上篇和当前这篇可以对LSTM有更深入的理解。

接着上篇文章中的例子，RNN一个时间步t的输出为(实际上这里只是相当于计算t+1的State，并非真正的输出，输出output = activation(dot(State_t+1, V)+b))：

1
y = activation(dot(state_t, U) + dot(input_t, W) + b)

LSTM多了一个Ct（这里描述的LSTM的输出也并不完全准确，只是帮助理解，具体还需要看下面的结构图）：

1
output_t = activation(dot(state_t, Uo) + dot(input_t, Wo) + dot(C_t, Vo) + bo)

Ct的计算方式：

1
2
3
4
5
i_t = activation(dot(state_t, Ui) + dot(input_t, Wi) + bi)
f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bf)
k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bk)

c_t+1 = i_t * k_t + c_t * f_t

接下来先看看LSTM的网络结构图，可以帮助更好的理解上面的计算含义

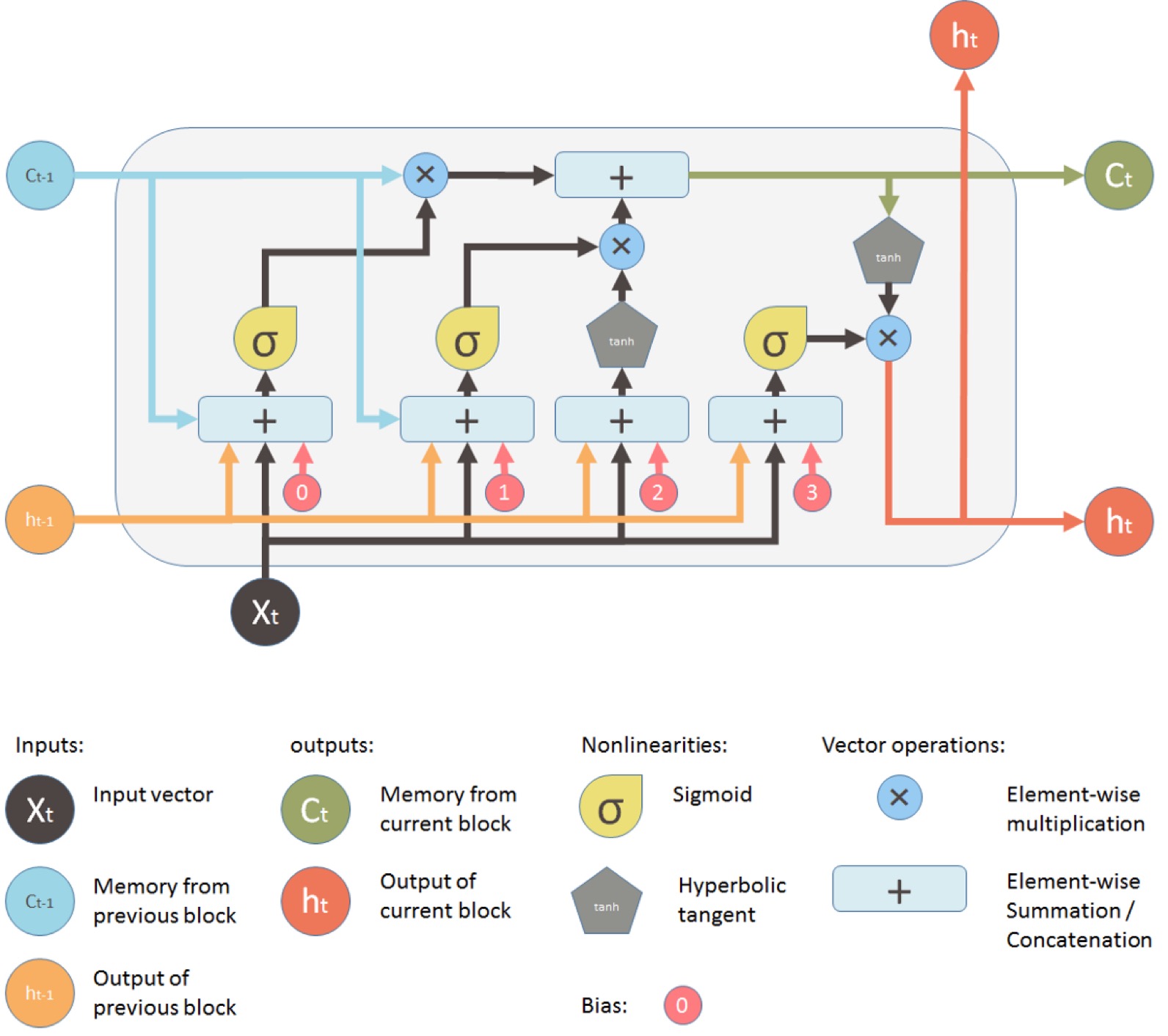
c_t+1 = i_t * k_t + c_t * f_t，其中f_t是下面这部分（也就是forget gate）

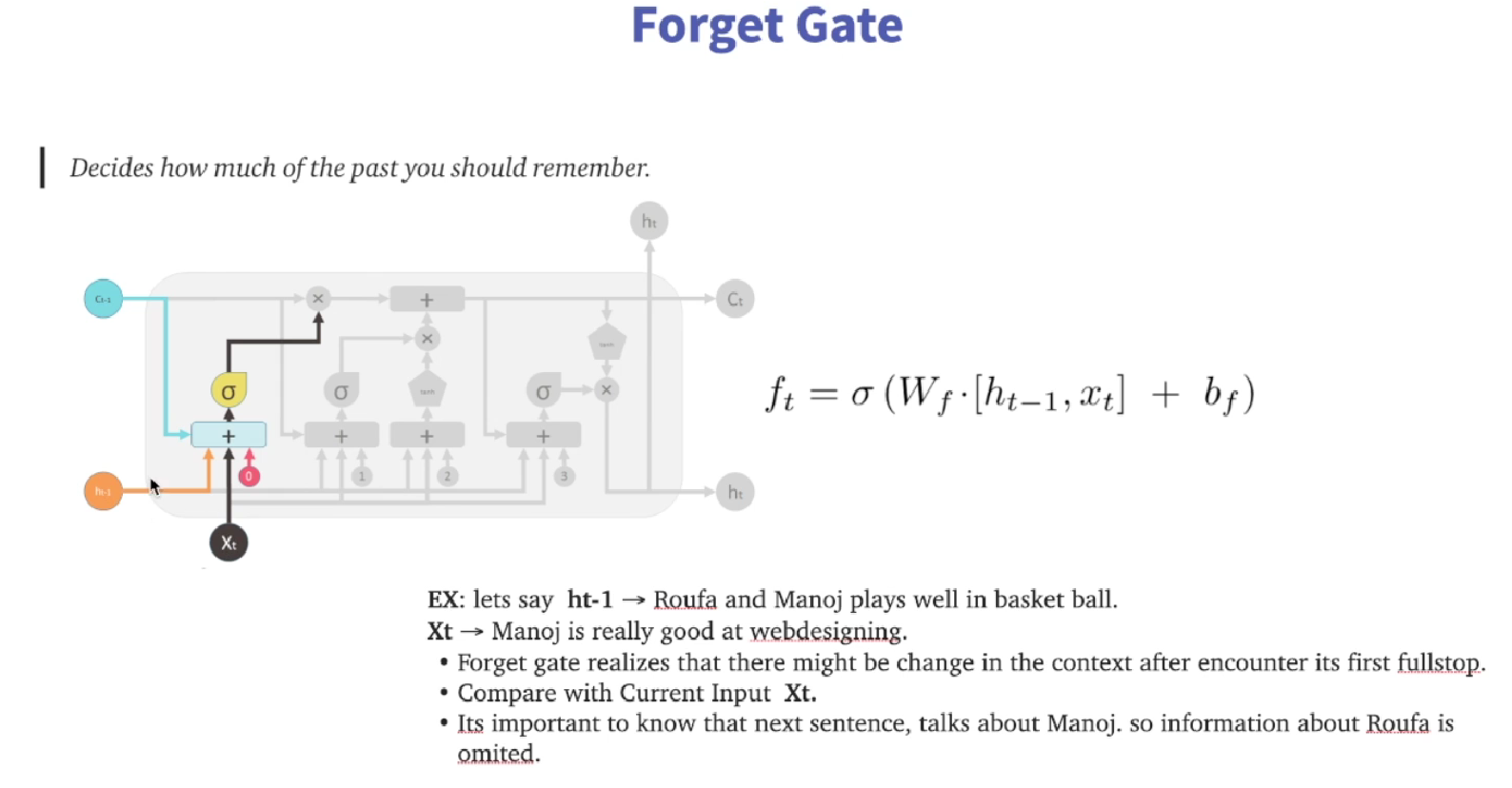
遗忘门决定需要遗忘多少之前的状态，这是通过当前的输入和上一个时间步的隐藏状态计算得到的。将这两者通过一个全连接层并应用 sigmoid 函数，得到遗忘门的值。这个值在 0 到 1 之间，0 表示完全遗忘，1 表示完全保留。

遗忘门的计算公式如上图中所示，其中Wf是权重矩阵，bf是偏置项，ht-1是上一时刻的隐藏状态，xt是当前输入，σ是sigmoid函数。

i_t*k_t是下面这部分（也就是update gate,网上一般将此门称为输入门）

LSTM需要决定哪些新的信息需要存储到记忆细胞中。这包括两部分：一部分是输入门，它决定将更新记忆细胞的哪些部分；另一部分是一个tanh层，它创建了一个新的候选值向量，这个向量可能会被添加到记忆细胞中，输入门的值和候选值都是通过当前的输入和上一个时间步的隐藏状态计算得到的。 输入门的计算公式如上图中的t，候选值的计算公式如上图中的’t

根据遗忘门和输入门的值来决定更新记忆细胞。将细胞状态(Ct-1，即上一时间步得到的C)与遗忘门的值相乘，表示遗忘了一部分的状态信息；然后将输入门的值与候选值相乘并加上去，表示添加了一部分新的状态信息。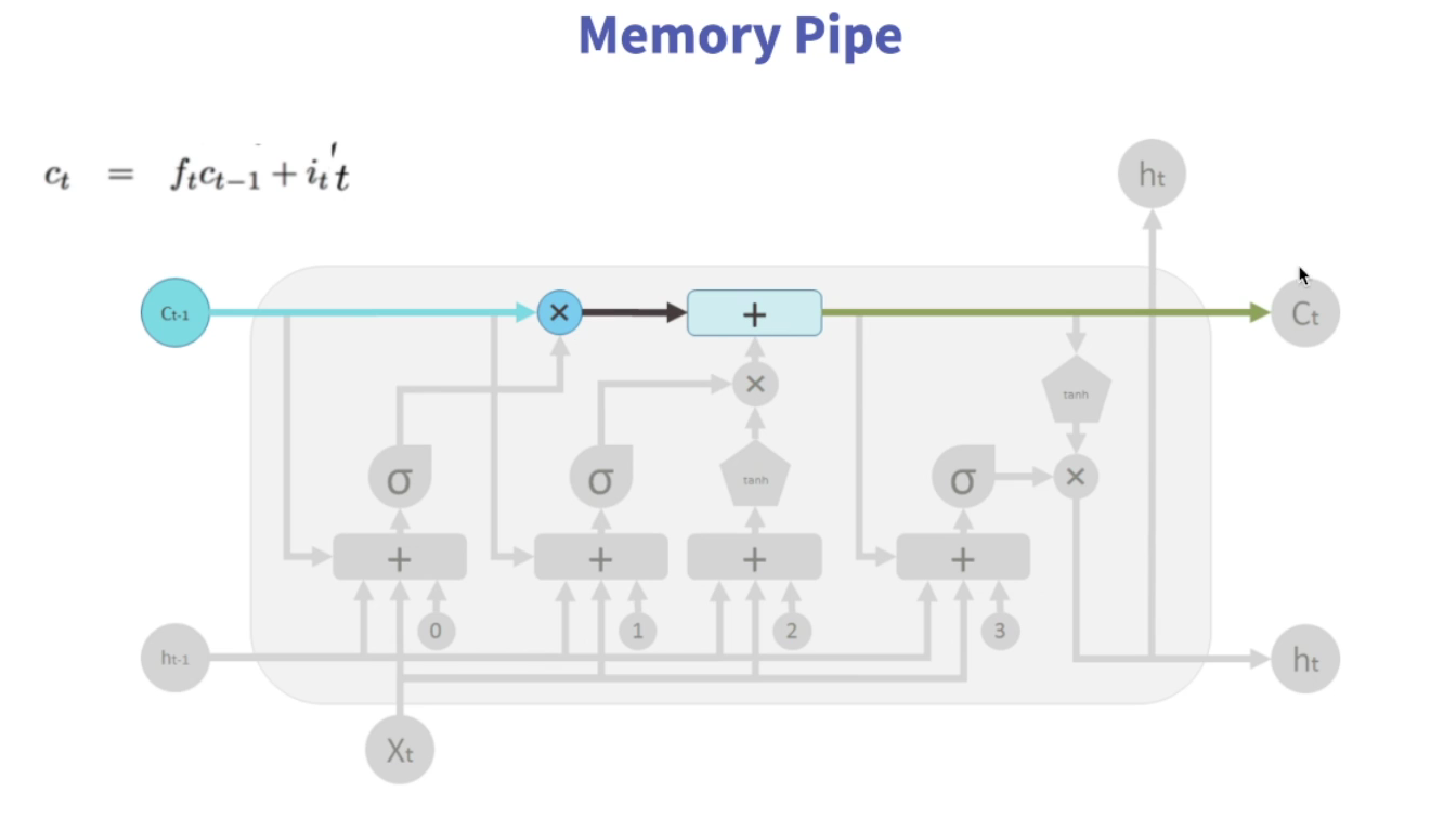

别忘了，以上只是在计算Ct，Ct只是LSTM相比较于RNN增加的部分，真正的输出(ht，这个ht或许也不能称作输出？只是隐藏状态？)是下面这部分

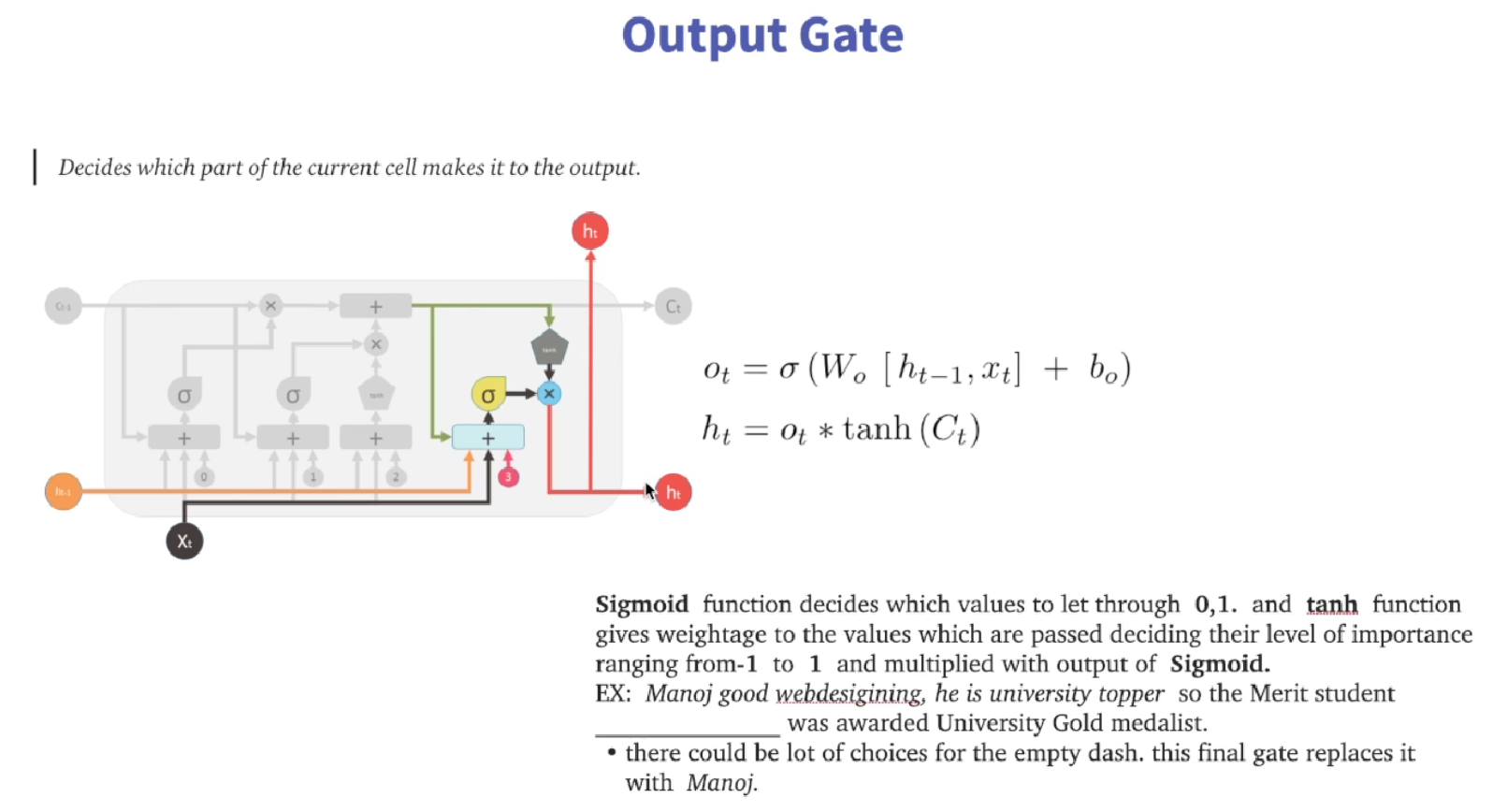
输出门：决定将基于细胞状态输出什么。通过当前的输入和上一个时间步的隐藏状态通过一个全连接层并应用sigmoid函数，得到输出门的值,这个值在0到1之间，0表示完全不输出，1表示完全输出。 然后将细胞状态通过tanh函数得到一个值在 -1 到 1 之间的结果，并与输出门的值相乘，得到最终的隐藏状态。

可以看到所谓的遗忘门、输入门、输出门的公式是完全一样的，只不过使用了三个不同的全连接层，即三个权重矩阵W和三个不同的偏执。

总结：遗忘门·上一个细胞状态表示遗忘多少，输入门·候选值表示本次更新多少，这两个加一起形成这一时间步的细胞状态Ct，输出门·tanh(Ct)得到最终隐藏状态。

代码实现

仅返回最终输出

1
2
3
4
5
6
7
# 32个句子，每个句子长度为10，词向量长度为8
inputs = tf.random.normal([32, 10, 8])
lstm = tf.keras.layers.LSTM(4)
output = lstm(inputs)
print(output.shape)

(32, 4)

返回每个时间步的输出

1
2
3
4
# 这里每个句子的长度为10，正常一个句子会有一个向量输出，如果return_sequences=True，则句子中每个单词均会有一个输出。
lstm = tf.keras.layers.LSTM(4, return_sequences=True)
out = lstm(inputs)
print(out.shape)

返回除最后一个输出之外的最后一个状态

1
2
3
4
5
6
7
8
9
10
11
lstm = tf.keras.layers.LSTM(4, return_sequences=False, return_state=True)
# 会同时返回h状态和c状态，不过仅是最后一个状态
# return_sequences=False时，h状态和out的值是一样的
out, h_state, c_state = lstm(inputs)
print(out.shape)
print(h_state.shape)
print(c_state.shape)

(32, 4)
(32, 4)
(32, 4)

返回所有时间步的输出和最后一个状态

1
2
3
4
5
6
7
8
9
10
lstm = tf.keras.layers.LSTM(4, return_sequences=True, return_state=True)
# out = lstm(inputs)
out, h_state, c_state = lstm(inputs)
print(out.shape)
print(h_state.shape)
print(c_state.shape)

(32, 10, 4)
(32, 4)
(32, 4)

GRU

LSTM参数过多，计算量大，也存在梯度消失的问题，为解决计算量过大的问题，将LSTM中的遗忘门和输入门简化为一个更新门，这就是GRU。

单个GRU的结构图：

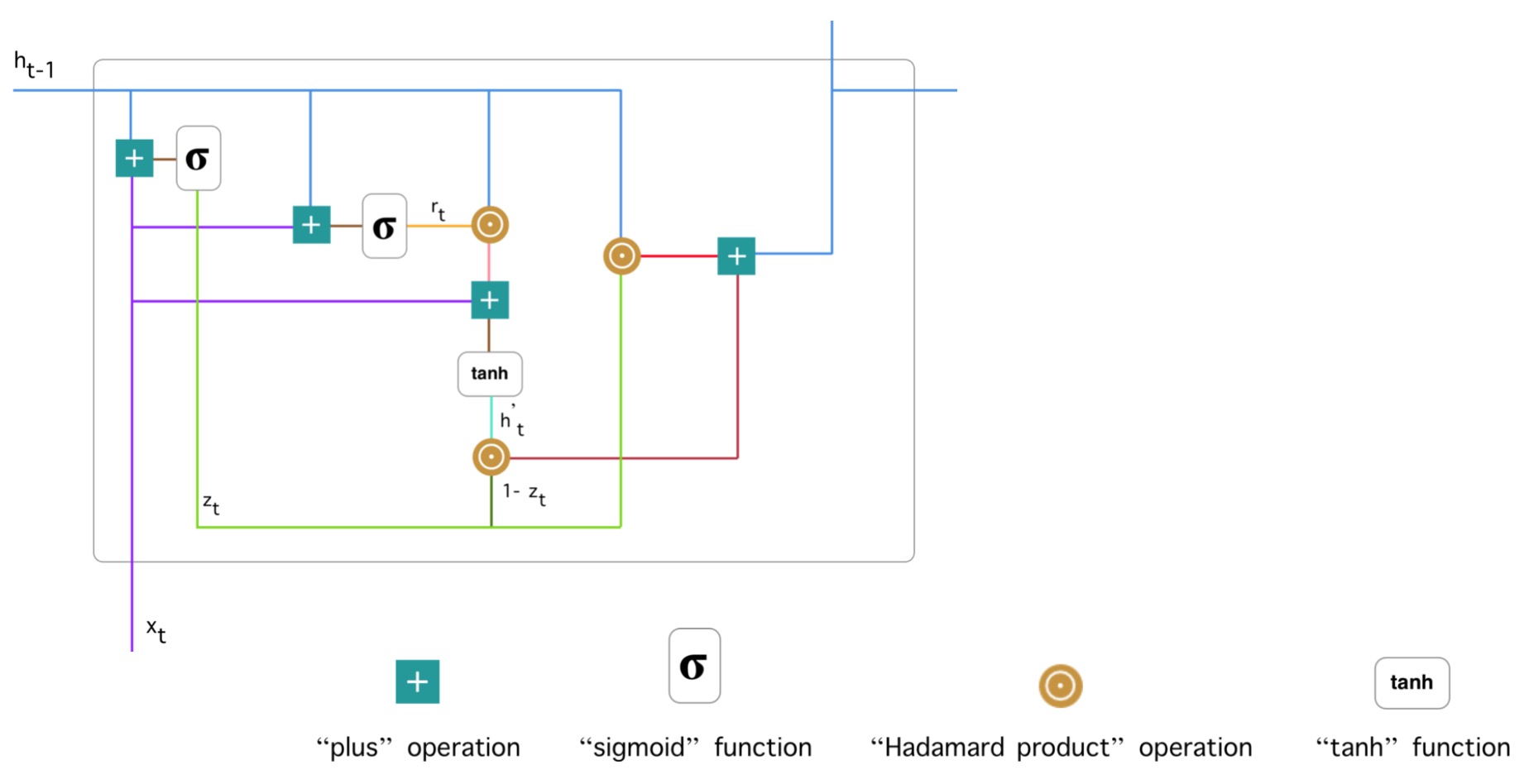
下面是整个图的拆解图

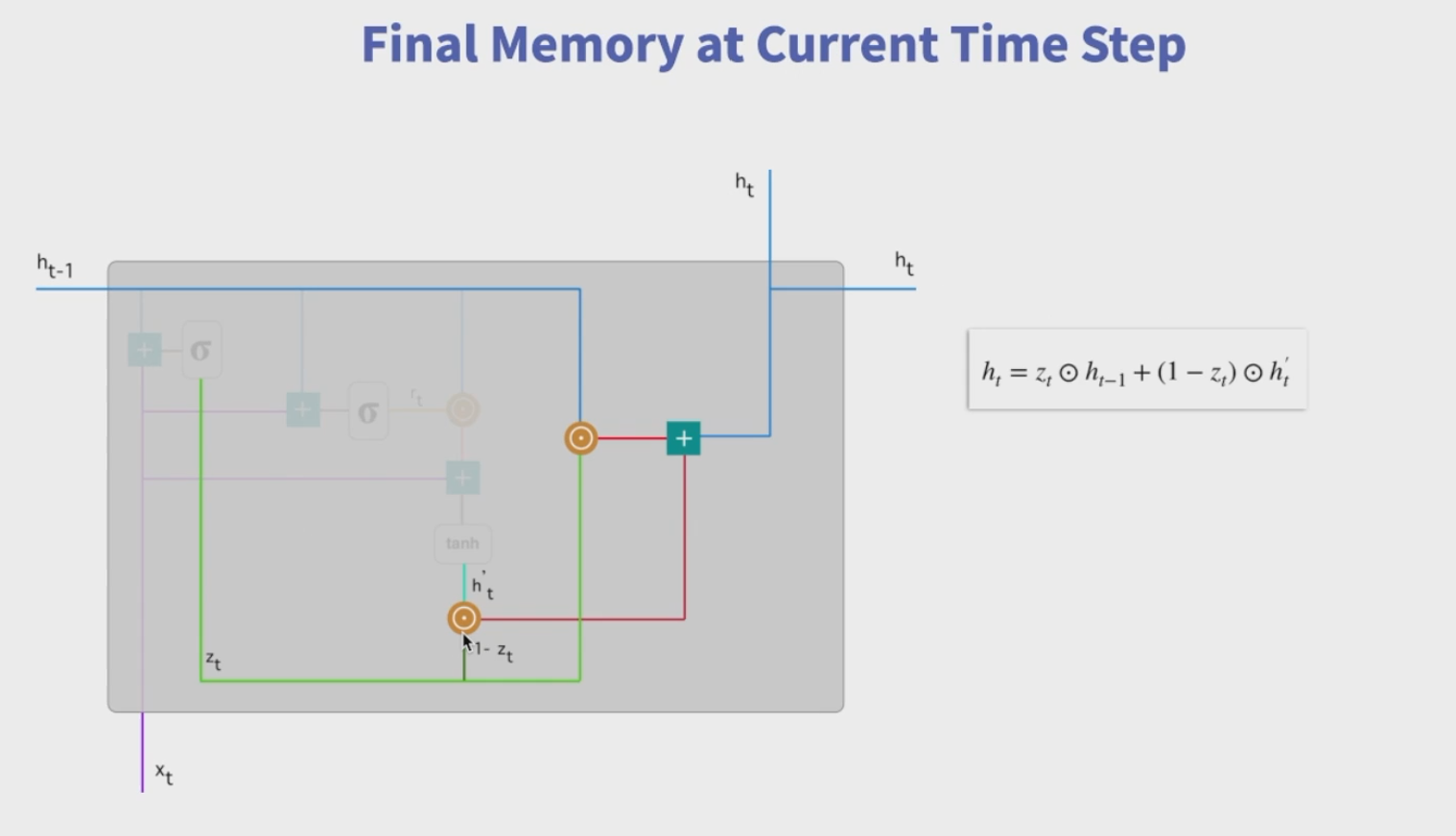
代码实现

1
2
3
4
5
6
inputs = tf.random.normal([32, 10, 8])
gru = tf.keras.layers.GRU(4)
output = gru(inputs)
print(output.shape)

(32, 4)
1
2
3
4
5
6
7
8
# return_sequences参数的用法和lstm一样
gru = tf.keras.layers.GRU(4, return_sequences=True, return_state=True)
out, final_state = gru(inputs)
print(out.shape)
print(final_state.shape)

(32, 10, 4)
(32, 4)

注意，这里GRU返回值只有两个，相比LSTM，没有c_state，这个也正是GRU相比于LSTM的优化点，后面会进一步说明。同样的，当return_sequences=False时，out和final_state的值是一致的。

LSTM VS GRU

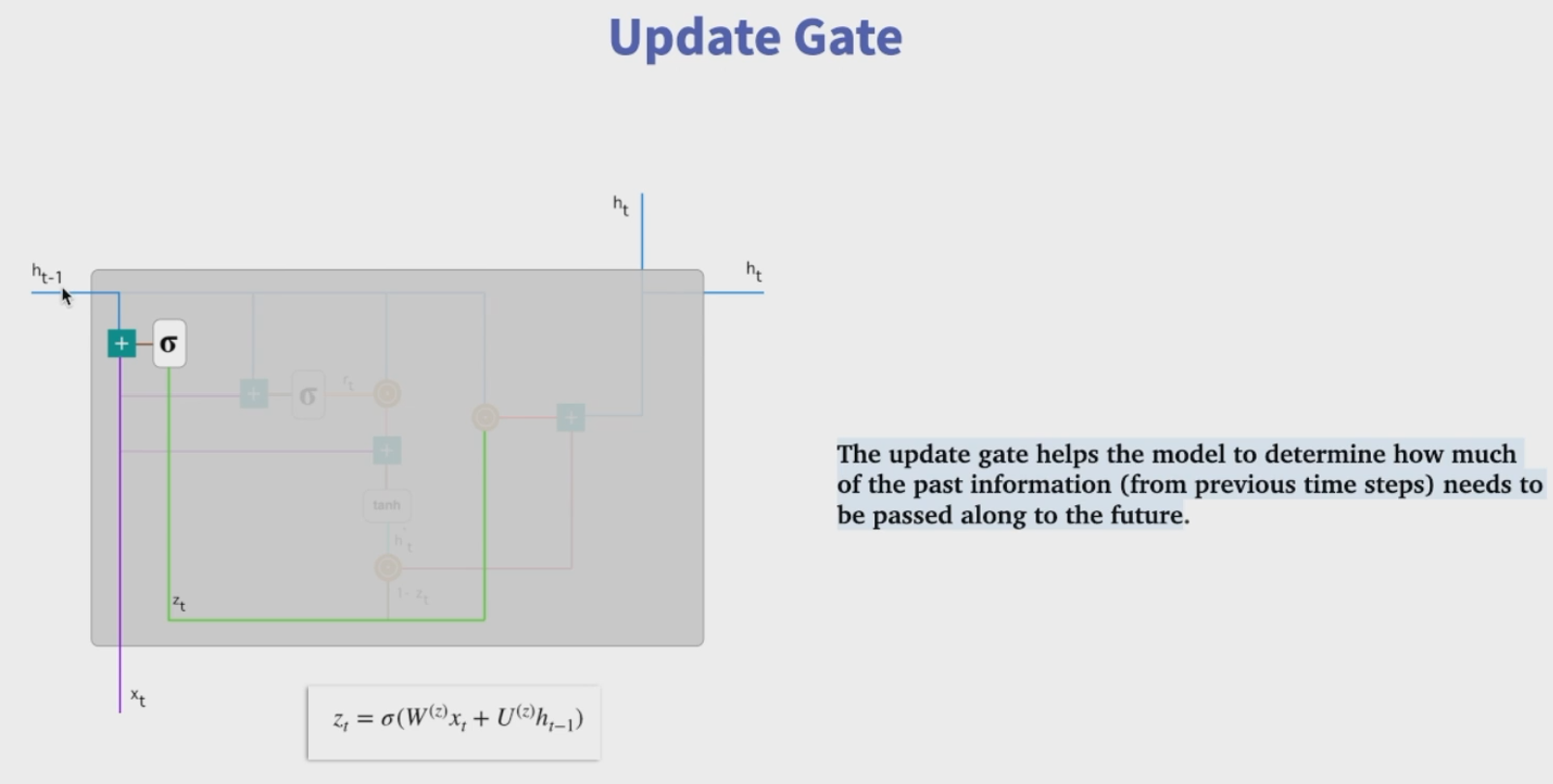
  1. GRU 只有两个门。GRU 将 LSTM 中的输入门和遗忘门合二为一，称为更新门（update gate），控制前边记忆信息能够继续保留到当前时刻的数据量，或者说决定有多少前一时间步的信息和当前时间步的信息要被继续传递到未来；GRU 的另一个门称为重置门（reset gate），控制要遗忘多少过去的信息。

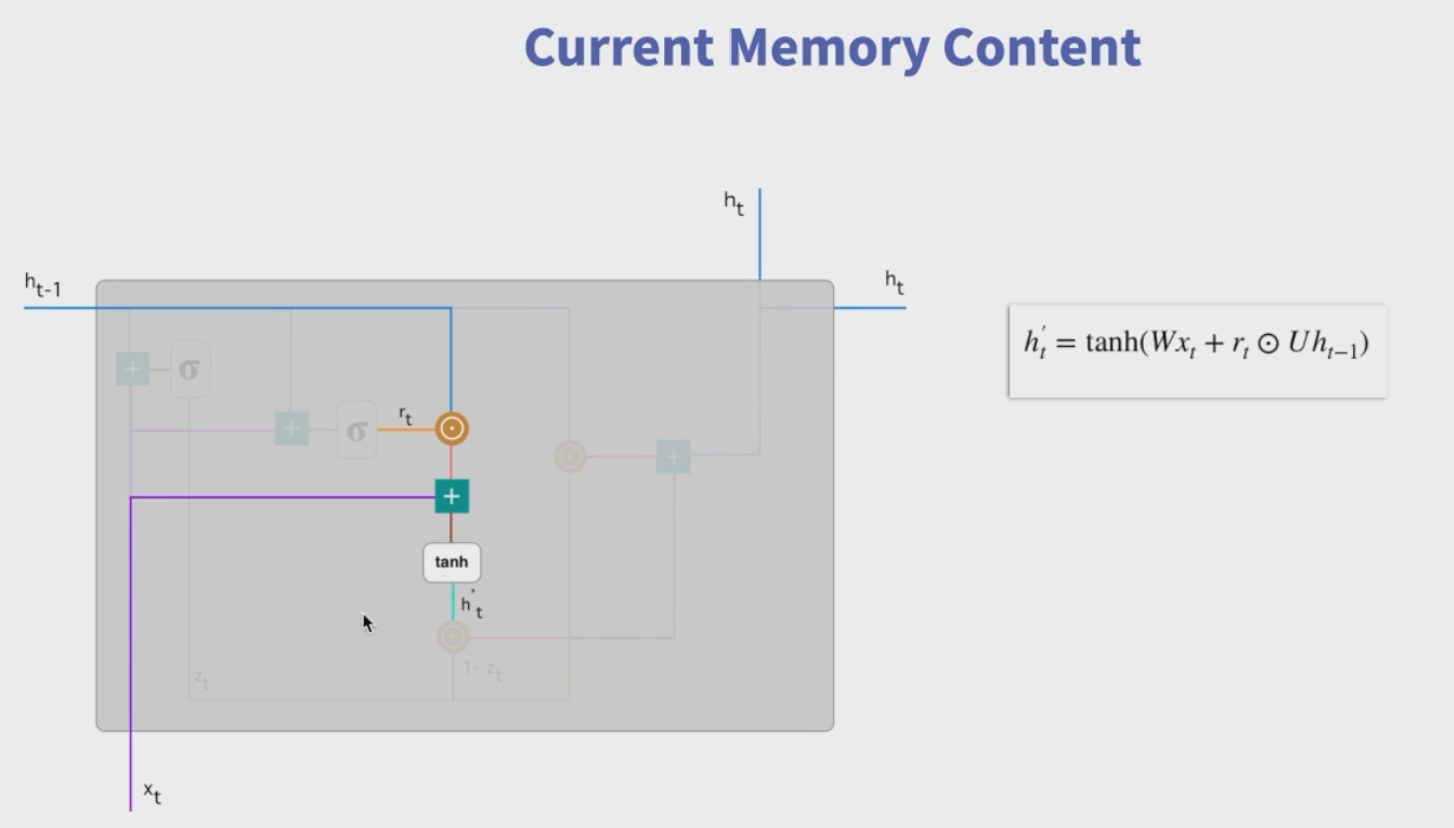
  2. 取消进行线性自更新的记忆单元（memory cell，也就是不再使用c_state），而是直接在隐藏单元中利用门控直接进行线性自更新。

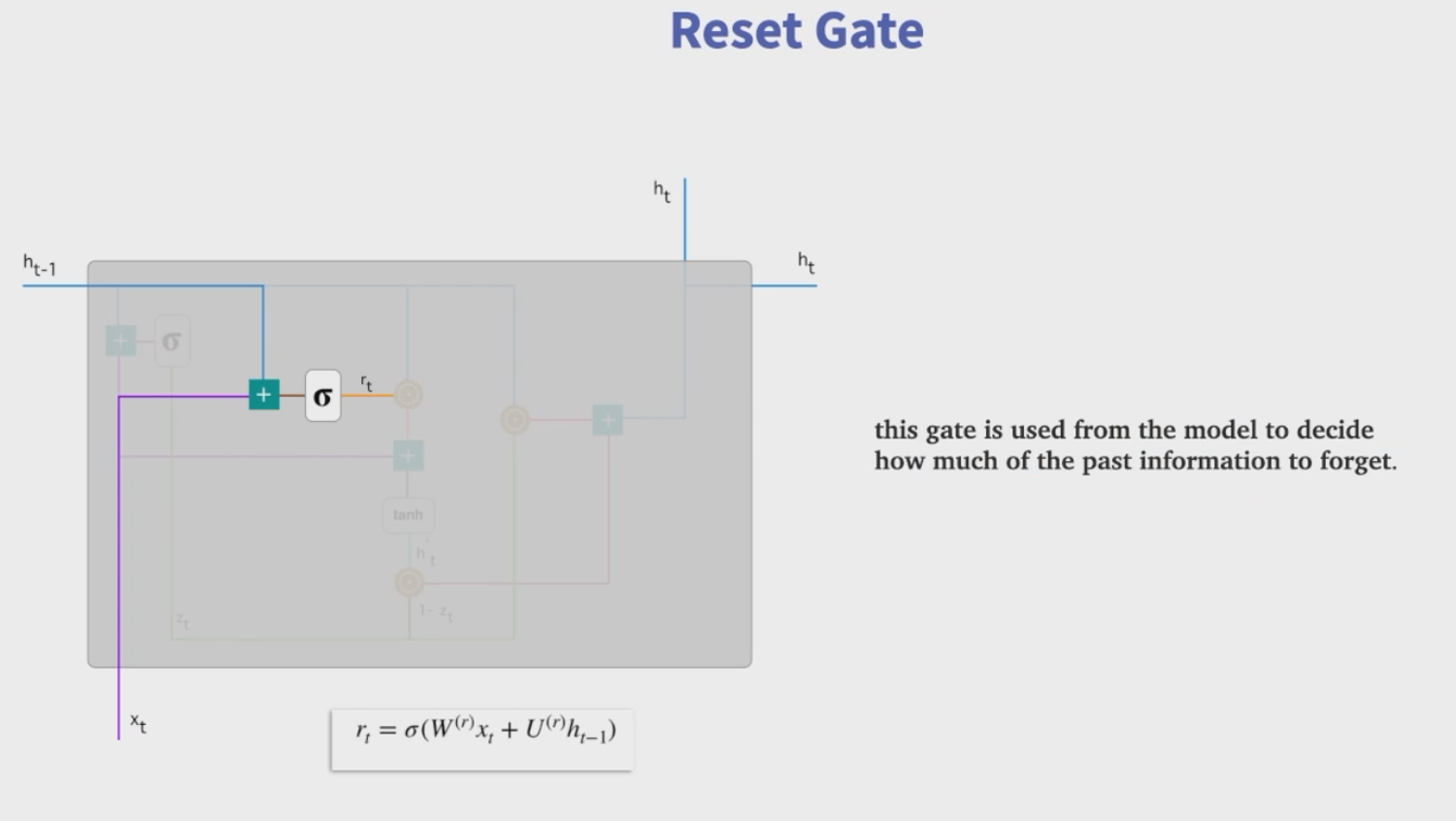
  3. 利用重置门重置记忆信息，GRU 不再使用单独的记忆细胞存储记忆信息，而是直接利用隐藏单元记录历史状态。利用重置门控制当前信息和记忆信息的数据量，并生成新的记忆信息继续向前传递。

  4. 利用更新门计算当前时刻隐藏状态的输出，隐藏状态的输出信息由前一时刻的隐藏状态信息h_(t-1)和当前时刻的隐藏状态输出h_t ，利用更新门控制这两个信息传递到未来的数据量。