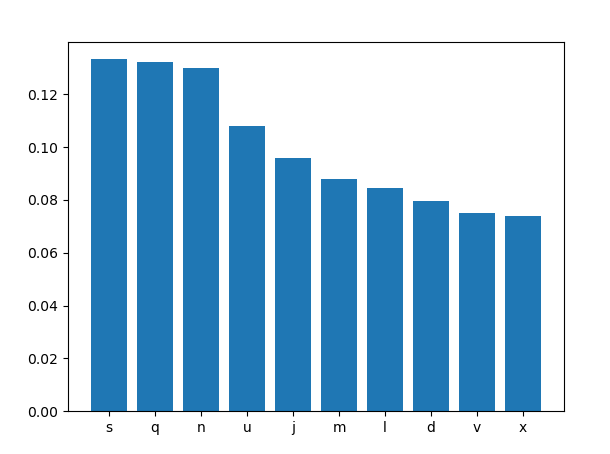
NLG 采样策略

`NLG` 采样策略

上篇文章中学习了NLG的解码策略，主要包括greedy search、beam search，如果不太记得了可以再去温习一下，然后接下来我们来看看这些解码策略会存在哪些问题，是否还可以从其他角度来提高文本的生成效果。

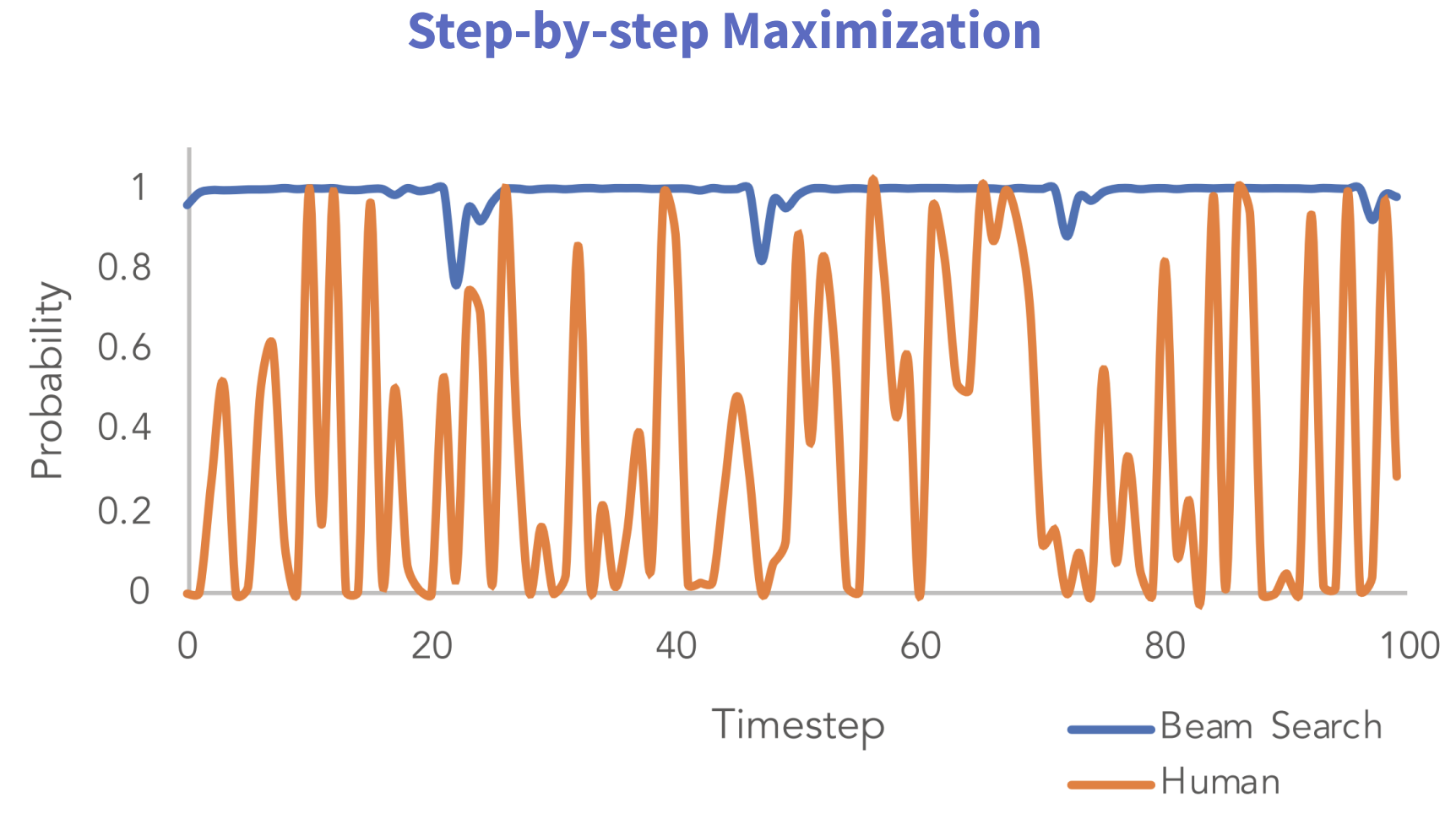
这幅图展示了每个时间步，生成某个单词的可能性，我们发现beam search在每一步的概率值都是比较大的，但是如果是真实人类的话，其实是比较随机的（人说话的内容比较随机，富有多样性）。这主要是因为beam search本身就是在根据最大概率去生成句子，但是最大概率不等于最好，上篇文章中我们有提到

当k比较小时，生成的句子可能会不符合语法规则，不自然，无意义，不正确（比较死板）；
当k比较大时，计算量会增大，虽然生成的句子更通顺，但是也存在偏离主题的可能性。

此外因为模型生成时，一定程度上依赖于已经生成的句子，所以一味的选取概率最大的，可能会使句子的生成陷入不断地重复循环中，所以针对beam search这些特点，为了可以生成更多样化的句子(引入一定的随机性)又不偏离主题，以下几种采样策略被研究者提出。

Temperature Scaling

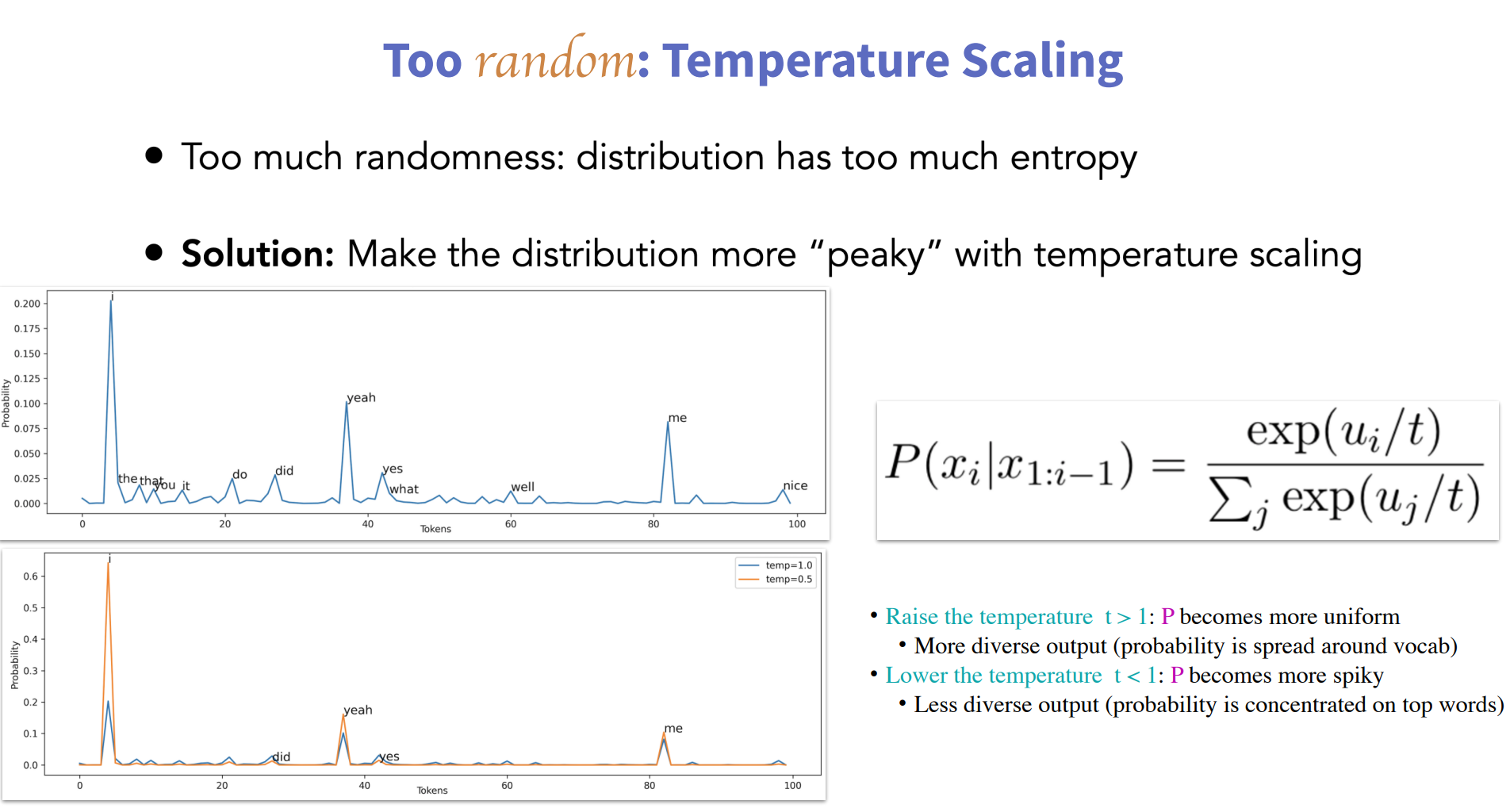
为了引入随机性，最直接有效的方式就是基于概率分布随机选取单词，但这样带来的问题是，如果我们有5万种可能的选择，即使最低的25000个token每个都不太可能，但是他们的概率加起来可能有30%。这意味着，对于每个样本，我们都有三分之一的概率完全偏离训练的结果。由于前面提到的上下文一般较短，每个待生成的token比较依赖历史最近生成的文本，这样会导致误差不但传递放大。

为了缓解上述问题，temperature scaling的方法被提出，其主要思想对原始的概率分布进一步放缩，使概率较大的更大，概率较小的更小，这样可以减少随机到概率比较小的单词的可能性，使模型尽可能在概率较大的几个单词之间随机，通过在softmax中增加超参t来实现。

top-k sampling

学习temperature scaling的主要思想之后，其实很容易理解top-k sampling的原理，temperature scaling通过概率缩放之后，使得概率较大的词被选取的几率变大，而top-k 则直接限定了仅在概率最高的k个单词之间按照概率采样，k是超参数。k如果等于1，那么此方法就与greedy search等价。

top-k在具体实现时还有一点就是，选取概率最大的前k个词之后，会把其他词的概率全部置0，然后对这k个词的概率进行重新计算，使这k个词之间的概率之差进一步缩小，从而引入随机性。不过top-k sampling算法也是有缺点的。

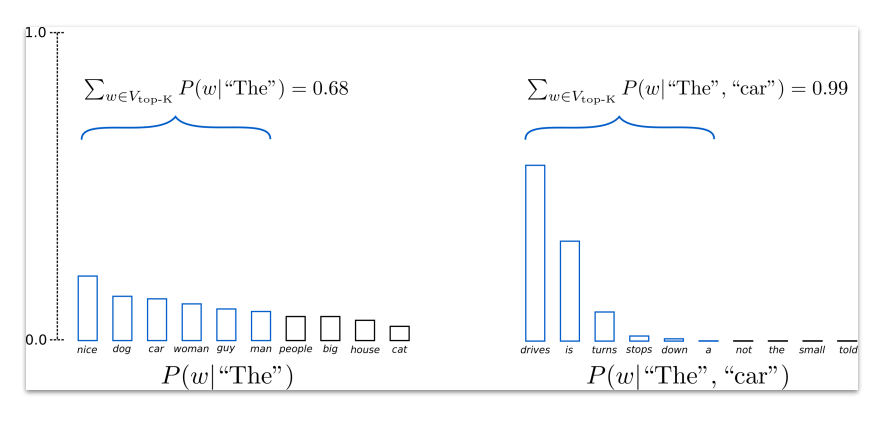
当词的概率分布比较平滑时（左图），选取前k大时，会丢弃掉与前k大的概率相差不多的词（本来也应该给他们一定的机会）；当词的概率分布比较陡峭时（右图），选取前k大时，可能会把概率极小的词也选进来，从而导致最终结果受到影响。为了解决top-k的问题，top-p sampling的算法被提出。

top-p sampling（Nucleus Sampling）

在每个时间步，解码词的概率分布可能存在80/20原则的情况（或者说长尾分布），即头部的几个词的出现概率已经占据了绝大部分概率空间，把这部分核心词叫做nucleus。

具体方法为：给定一个概率阈值p，从解码词候选集中选择一个最小集Vp，使得它们出现的概率和大于等于p。然后再对Vp做一次re-scaling，本时间步仅从Vp集合中解码。

其实top-k和top-p的本质是一样的，只区别在于置信区间的选择。有些时候top-k和top-p可以联合使用。

代码实现

这里我们还是使用上篇中的代码来模拟模型生成的概率

import numpy as np
import matplotlib.pyplot as plt


# 定义词典(就是26个英文字母)
dictionary = []
for c in range(ord('a'), ord('z')+1):
    dictionary.append(chr(c))

print(f'词典：{dictionary}')

# 模拟一个已经被训练好的LM


class LanguageModel:
    def __init__(self, dictionary):
        self.dictionary = dictionary

    def predict(self):
        output = np.random.rand(len(dictionary))
        output = output/output.sum()
        return output


model = LanguageModel(dictionary)

temperature scaling

def softmax(z):
    return np.exp(z)/sum(np.exp(z))


def temperature_sampling(conditional_probability, temperature=1.0):
    conditional_probability = np.asarray(conditional_probability).astype("float64")
    fig = plt.figure(figsize=(20, 10), dpi=80)
    ax1 = fig.add_subplot(2, 1, 1)
    ax1.bar(dictionary, conditional_probability)
    # plt.bar(dictionary, conditional_probability)
    # plt.show()
    # 注意这里，先对概率取对数，然后再除以t
    conditional_probability = np.log(conditional_probability) / temperature
    reweighted_conditional_probability = softmax(conditional_probability)
    # 此方法根据概率分布来随机，概率高的被随机到的可能性大，但是并不一定
    probas = np.random.multinomial(1, reweighted_conditional_probability, 1)
    # plt.bar(dictionary, reweighted_conditional_probability)
    # plt.show()
    ax2 = fig.add_subplot(2, 1, 2)
    ax2.bar(dictionary, reweighted_conditional_probability)
    plt.show()

    return np.argmax(probas)


predictions = model.predict()
for temp in np.arange(0.2, 1.6, 0.2):
    next_token = temperature_sampling(predictions, temperature=temp)
    print("Temperature: ", temp)
    print("Sampled token: ", dictionary[next_token], "\n")

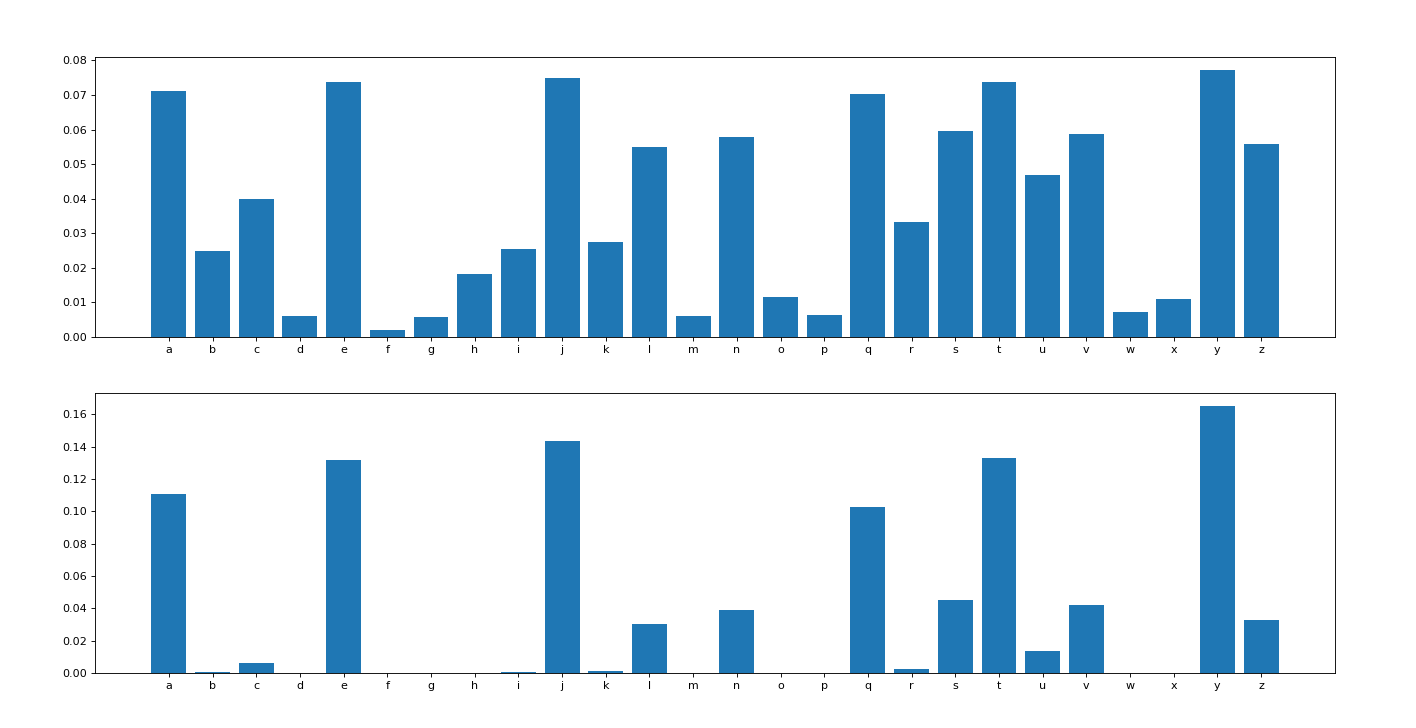
这里每隔0.2进行一次输出对比，感兴趣的可以观察随着t的变化，概率的二次分布变化情况，我这里放出t=0.2和t=1.4时的对比情况（t=1时，相当于无变化）

t=0.2时：

t = 1.4时：

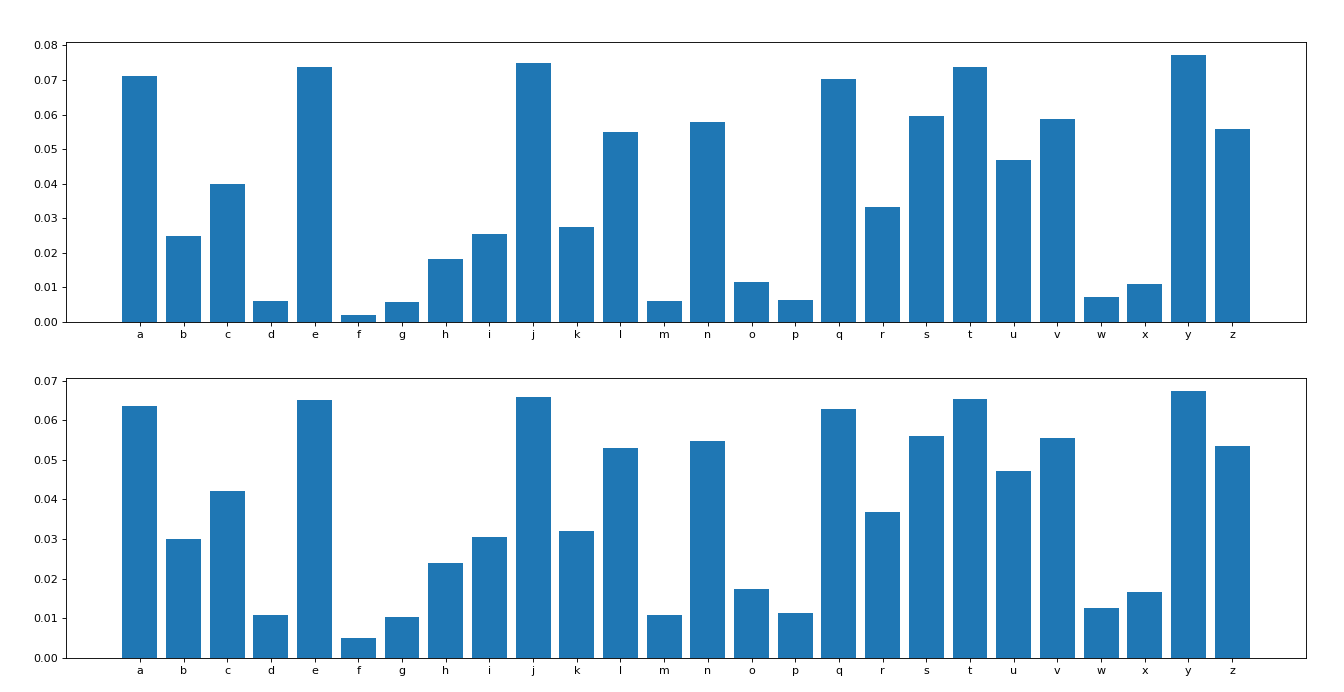
观察后的结论：temperature的选择，往往呈现如下规律：

当 temperature 设置为较小或者0的值时（会使概率小的几乎变为0）， Temperature Sampling 等同于每次选择最大概率的 Greedy Search。
小的temperature 会引发极大的 repetitive 和predictable文本，但是文本内容往往更贴合语料(highly realistic)，基本所有的词都来自与语料库。
当temperatures较大时（可以一定程度把概率小的词概率变大）, 生成的文本更具有随机性( random)、趣味性( interesting)，甚至创造性( creative); 甚至有些时候能发现一些新词(misspelled words) 。
当设置高 temperature时（所有词的概率会相差不大），文本局部结构往往会被破坏，大多数词可能会是semi-random strings 的形式。
实际应用中，往往experiment with multiple temperature values! 当保持了一定的随机性又能不破坏结构时，往往会得到有意思的生成文本。

top-k sampling

def top_k_sampling(conditional_probability, k):
    # 先抽取前k个概率最大的
    top_k_probabilities, top_k_indices = tf.math.top_k(conditional_probability, k=k, sorted=True)
    top_k_indices = np.asarray(top_k_indices).astype("int32")
    # 将抽取到的k个概率值，re-scaling
    top_k_redistributed_probability = softmax(np.log(top_k_probabilities))
    top_k_redistributed_probability = np.asarray(top_k_redistributed_probability).astype("float32")
    # 根据概率分布进行选择，概率大的可能会选择的可能性大，但并不一定
    sampled_index = np.random.choice(top_k_indices, p=top_k_redistributed_probability)
    top_k_tokens = [dictionary[i] for i in top_k_indices]
    plt.bar(top_k_tokens, top_k_redistributed_probability)
    plt.show()
    return sampled_index

# top-k sampling 测试
next_token = top_k_sampling(predictions, k=5)
print(f"top-k sampling result: {dictionary[next_token]}")

top-k sampling result: i

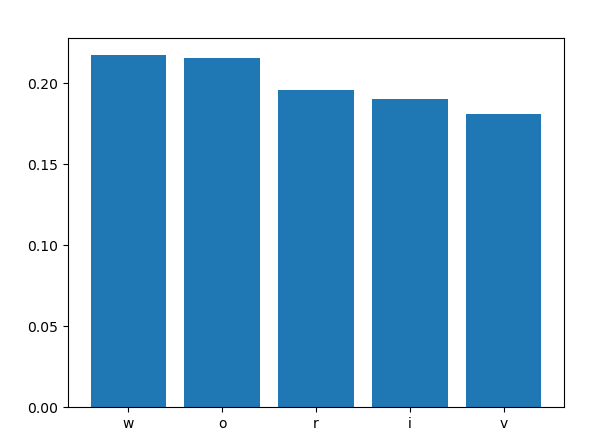
这里概率最大的五个字符分别为w、o、r、i、v，并且其中i的概率并非最大，但是依然被本次随机到了。

top-p sampling

def top_p_sampling(conditional_probability, p):
    # 对conditional_probability排序，返回排序后的索引
    sorted_index = tf.argsort(conditional_probability, direction="DESCENDING")
    print(sorted_index)
    sum_p = 0.0
    selected_index = []
    top_p_probabilities = []
    for index in sorted_index:
        sum_p += conditional_probability[index]
        selected_index.append(index)
        top_p_probabilities.append(conditional_probability[index])
        if sum_p >= p:
            break

    # 将抽取到的概率值，re-scaling
    top_p_redistributed_probability = softmax(np.log(top_p_probabilities))
    top_p_redistributed_probability = np.asarray(top_p_redistributed_probability).astype("float32")
    # 根据概率分布进行选择，概率大的可能会选择的可能性大，但并不一定
    sampled_index = np.random.choice(selected_index, p=top_p_redistributed_probability)
    top_p_tokens = [dictionary[i] for i in selected_index]
    plt.bar(top_p_tokens, top_p_redistributed_probability)
    plt.show()
    return sampled_index

prediction = model.predict()
next_token = top_p_sampling(predictions, 0.6)
print(f"top-p sampling result: {dictionary[next_token]}")