Pytorch中的张量学习

关于`Pytorch`中的张量学习

张量的概念和创建

张量的概念

Tensor是pytorch中非常重要且常见的数据结构，相较于numpy数组，Tensor能加载到GPU中，从而有效地利用GPU进行加速计算。但是普通的Tensor对于构建神经网络还远远不够，我们需要能够构建计算图的 tensor，这就是 Variable。Variable 是对 tensor 的封装，主要用于自动求导。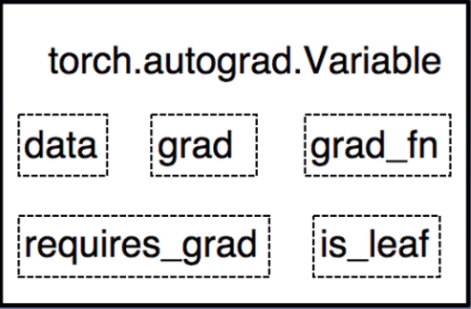

data：被包装的tensor
grad：data的梯度
grad_fn：创建tensor的function，是自动求导的关键
requires_grad：指示是否需要梯度
is_leaf：指示是否是叶子节点（用户创建的张量）

从pytorch 0.4.0开始，Variable并入了tensor，也就是这些属性直接存在于tensor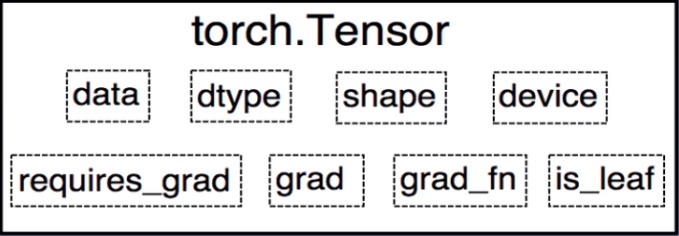

张量的创建

torch.tensor() ：从data创建tensor

data：数据，可以是list，Numpy
dtype：数据类型，默认与data一致
device：所在设备，cuda/cpu
requires_grad：是否需要梯度
pin_memory：是否存于锁页内存

torch.from_numpy()：从Numpy创建tensor
利用torch.from_numpy创建tensor与原ndarray共享内存，修改其中一个的数据，另一个也会改变。

torch.zeros()：以size创建全0张量

size：张量的形状，如(3, 3), (3, 224, 224)
out：输出的张量
layout：内存中的布局形式，有strided，sparse_coo等
device：所在设备,cuda/cpu
requires_grad：是否需要梯度

torch.zeros_like()：以输入张量的形状创建全0张量
torch.ones
torch.ones_like()

torch.full()：以size来创建指定数值的张量

size：张量的形状
fill_value：张量的值
torch.full_like()

torch.arange()：创建等差的1维张量

start：数列起始值
end：数列结束值（左闭右开）
step：数列公差，默认为1

torch.linspace()：创建均分的1维张量
注意事项：区间为[start, end]

start：数列起始值
end：数列结束值
steps：数列长度，步长=(end-start)/(steps-1)

torch.logspace()：创建对数均分的1维张量

start：数列起始值
end：数列结束值
steps：数列长度
base：对数函数的底，默认为10

torch.eye()：创建单位对角矩阵

torch.normal()：创建正太分布（高斯分布）

mean：均值
std：标准差
size：张量形状，当mean和std均为标量时需要设定

mean为标量，std为标量
mean为标量，std为张量
mean为张量，std为标量
mean为张量，std为张量

torch.randn():生成标准正太分布，即均值为0，标准差为1
torch.randn_like()

torch.rand()：在区间[0, 1)上生成均匀分布
torch.rand_like()

torch.randint()：在区间[low, high)生成整数均匀分布
torch.randint_like()

张量操作

张量的拼接和切分

torch.cat()和torch.stack()

torch.cat()：将张量按照维度dim进行拼接
torch.stack()：在新创建的维度dim上进行拼接

tensors：张量序列
dim：要拼接的维度

import torch
a = torch.ones((2, 3))
print(a)
tensor([[1., 1., 1.],
        [1., 1., 1.]])

t0 = torch.cat([a, a], dim=0)
print(t0)
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])

t1 = torch.cat([a, a], dim=1)
print(t1)
tensor([[1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.]])

torch.cat()是在原来的维度上进行拼接，假设针对二维张量，在第0维进行拼接就是增加行数，在第1维进行拼接则是增加列数。

t0 = torch.stack([a, a], dim=2)
print(t0)
print(t0.shape)
tensor([[[1., 1.],
         [1., 1.],
         [1., 1.]],
        [[1., 1.],
         [1., 1.],
         [1., 1.]]])
torch.Size([2, 3, 2])

t1 = torch.stack([a, a], dim=0)
print(t1)
print(t1.shape)
tensor([[[1., 1., 1.],
         [1., 1., 1.]],
        [[1., 1., 1.],
         [1., 1., 1.]]])
torch.Size([2, 2, 3])

torch.stack()是在新建的维度上进行拼接，假设针对二维张量，只有0维和1维，那么stack可以选择在第2维上进行拼接，拼接原理：
a的size为(2, 3)，第2维拼接，那么就需要给a增加第2维，即

1 2	[[[1.], [1.], [1.]], [[1.], [1.], [1.]]]

然后再把要拼接的张量按顺序添加到第2维中，即

1 2	[[[1., 1.], [1., 1.], [1., 1.]], [[1., 1.], [1., 1.], [1., 1.]]]

针对二维张量，只有0维和1维，如果stack选择在第0维进行拼接，那么就会将张量的原来两维后移，然后新建0维，拼接原理：
a的size为(2, 3)，新建第0维，即外面再加一层大括号

[
    [[1., 1., 1.],
    [1., 1., 1.]]
]

然后再把要拼接的张量添加到第0维中，即

[
    [[1., 1., 1.],
    [1., 1., 1.]],
    [[1., 1., 1.],
    [1., 1., 1.]]
]

torch.chunk()和torch.split()

torch.chunk()：将张量按维度dim进行平均切分
注意事项：若不能整除，最后一份张量小于其他张量，参数：

input：要切分的张量
chunks：要切分的份数

dim：要切分的维度

a = torch.rand((2, 5))
print(a)
tensor([[0.6590, 0.3914, 0.0760, 0.8725, 0.2828],
        [0.3575, 0.8045, 0.9501, 0.9880, 0.7684]])

print(torch.chunk(a, chunks=2, dim=1))
(tensor([[0.6590, 0.3914, 0.0760],
        [0.3575, 0.8045, 0.9501]]), 
tensor([[0.8725, 0.2828],
        [0.9880, 0.7684]]))

切分得到的张量维度大小计算：5(dim=1维度的大小)/2(chunks，切分的份数),结果向上取整

torch.split()：将张量按维度dim进行切分，参数

tensor：要切分的张量
split_size_or_sections：为int时，表示每一份的长度；为list时，按照list元素切分

dim要切分的维度

print(torch.split(a, 2, dim=1))
(
    tensor([[0.6590, 0.3914],
        [0.3575, 0.8045]]), 
    tensor([[0.0760, 0.8725],
        [0.9501, 0.9880]]), 
    tensor([[0.2828], [0.7684]])
)

print(torch.split(a, [2, 1, 2], dim=1))
(
    tensor([[0.6590, 0.3914],
        [0.3575, 0.8045]]), 
    tensor([[0.0760],[0.9501]]), 
    tensor([[0.8725, 0.2828],
        [0.9880, 0.7684]])
)

这里第2个参数指定为list时，其和应该等于要切分张量指定dim维度大小，否则会报错。

张量索引

torch.index_select()和torch.masked_select()
torch.index_select()：在维度dim上，按index索引数据
返回值：以index索引数据拼接的张量，参数

input：要索引的张量
dim：要索引的维度
index：要索引数据的序号

a = torch.randint(0, 9, size=(3, 3))
tensor([[0, 5, 1],
        [8, 0, 6],
        [2, 8, 5]])
# dtype必须设置为long类型
idx = torch.tensor([0, 2], dtype=torch.long)
torch.index_select(a, dim=0, index=idx)
tensor([[0, 5, 1],
        [2, 8, 5]])

torch.index_select(a, dim=1, index=idx)
tensor([[0, 1],
        [8, 6],
        [2, 5]])

torch.masked_select()：按mask中的True进行索引，返回一维张量，参数

input：要索引的张量

mask：与input同形状的布尔类型张量

mask = a.ge(5)
print(mask)
tensor([[False,  True, False],
        [ True, False,  True],
        [False,  True,  True]])
torch.masked_select(a, mask)
tensor([5, 8, 6, 8, 5])

ge表示greater than or equal，即大于等于
gt表示greater than，即大于
le表示less than or equal，即小于等于
lt表示less than，即小于

张量变换

`tensor.view()、torch.reshape()、torch.resize_()`

torch.view()可以调整tensor的形状，但必须保证调整前后元素总数一致。view不会修改自身的数据，返回的新tensor与原tensor共享内存，即更改一个，另一个也随之改变。

import torch

a = torch.arange(0,6).view(2, 3)
print(a)

tensor([[0, 1, 2],
        [3, 4, 5]])

b = a.view(-1, 2)  # 当某一维是-1时，会自动计算它的大小
print(b)

tensor([[0, 1],
        [2, 3],
        [4, 5]])

这里建议先看一下后面关于连续性的知识，torch.view()无法用于不连续的tensor，只有将不连续的tensor转化为连续的tensor（利用contiguous()），才能使用view()。

reshape() 和 view() 的区别：
（1）当 tensor 满足连续性要求时，reshape() = view()，和原来 tensor 共用存储区；
（2）当 tensor不满足连续性要求时，reshape() = **contiguous() + view()，会产生有新存储区的 tensor，与原来tensor 不共用存储区。

前面说到的 view()和reshape()都必须要用到全部的原始数据，比如你的原始数据只有12个，无论你怎么变形都必须要用到12个数字，不能多不能少。因此你就不能把只有12个数字的 tensor 强行 reshape 成 2×5 的。
但是 resize_() 可以做到，无论原始存储区有多少个数字，我都能变成你想要的维度，数字不够怎么办？随机产生凑！数字多了怎么办？就取我需要的部分！

截取时：会改变原tensor a，但不会改变storage（地址和值都不变），且a和b共用storage（这里是2638930351680
）。

import torch

# 原tensor a
a = torch.tensor([1,2,3,4,5,6,7])
print(a)
print(a.storage())
print(a.storage( ).data_ptr())
tensor([1, 2, 3, 4, 5, 6, 7])
 1
 2
 3
 4
 5
 6
 7
[torch.LongStorage of size 7]
2638930351680

# b是a的截取，并reshape成2×3
b = a.resize_(2,3)
print(a)
print(b)
tensor([[1, 2, 3],
        [4, 5, 6]])  # a变了
tensor([[1, 2, 3],
        [4, 5, 6]])

print(a.storage())
print(b.storage())
 1
 2
 3
 4
 5
 6
 7
[torch.LongStorage of size 7]
 1
 2
 3
 4
 5
 6
 7
[torch.LongStorage of size 7]

print(a.storage( ).data_ptr())
print(b.storage( ).data_ptr())
2638930352576
2638930352576

添加时：会改变原tensor a，且会改变storage（地址和值都变），但a和b还是共用storage（这里是2638924338752
）。

a = torch.tensor([1,2,3,4,5])
print(a)
print(a.storage())
print(a.storage( ).data_ptr())
tensor([1, 2, 3, 4, 5])
 1
 2
 3
 4
 5
[torch.LongStorage of size 5]
2638924334528

b = a.resize_(2,3)
print(a)
print(b)
tensor([[1, 2, 3],
        [4, 5, 0]])  # a变了
tensor([[1, 2, 3],
        [4, 5, 0]])

print(a.storage())
print(b.storage())
 1
 2
 3
 4
 5
 0
[torch.LongStorage of size 6]
 1
 2
 3
 4
 5
 0
[torch.LongStorage of size 6]

print(a.storage( ).data_ptr())
print(b.storage( ).data_ptr())
2638924338752
2638924338752

pytorch中实际还有torch.resize()方法，网上基本很少有介绍

`unsequeeze()和sequeeze()`

unsequeeze(dim)用来在维度dim上增加1维；sequeeze(dim)用来在dim上减少维度。

import torch

a = torch.tensor([[1, 2], [3, 4], [5, 6]])
print(a.size())
torch.Size([3, 2])

b = a.unsqueeze(0)  # 与unsqueeze(-3)等价，倒数第三维
c = a.unsqueeze(1)  # 与unsqueeze(-2)等价
d = a.unsqueeze(2)  # 与unsqueeze(-1)等价，倒数第一维，即第二维，也是最后一维
e = a.unsqueeze(3)  # 报错，提示dim的可选范围为[-3, 2]

# dim=0，在最外层加一维，即加一组[]
tensor([[[1, 2],
         [3, 4],
         [5, 6]]])

# dim=1, 进去一层[],然后加一维，即加[]且每遇到一个逗号，都加一组[]
tensor([[[1, 2]],
        [[3, 4]],
        [[5, 6]]])

# dim=2, 进去两层[],然后加一维，同样每遇到一个逗号，都加一组[]
tensor([[[1],
         [2]],
        [[3],
         [4]],
        [[5],
         [6]]])

sequeeze(dim)用来在dim上减少维度，但是如果指定的dim的size不等于1，是无法删掉维度的。

import torch

a = torch.tensor([[1, 2], [3, 4], [5, 6]])
print(a.squeeze(0))  # 删除无效，第0维，size为3
tensor([[1, 2],
        [3, 4],
        [5, 6]])

print(a.squeeze(1))  # 删除无效，第1维，size为2
tensor([[1, 2],
        [3, 4],
        [5, 6]])
# 与unsqueeze相似，这里dim的取值范围为[-2,1],-2与0等价，-1与1等价


a = torch.tensor([[1], [2], [3]])
a.squeeze(0)  # 删除无效，第0维，size为3
print(a.squeeze(1))  # 删除成功

tensor([1, 2, 3])

如果不指定要删除的dim，则删除所有size为1的维度

a = torch.tensor([[[1], [2], [3]]])
print(a.squeeze())

tensor([1, 2, 3])

`tensor.expand()`

参数为传入指定shape，在原shape数据上进行高维拓维，根据维度值进行重复赋值。

import torch

x = torch.tensor([1,2,3,4])
x.shape
torch.Size([4])

# x拓展一维，变1x4
x1 = x.expend(1,4)
print(x1)
tensor([[1, 2, 3, 4]])
print(x1.shape)
torch.Size([1, 4])

# x1拓展一维,增加2行，变2x4，多加的一行重复原值
x2 = x1.expend(2,1,4)
print(x2)
tensor([[[1, 2, 3, 4]],
        [[1, 2, 3, 4]]])
print(x2.shape)
torch.Size([2, 1, 4])

# x2拓展一维，增加2行，变为2x2x1x4,多加的一行重复原值
x3 = x2.expand(2,2,1,4)
print(x3) 
tensor([[[[1, 2, 3, 4]],

         [[1, 2, 3, 4]]],


        [[[1, 2, 3, 4]],

         [[1, 2, 3, 4]]]])
print(x3.shape)
torch.Size([2, 2, 1, 4])

# x直接拓展2个维度，变为2x1x4,
x4 = x.expand(2,1,4)
print(x4)

tensor([[[1, 2, 3, 4]],

        [[1, 2, 3, 4]]])

注意：

只能拓展维度，比如A的shape为2x4的，不能 A.expend(1,4)，只能保证原结构不变，在前面增维，比如A.expand(1,2,4)；
可以增加多维，比如x的shape为(4),x.expand(2,2,1,4)只需保证本身是4；
不能拓展低维，比如x的shape为(4)，不能x.expand(4,2)。

维度交换和转置

torch.transpose()和torch.t()，后者是前者的简化版本，当tensor的维度为2时，直接使用t()就是转置，当维度大于2时，则不能使用t()，要使用transpose()，且必须指定要交换的两个维度。

对于两维的tensor：

import torch

a = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(a.t())   # 转置

tensor([[1, 4],
        [2, 5],
        [3, 6]])

# 必须指定要交换的两个维度
print(a.transpose(1, 0))  # 等价于a.transpose(0, 1)

tensor([[1, 4],
        [2, 5],
        [3, 6]])

对于三维的tensor：

a = torch.tensor([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])

print(a)
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],
        [[ 7,  8,  9],
         [10, 11, 12]]])

print(a.transpose(0, 1))
tensor([[[ 1,  2,  3],
         [ 7,  8,  9]],
        [[ 4,  5,  6],
         [10, 11, 12]]])

print(a.transpose(0, 2))
tensor([[[ 1,  7],
         [ 4, 10]],
        [[ 2,  8],
         [ 5, 11]],
        [[ 3,  9],
         [ 6, 12]]])

print(a.transpose(1, 2))
tensor([[[ 1,  4],
         [ 2,  5],
         [ 3,  6]],
        [[ 7, 10],
         [ 8, 11],
         [ 9, 12]]])

如何理解三维张量的维度交换操作呢？可以把张量a每个元素的坐标列出来

(0, 0, 0), (0, 0, 1), (0, 0, 2)

(0, 1, 0), (0, 1, 1), (0, 1, 2)

(1, 0, 0), (1, 0, 1), (1, 0, 2)

(1, 1, 0), (1, 1, 1), (1, 1, 2)

a.transpose(0, 1)，以元素4为例，其坐标为(0, 1, 0)，交换0维和1维，则变为(1, 0, 0)，所以交换完成后元素4的位置坐标为(1, 0, 0)。

permute()方法与transpose方法的功能类似，但是其作用是让tensor按照指定维度顺序进行转置，其参数的个数就是张量的维度数。

当tensor为两维时

import torch

c = torch.tensor([[1, 2, 3], [4, 5, 6]])

print(c.permute(1, 0))  # 等价于.t()
tensor([[1, 4],
        [2, 5],
        [3, 6]])

# c.permute(0, 1)不会做任何改变

当tensor为三维时

import torch

a = torch.tensor([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])

print(a)
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],
        [[ 7,  8,  9],
         [10, 11, 12]]])

# 等价于transpose(0, 1)
print(a.permute(1, 0, 2))
tensor([[[ 1,  2,  3],
         [ 7,  8,  9]],
        [[ 4,  5,  6],
         [10, 11, 12]]])

# 等价于transpose(0, 2)
print(a.permute(2, 1, 0))
tensor([[[ 1,  7],
         [ 4, 10]],
        [[ 2,  8],
         [ 5, 11]],
        [[ 3,  9],
         [ 6, 12]]])

# 等价于transpose(1, 2)
print(a.permute(0, 2, 1))
tensor([[[ 1,  4],
         [ 2,  5],
         [ 3,  6]],
        [[ 7, 10],
         [ 8, 11],
         [ 9, 12]]])

除了上述这些转换方式，permute还可以permute(1, 2, 0)、

permute(2, 0,1)，也就是同时改变三个维度的顺序，所以permute的功能要比transpose更强大。

另外，还有a.T的用法，.T是permute的简化版本，其功能是把张量的维度逆序重新排列，假设一个tensor-a共有n维，a.T等价于a.permute(n-1, n-2, ..., 0)。

针对上述例子，c(二维张量), c.T与c.t()等价；a(三维张量), a.T与a.permute(2, 1, 0)等价。

张量的数学运算

加减乘除

torch.add()
torch.addcdiv()
torch.addcmul()
torch.sub()
torch.div()
torch.mul()

对数，指数，幂函数

torch.log()
torch.log10()
torch.log2()
torch.exp()
torch.pow()

三角函数

torch.abs()
torch.acos()
torch.cosh()
torch.cos()
torch.asin()
torch.atan()
torch.atan2()

torch.add()：逐元素计算 input + alpha x other，参数

input：第一个张量
alpha：乘项因子，默认为1
other：第二个张量

torch.addcdiv()：加法结合除法，参数

input：输入张量
value：乘项因子，默认为1
tensor1：除法运算的被除数
tensor2：除法运算的除数

out = input + value x (tensor1/tensor2)

torch.addcmul()：加法结合乘法，参数

input：输入张量
value：乘项因子，默认为1
tensor1：乘法运算的第一个张量
tensor2：乘法运算的第二个张量

out = input + value x tensor1 x tensor2

`torch.mul()与torch.mm()与torch.matmul()`

torch.mul(a, b) 是矩阵 a 和 b 对应位相乘，a 和 b的维度必须相等；torch.mm()是矩阵点乘，比如a的维度是(1, 2)，b的维度是(2, 3)，返回的就是(1, 3)的矩阵； torch.matmul()的用法比torch.mm更高级，torch.mm只适用于二维矩阵，而torch.matmul可以适用于高维。当然，对于二维的效果等同于torch.mm()。

`torch.max()与tensor.min()`

torch.max() 获取张量中的最大值（和索引），torch.min()获取张量中的最小值（和索引），两个方法用法完全一致，下面以max举例。

两个主要参数：input（张量）和dim（维度）

当输入张量为1维（即向量）：

import torch


a = torch.tensor([1, 2, 3, 4, 5, 6])
print(torch.max(a))  # 不指定dim，则仅返回最大值

tensor(6)

value, index = torch.max(a, dim=0)
print(value)
print(index)

tensor(6)  # 最大值
tensor(5)  # 最大值所在的索引

当输入张量为2维：

vec = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

print(torch.max(vec))  # 不指定dim，则仅返回张量中的最大值

tensor(12)

# dim=0，获取每一列的最大值和索引
value, index = torch.max(a, dim=0)
print(value)
print(index)

tensor([10, 11, 12])
tensor([3, 3, 3])

# dim=1，获取每一行的最大值和索引
value, index = torch.max(a, dim=1)
print(value)
print(index)

tensor([ 3,  6,  9, 12])
tensor([2, 2, 2, 2])

当输入张量为3维(这时候有点难理解啦，需要动脑思考，特别是需要立体思维想象)：

# 二维张量是一个平面，三维就看成多个平面叠加在一起
vec = torch.tensor([
    [[7, 2, 3], [4, 11, 6]],
    [[1, 8, 9], [10, 5, 12]]
])

# dim=0，就是获取不同平面上同一位置，值最大的一个（3D空间想象起来）
value, index = torch.max(vec, dim=0)
print(value)
print(index)

tensor([[ 7,  8,  9],
        [10, 11, 12]])
tensor([[0, 1, 1],
        [1, 0, 1]])

# dim=1，(1)、先单独看一个平面，相当于二维张量时，dim=0，即获取同一平面内每一列的最大值；(2)、与(1)类似，获取每一个平面内每一列的最大值
value, index = torch.max(vec, dim=1)
print(value)
print(index)

tensor([[ 7, 11,  6],
        [10,  8, 12]])
tensor([[0, 1, 1],
        [1, 0, 1]])

# dim=2, (1)、先单独看一个平面，相当于二维张量时，dim=1，即获取同一平面内每一行的最大值；(2)、与(1)类似，获取每一个平面内每一行的最大值
value ,index = torch.max(vec, dim=2)
print(value)
print(index)

tensor([[ 7, 11],
        [ 9, 12]])
tensor([[0, 1],
        [2, 2]])

当输入张量为4维，那就不想了…

`tensor.sum()和torch.mean()`张量求和、求平均

其实与torch.max()非常相似，一维张量求和没啥好说的，二维张量如果不指定dim参数则是求所有元素的和，dim=0是求每一列的和，dim=1则是求每一行的和。

import torch

a = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(a.sum())
tensor(21)

print(a.sum(dim=0))
tensor([5, 7, 9])

print(a.sum(dim=1))
tensor([ 6, 15])

当张量为3维时，与上面一样想象一下3D空间

# 二维张量是一个平面，三维就看成多个平面叠加在一起
vec = torch.tensor([
    [[7, 2, 3], [4, 11, 6]],
    [[1, 8, 9], [10, 5, 12]]
])
# dim=0，就是将不同平面上同一位置的元素累加起来
print(vec.sum(dim=0))
tensor([[ 8, 10, 12],
        [14, 16, 18]])

# dim=1,(1)、先单独看一个平面，相当于二维张量时，dim=0，即计算同一平面内每一列的和；(2)、与(1)类似，计算每一个平面内每一列的和
print(vec.sum(dim=1))
tensor([[11, 13,  9],
        [11, 13, 21]])

# dim=2,(1)、先单独看一个平面，相当于二维张量时，dim=1，即计算同一平面内每一行的和；(2)、与(1)类似，计算每一个平面内每一行的和
print(vec.sum(dim=2))
tensor([[12, 21],
        [18, 27]])

torch.mean()是求平均值，有一点要求是张量的类型为float类型，其他的与torch.sum()基本是一致的。

其他张量操作

`tensor.item()`与`tensor.tolist()`

item()是将一个张量的值，以一个python数字形式返回，但该方法只能包含一个元素的张量，对于包含多个元素的张量，可以使用tolist()方法。

import torch

b = torch.tensor([1])
print(b.item())  # 输出为：1

c = torch.tensor([1, 2, 3])
print(c.tolist())  # 输出为：[1, 2, 3]

`tensor.is_contiguous()、tensor.contiguous()`

在pytorch中，tensor的实际数据是以一维数组（storage）的方式存于某个连续的内存中的。而且，pytorch的tensor是以“行优先”进行存储的。

所谓tensor连续（contiguous），指的是tensor的storage元素排列顺序与其按行优先时的元素排列顺序相同。如下图所示：

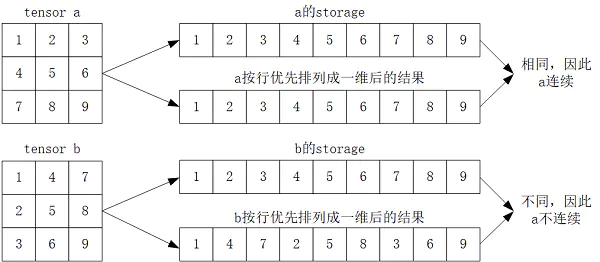
之所以会出现不连续现象，本质上是由于pytorch中不同tensor可能共用同一个storage导致的。

pytorch的很多操作都会导致tensor不连续，比如tensor.transpose()、tensor.narrow()、tensor.expand()。

以转置为例，因为转置操作前后共用同一个storage，但显然转置后的tensor按照行优先排列成1维后与原storage不同了，因此转置后结果属于不连续。

import torch

a = torch.tensor([[1,2,3],[4,5,6]])
print(a)
tensor([[1, 2, 3],
        [4, 5, 6]])
print(a.storage())
 1
 2
 3
 4
 5
 6
[torch.LongStorage of size 6]
print(a.is_contiguous())  # a是连续的
True

b = a.t()  # b是a的转置
print(b)
tensor([[1, 4],
        [2, 5],
        [3, 6]])
print(b.storage())
 1
 2
 3
 4
 5
 6
[torch.LongStorage of size 6]
print(b.is_contiguous())  # b是不连续的
False

# 之所以出现b不连续，是因为转置操作前后是共用同一个storage的
print(a.storage().data_ptr())
print(b.storage().data_ptr())
2638924341056
2638924341056

tensor.contiguous()返回一个与原始tensor有相同元素的 “连续”tensor，如果原始tensor本身就是连续的，则返回原始tensor。

import torch

c = b.contiguous()

# 形式上两者一样
print(b)
print(c)
tensor([[1, 4],
        [2, 5],
        [3, 6]])
tensor([[1, 4],
        [2, 5],
        [3, 6]])

# 显然storage已经不是同一个了
print(b.storage())
print(c.storage())
 1
 2
 3
 4
 5
 6
[torch.LongStorage of size 6]
 1
 4
 2
 5
 3
 6
[torch.LongStorage of size 6]

# b不连续，c是连续的
print(b.is_contiguous())
False
print(c.is_contiguous())
True

# 此时执行c.view()不会出错
c.view(2,3)
tensor([[1, 4, 2],
        [5, 3, 6]])

关于Pytorch中的张量学习