Pytorch中权值初始化和损失函数
权值初始化
梯度消失与爆炸
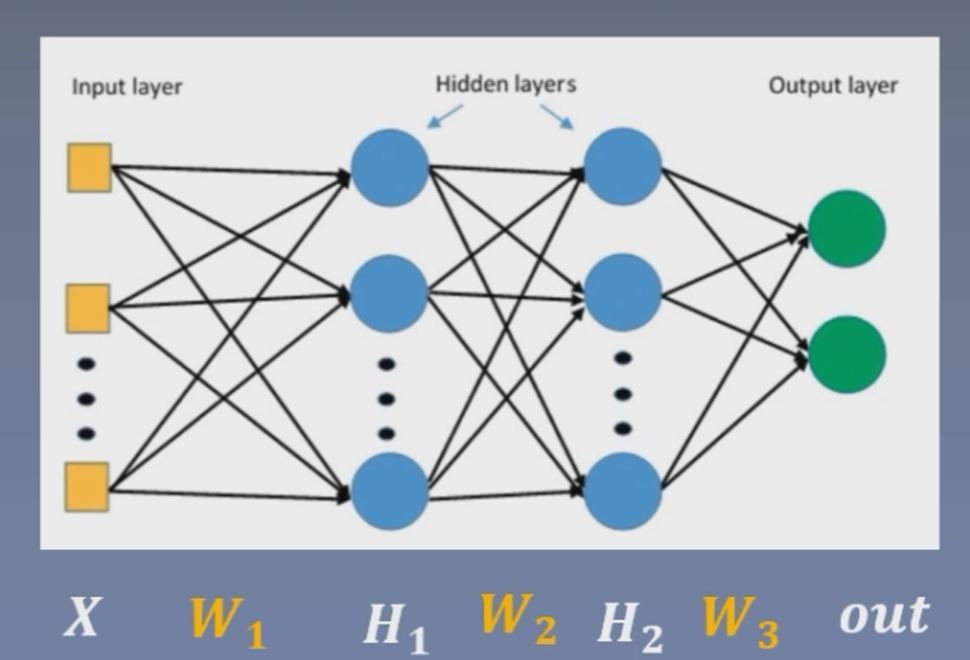
针对上面这个两个隐藏层的神经网络,我们求w2的梯度

可以发现,w2的梯度与H1(上一层网络的输出)有很大的关系,当h1趋近于0时,w2的梯度也趋近于0,当h1趋近于无穷大时,w2的梯度也趋近于无穷大。
一旦发生梯度消失或梯度爆炸,那么网络将无法训练,为了避免梯度消失或梯度爆炸的出现,需要控制网络输出值的范围(不能太大也不能太小)
使用下述代码举例,可以发现网络在第30层时,网络的输出值就达到了无穷大
1 | import torch.nn as nn |
下面我们通过方差公式推导这一现象出现的原因:
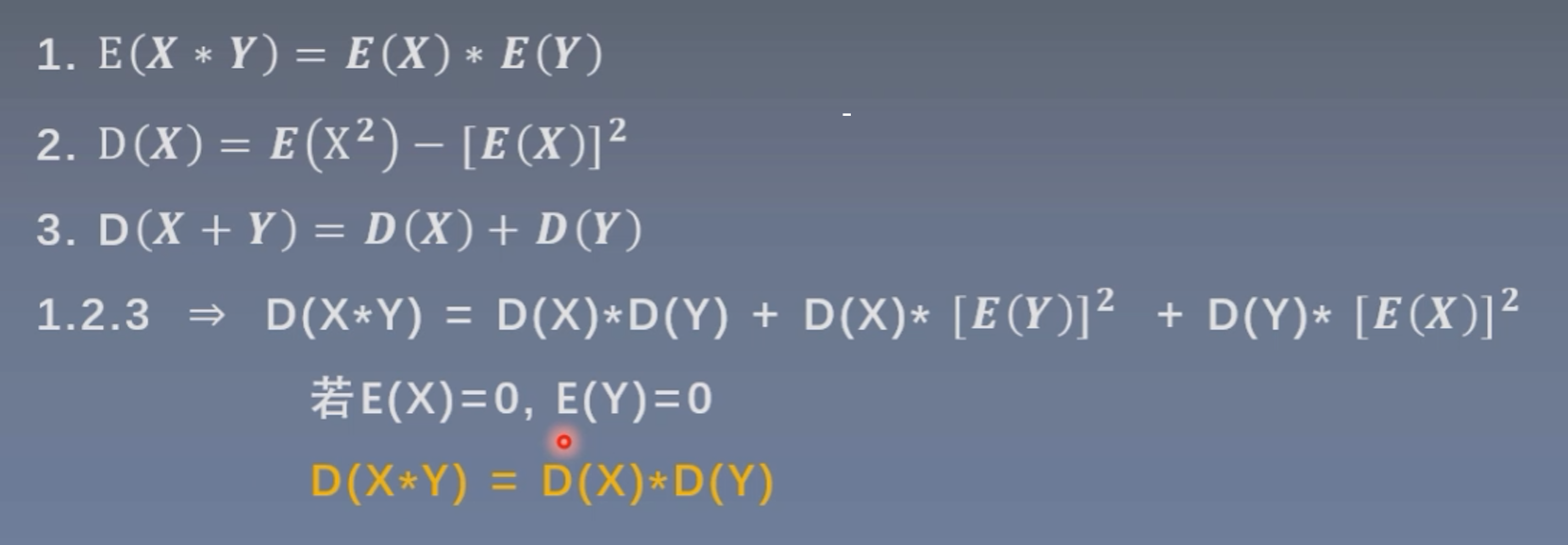
X和Y表示相互独立的两个变量,且符合均值为0(期望也为0),标准差为1的分布;E表示期望,D表示方差。
关于图中公式的推导参考文章:https://zhuanlan.zhihu.com/p/546502658
最后的结论是:两个独立的变量X和Y,他们乘积的方差/标准差=各自的方差/标准差的乘积。
那么我们把这个结论运用到神经网络隐藏层的神经元运算中
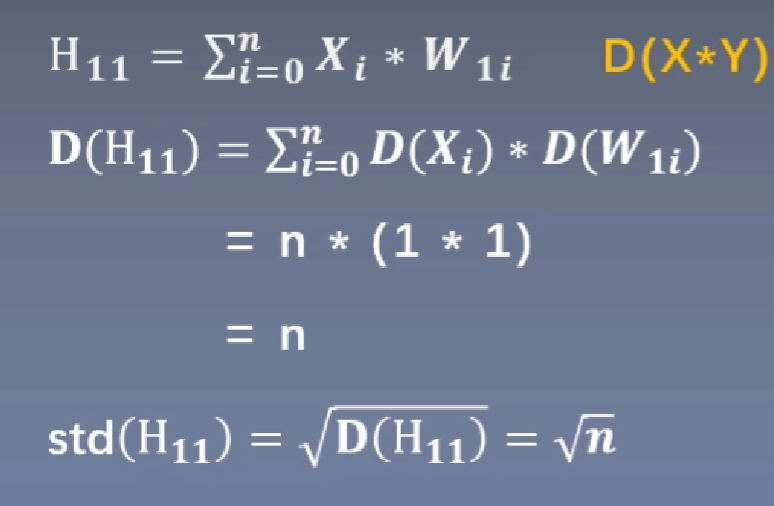
第一个的隐藏层的神经元输出值的方差为输入值的n倍(n是输入层神经元数量),第二隐藏层的方差则是第一隐藏层的n倍,以此类推。
其实通过公式推导我们发现,下一层神经元的输出值方差与三个因素有关,(1)每一层神经元的数量;(2)输入值x的方差;(3)权重矩阵W的方差。
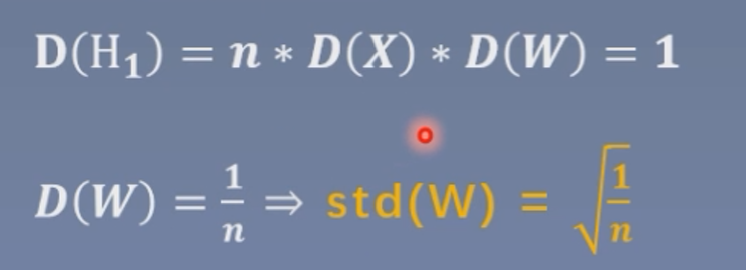
如果想要控制神经元的输出值方差为1,我们可以保证X的方差为1,若想要消掉n,那就是要W的方差为1/n。
我们在代码中加上这一操作
1 | def initialize(self): |
这时候每一层的网络输出值就会是1左右,不会变成无限大了。
Xavier初始化
在上述例子中,我们并未考虑到激活函数,假设我们在forward中添加激活函数再来观察输出。
1 | def forward(self, x): |
可以看到随便网络的增加,其输出值越来越小,最终可能会导致梯度的消失。Xavier初始化方法就是针对有激活函数时,网络应该如何初始化,是的每一层网络层的输出值方差为1。

n(i)表示第i层网络神经元的个数,n(i+1)表示第i+1层网络神经元的个数;
权重矩阵W符合均匀分布,其分布的范围是[-a, a],方差等于(下限-上限)的平方除以12,从而最终可以用神经元个数来表示a。
我们下面在代码中来实现这一初始化方法
1 | def initialize(self): |
现在每一层网络的输出值就不会越来越小了。
pytorch中提供了进行Xavier初始化的方法
1 | nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain) |
Kaiming初始化
Xavier只适合于饱和激活函数,而非饱和激活函数如relu则不适用
假设针对上面的代码,我们把激活函数换成relu:
1 | def forward(self, x): |
可以看到网络的输出值不断增大,有可能会导致梯度爆炸。
Kaiming初始化方法则是用来解决非激活函数。

其中a是针对relu的变种其负半轴的斜率。
针对上述代码,我们改用Kaiming初始化
1 | # Kaiming初始化 |
pytorch中同样有直接Kaiming初始化的方法
1 | nn.init.kaiming_normal_(m.weight.data) |
nn.init.calculate_gain
主要功能:计算激活函数的方差变化尺度
主要参数:
- nonlinearity:激活函数名称
param:激活函数的参数,如Leaky Relu的negative_slop
1 | x = torch.randn(10000) |
也就是说数据经过tanh之后,其标准差会减小1.6倍左右。
损失函数
损失函数概念
衡量模型输出与真实标签的差异

损失函数一般指单个样本,而代价函数则是所有样本,目标函数既包括代价函数(尽可能的小),也包括一个正则项,也就是避免过拟合。
pytorch中的loss
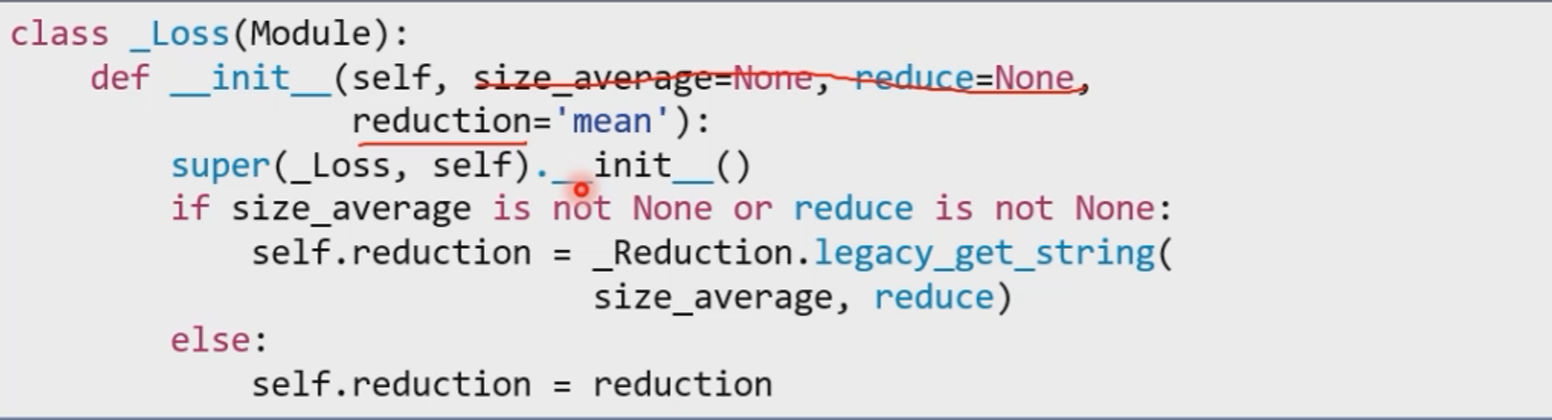
size_average和reduce参数即将废弃,不要使用。
nn.CrossEntropyLoss
功能:nn.LogSoftmax()与nn.NLLLoss()结合,进行交叉熵计算
参数:
- weight:各类别的loss设置权值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
none:逐元素计算
sum:所有元素求和,返回标量
mean:加权平均,返回标量
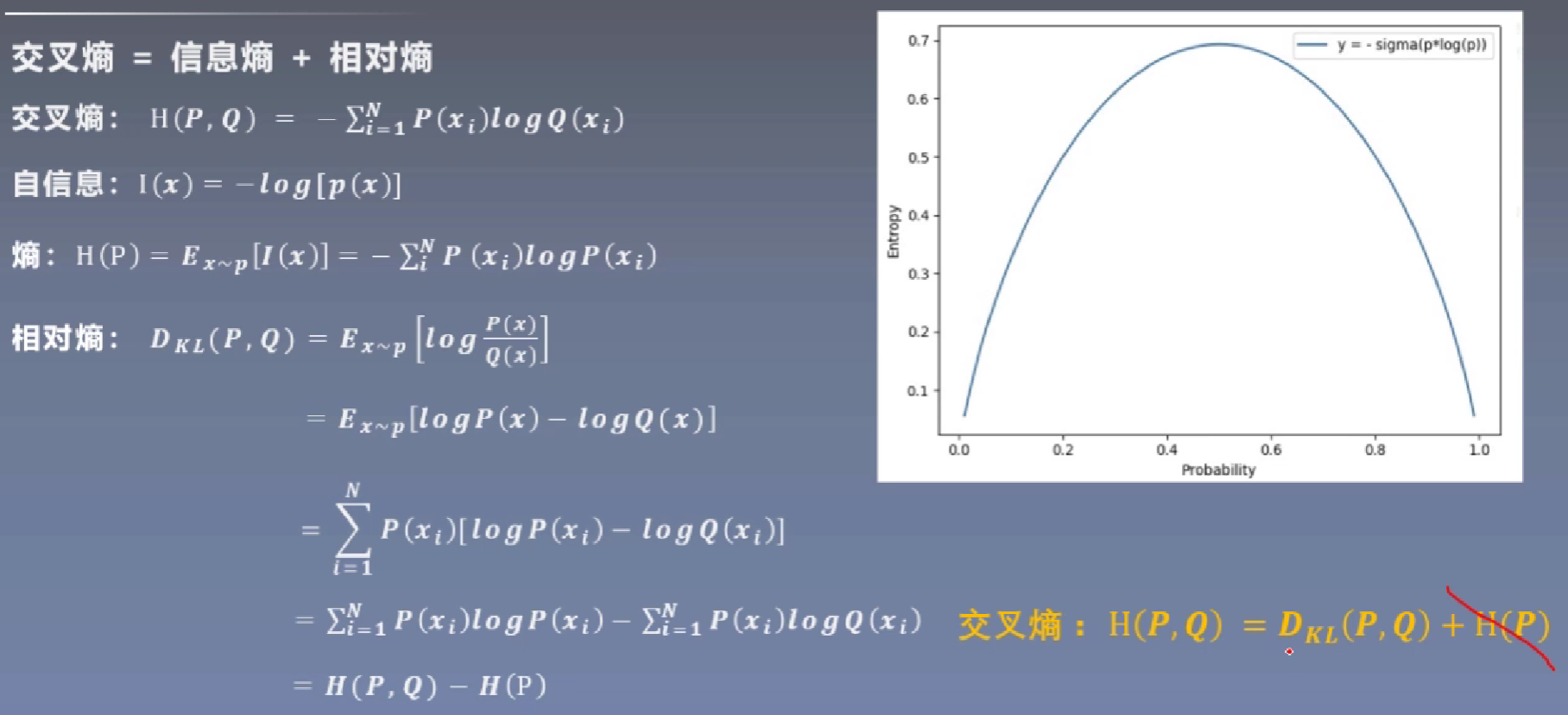
P表示训练集标签,Q表示预测值标签;
熵就是对自信息求期望。H(P)表示训练集标签的熵,其为定值。

这里x是神经元的输出,class表示该输出所对应的类别。
第一个式子是未设置weight参数的形式,第二个式子是设置了weight的形式。
Pytorch代码(未设置weight)
1 | import torch |
Pytorch代码(设置weight)
1 | weights = torch.tensor([1, 2], dtype=torch.float) |
因为给不同的类别设置了权重,这里类别0的权重为1,类别1的权重设置为2,所以针对第一个输出值的类别为0,其损失乘以1,依然是1.3133;第二、三个输出值的类别为1,其损失乘以2。
当reduction=’sum’时,就是把这几些损失加在一起;
当reduction=’mean’时,求和之后除以总份数(1+2+2=5)。
如果将weight改为[0.7, 0.3],输出则为
1 | weights: tensor([0.7000, 0.3000]) |
对于none和sum的形式,weight是比较好理解的,对于mean的形式,我们来手动计算一下
1 | # compute by hand |
nn.NLLLoss
功能:实现负对数似然函数中的负号功能
主要参数:
- weight:各类别的loss设置权值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
1 |
|
这里神经网络的输出分别为x1=[1, 2]、x2=[1, 3]、x3=[1, 3],其中第一个输出对应类别为0,所以loss是对其x1[0]取反,得到-1;同理第二、三个输出对应类别为1,所以loss是对其x2[1]和x3[1]取反,得到-3。
注意:这里的只有两个类别0和1,所以输出的x长度也是为2,这是互相对应的,如果有三类,则输出x的长度为3。
这里x1、x2、x3可以看作是不同样本输出,而x1内部的[1,2]可以看作是不同神经元的输出。
nn.BCELoss
功能:二分类交叉熵,输入值取值在[0,1]
主要参数:
- weight:各类别的loss设置权值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean

1 | # BCELoss |
1 | # compute by hand |
nn.BCEWithLogitsLoss
功能:结合Sigmoid与二分类交叉熵
注意事项:网络最后不加sigmoid函数
主要参数:
pos_weight:正样本的权值(正样本的数量乘以pos_weight)- weight:各类别的loss设置权值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
1 | # BCE with logis Loss |
可以看到这里与BCELoss相比,输入并没有进行sigmoid,最后计算的损失是与BCELoss一致的。
下面是关于pos_weight参数的理解
1 | # BCE with logis Loss |
这里第1个样本、第2个样本的第1个神经元,第3个样本、第4个样本的第2个神经元的输出类别为1(正样本),所以其损失值会乘以pos_weight的值,即0.3133 * 3 = 0.9398。
nn.L1Loss
功能:计算inputs与target之差的绝对值
nn.MSELoss
功能:计算inputs与target之差的平方
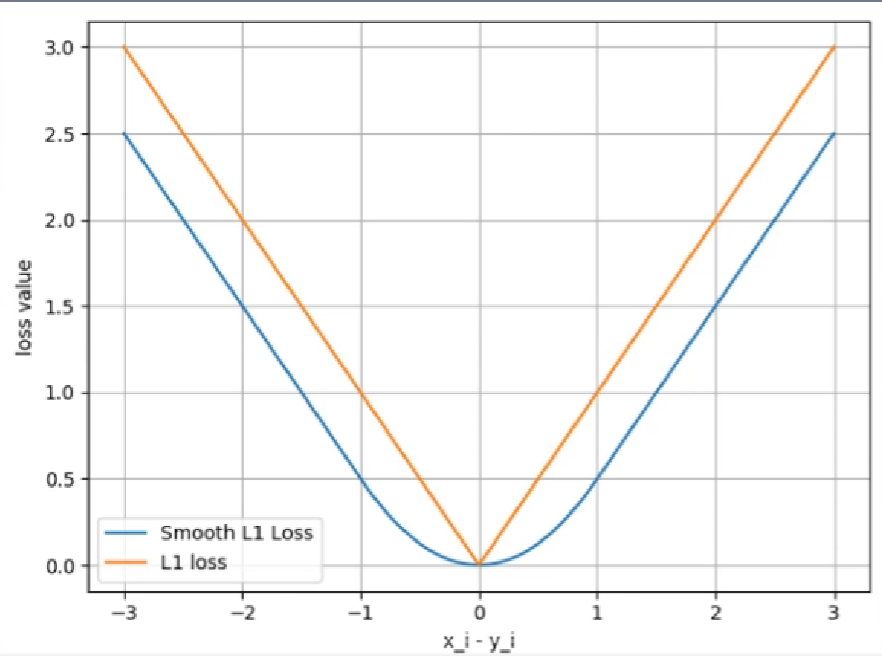
nn.SmoothL1Loss
功能:平滑的L1Loss
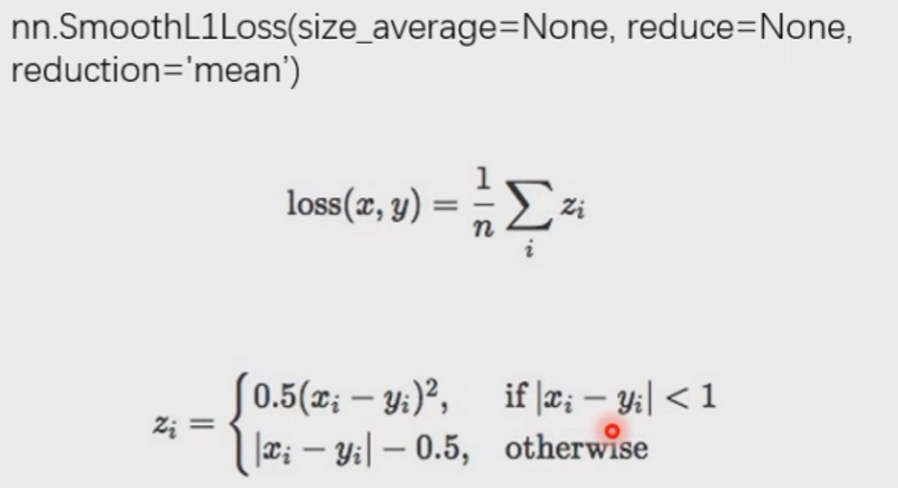
nn.PoissonNLLLoss
功能:泊松分布的负对数似然损失函数
nn.KLDivLoss
nn.MarginRankingLoss
功能:计算两个向量之间的相似度,用于排序任务
特别说明:该方法计算两组数据之间的差异,返回一个n*n的loss矩阵
主要参数:
- margin:边界值,x1与x2之间的差异值
- reduction:计算模式,可为none/sum/mean
y=1时,希望x1比x2大,当x1>x2时,不产生loss
y=-1时,希望x2比x1大,当x2>x1时,不产生loss
1 | # Margin Ranking Loss |
这里损失函数分别计算x1每个元素与x2所有元素之间的损失,所以得到一个3x3的矩阵,当x1的第一个元素[1]与x2计算损失时,y分别为[1, 1, -1],即1<2,与期望的x1>x2不符,损失=2-1=1,与期望x1<x2相符时,则不产生损失(损失为0)。
nn.MultiLabelMarginLoss
多标签:一个样本可能对应多个类别
功能:多标签边界损失函数
nn.SoftMarginLoss
功能:计算二分类的logistic损失
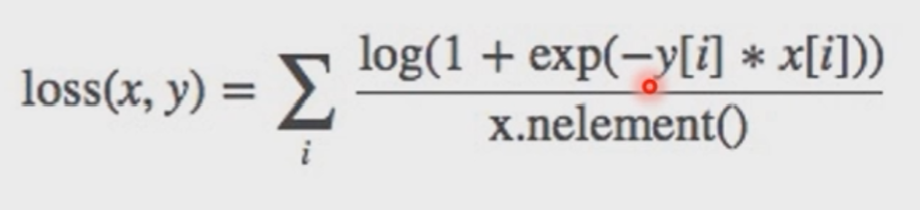
1 | # SoftMargin Loss |
nn.MultiLabelSoftMarginLoss
功能:SoftMarginLoss多标签版本
nn.MultiMarginLoss
功能:计算多分类的折页损失
nn.TripletMarginLoss
功能:计算三元组损失,人脸验证中常用
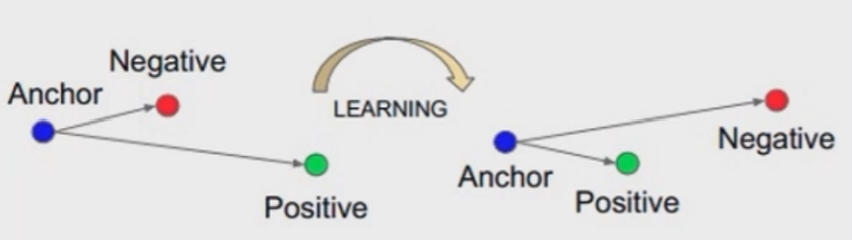
主要是为了使anchor与positive离得更近,anchor与negative离得更远。
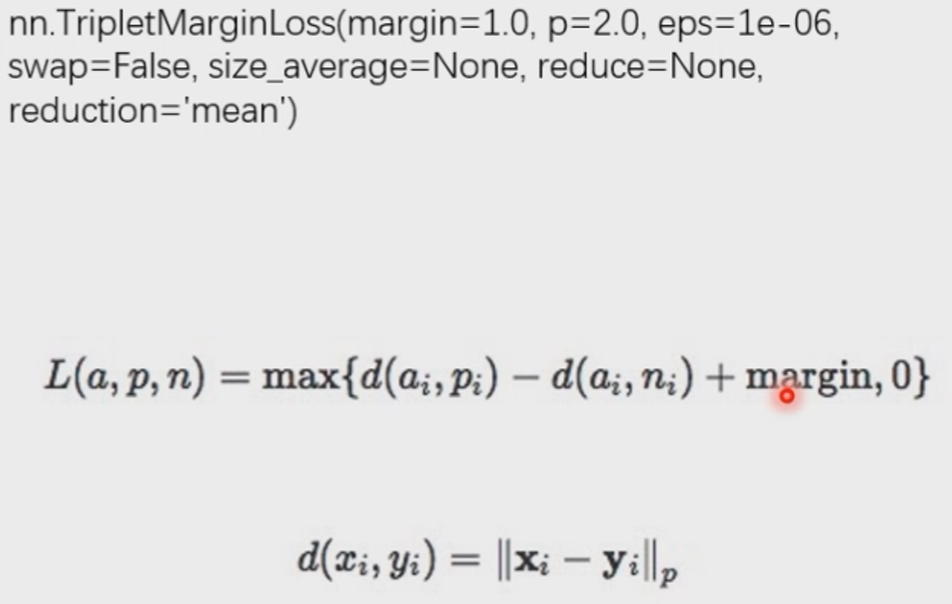
1 | # Triplet Margin Loss |
nn.HingeEmbeddingLoss
功能:计算两个输入的相似性,常用于非线性embedding和半监督学习
特别注意:输入x应为两个输入之差的绝对值

1 | # Hinge Embedding Loss |
三角号代表margin参数
nn.CosineEmbeddingLoss
功能:采用余弦相似度计算两个输入的相似性
主要参数:
- margin:可取值[-1, 1],推荐为[0, 0.5]
- reduction:计算模式,可为none/sum/mean

1 | # Cosine Embedding Loss |
1 | # compute by hand |
nn.CTCLoss
功能:计算CTC(Connectionist Temporal Classification)损失,解决时序类数据的分类(比如OCR)。
主要参数:
blank:blank label- zero_infinity:无穷大的值或梯度置0
- reduction:计算模式,可为none/sum/mean