使用BiLSTM-CRF进行命名实体识别

发表于 | 分类于

使用BiLSTM-CRF进行命名实体识别

BiLSTM-CRF网络结构

关于LSTM的原理以及其对比RNN的优势前面已经有多篇文章介绍了，这里就不再赘述。


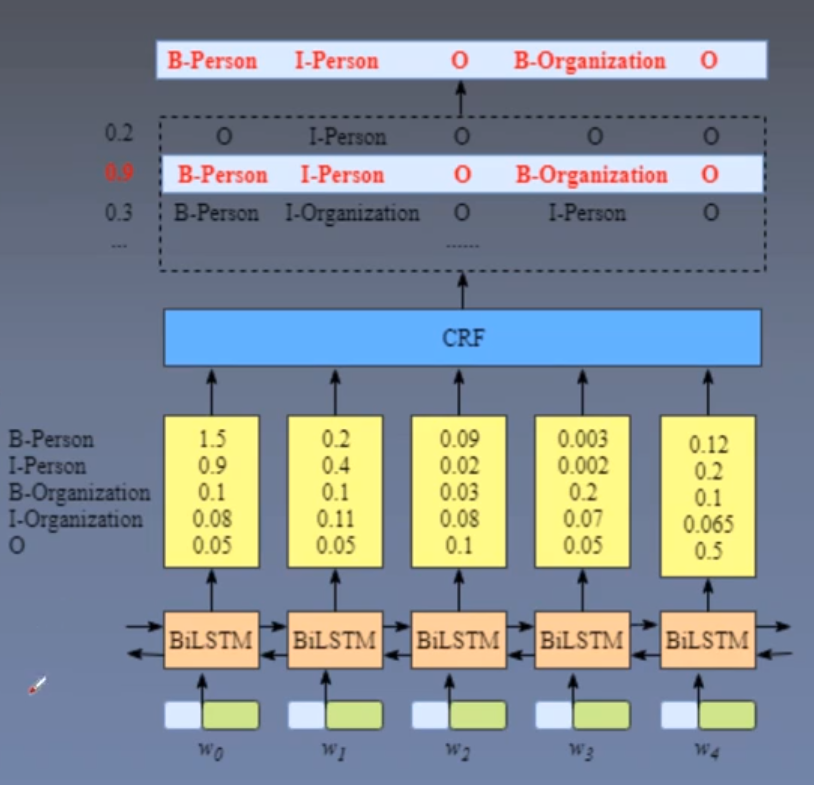
使用BiLSTM-CRF进行命名实体识别任务时的步骤流程（粗略地）：

  1. 先将句子转化为字词向量序列，字词向量可以在事先训练好或随机初始化，在模型训练时还可以再训练；
  2. 经BiLSTM特征提取，输出是每个单词对应的预测标签；
  3. 经过CRF层约束，输出最优标签序列。

使用BiLSTM-CRF进行命名实体识别任务时的步骤流程（细致地）：

  1. 先将字词传入Embedding层获取词向量，然后传入BiLSTM层之后得到隐状态；
  2. 将完整的隐状态序列接入线性层，从n维映射到k维，其中k是标注集的标签数；
  3. 从而得到自动提取的句子特征，记作矩阵P = (p1, p2, …, pn)，注意该矩阵是非归一化矩阵
    其中pi表示该单词对应各个类别的分数；
  4. 如果没有CRF层，预测输出根据每个词对应类别的最大值作为输出类别，最后通过多分类交叉熵计算损失进行反向传播；如果有CRF层，通过转移矩阵校正发射分数，然后接5、6；
  5. 通过维特比解码算法获取最优路径，即获取最优标签序列；
  6. 计算CRF Loss进行反向传播。

如上图中所示，BiLSTM的输出矩阵（第一列）1.5(B-Person), 0.9(I-Person), 0.1(B-Organization), 0.08(I-Organization),这些分数将是CRF层的输入。

该矩阵对应的值叫做发射分数，用Xiyj代表发射分数，i是单词的位置索引，yj是类别的索引。
例如这里Xi=1,yj=2代表w1单词的B-Organization的发射分数，即
X(w1,B-Organization=0.1)。

这里通过BiLSTM和全连接层已经得到了每个单词对应到各个类别的分数，那么不就取分数最高的类别不就可以了吗，正常情况下当然是可以的，但是会有一些非正常的情况，例如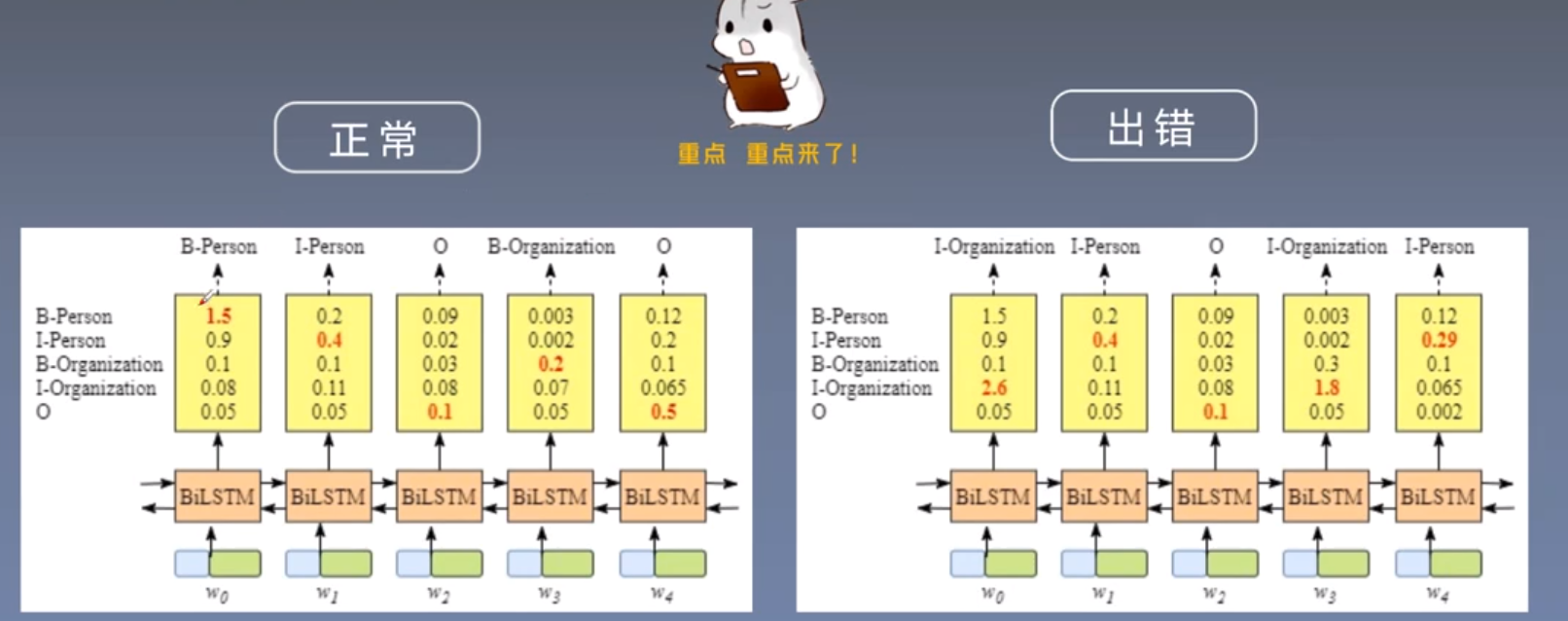

在上图的右侧部分，w0单词分数最大的类别是I-Organization，而I-Organization表示的是组织机构的内部，而w0是第一个单词，所以明显不合理，然后I-Person跟在I-Organization后面也是不合理的，根据BIO标注规则，可以得到以下结论：

  1. 句子的开头应该是“B-”或“O”，而不是“I-”。
  2. “B-label1 I-label2 I-label3…”，在该模式中，类别1,2,3应该是同一种实体类别。比如，“B-Person I-Person” 是正确的，而“B-Person I-Organization”则是错误的。
  3. “O I-label”是错误的，命名实体的开头应该是“B-”而不是“I-”。

如果不了解NER的标注规则，如BIO标注的，要先去学习下

但是这一结论，神经网络是不知道的，所以可能会出现图右侧的情况，这就是CRF约束层的作用。

CRF层通过转移分数来校正发射分数中不合理的地方，转移矩阵是BiLSTM-CRF模型的一个参数，可随机初始化转移矩阵的分数，然后在训练中更新。


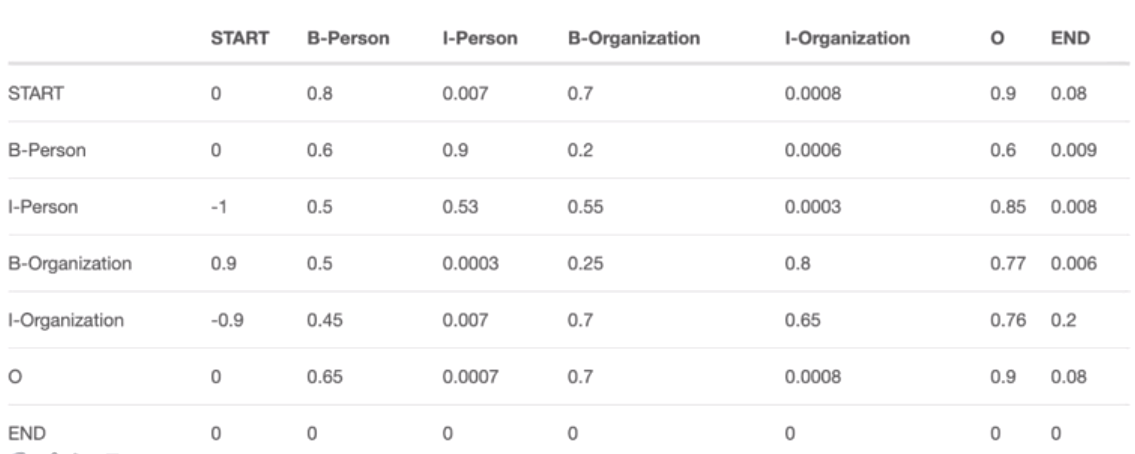
图中每一行表示每个标签转移到其他标签的概率，例如第一行，Start转移到B-Person和B-Organization的概率分别为0.8和0.7，表示概率较大，转移到I-Person和I-Organization的概率分别为0.007和0.0008，概率较小（基本不可能），然后将发射分数+转移分数得到打分之和，然后再取最高的分数。

在具体实现时，还有一个叫做路径分数的东西，其就是发射分数+转移分数之和，我们取路径分数最大的一条路径就是最佳标签序列。

CRF损失函数&维特比解码（Viterbi算法）

算法定义：一种用以选择最优路径的动态规划算法，从开始状态后每走一步，记录到达该状态所有路径的最大概率值，最后以最大值为基准继续向后推进，最后再从结尾回溯最大概率，也就是最有可能的最优路径。

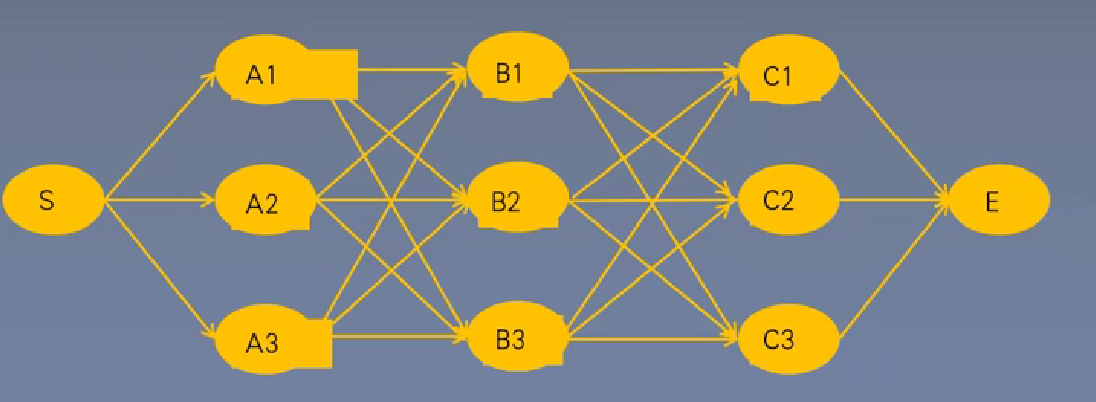
设有N个状态，序列长度为T，因为穷举法是每个时间步都有T种选择，而维特比只需要关注每两个时间步的选择（不需要关注前面的时间步）。

那么穷举法的时间复杂度为N的T次方，而维特比算法的时间复杂度为TxN的平方。

因为在实际任务种，T（序列长度）一般远大于N（类别数量），所以维特比算法的效率更高。

CRF Loss：计算真实路径得分与所有路径得分的比值，CRF损失函数由两部分组成，真实路径的分数和所有路径的总分数，真实路径的分数应该是所有路径中分数最高的。而损失函数是要求loss最小，所以使用负Log函数。

真实路径得分是指标注数据的路径分数

计算当前节点得分的方法

类似维特比解码算法，这里每个节点记录之前所有节点到当前节点的路径总和，最后一步即可得到所有路径的总和。

图中假设有共有两种类别（1和2），共有两个时间步（0时间步和1时间步），previous中的x01代表0时间步类别为1的值，x02代表1时间步类别为2的值，因为是previous可以想象成这个节点之前所有节点到当前节点的路径总和。

obs中的x11代表1时间步类别为1的值，x12代表1时间步类别为2的值，可以理解为发射分数。

而t11代表从上个时间步的1类别转移到当前时间步1类别的转移分数，t12，t21，t22同理。

计算所有路径得分的方法

这里计算从时间步0到时间步1的所有路径得分，因为previous本身就是计算到当前时间步的所有路径得分，所以最后更新previous。

预测

使用PyTorch实现BiLSTM-CRF

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
# coding=utf-8
# https://pytorch.org/tutorials/beginner/nlp/advanced_tutorial.html
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.optim as optim

torch.manual_seed(1)


def argmax(vec):
    # 获取vec第1维上的最大值（当vec为矩阵时，就是每一行的最大值），分别返回相应的值和索引
    _, idx = torch.max(vec, 1)
    return idx.item()  # 返回张量中的值，张量中只有一个值时，使用.item()，多个值时使用.list()


def prepare_sequence(seq, to_ix):
    """
    获取传入文本在词典中的序号
    :param seq: 传入分割好的文本，以列表形式
    :param to_ix: 单词/词语 到 序号的映射字典
    :return:
    """
    idxs = [to_ix[w] for w in seq]
    return torch.tensor(idxs, dtype=torch.long)


def log_sum_exp(vec):
    """
    前向算法时不断累积之前的结果，这样就会有个缺点
    指数和累积到一定程度后，会超过计算机浮点值的最大值，变成inf，这样取log后也是inf
    为了避免这种情况，用一个合适的值clip去提取指数和的公因子，这样就不会某项变得过大而无法计算
    sum = log(exp(s1) + exp(s2) + ... + exp(s100))
        = log(exp(clip) + exp(s1-clip) + exp(s2-clip) + ... + exp(s100-clip))
        = clip + log(exp(s1-clip) + exp(s2-clip) + ... + exp(s100-clip))
    :param vec:
    :return:
    """
    max_score = vec[0, argmax(vec)]
    # 将最大值广播
    max_score_broadcast = max_score.view(1, -1).expand(1, vec.size()[1])
    return max_score + torch.log(torch.sum(torch.exp(vec - max_score_broadcast)))


class BiLSTM_CRF(nn.Module):

    def __init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_dim):
        super(BiLSTM_CRF, self).__init__()
        self.embedding_dim = embedding_dim  # 词向量维度（长度），即用多少维度向量表示一个词
        self.hidden_dim = hidden_dim
        self.vocab_size = vocab_size  # 词表大小
        self.tag_to_ix = tag_to_ix    # 标签序号的映射字典
        self.tagset_size = len(tag_to_ix)  # 标签数量/类别数

        # 词嵌入层，size为(词表大小, 词向量维度)
        self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
        # 因为这里LSTM是双向的，input_size是词向量维度，隐藏层特征大小是hidden_dim//2
        self.lstm = nn.LSTM(embedding_dim, hidden_dim // 2, num_layers=1, bidirectional=True)

        # 将BiLSTM提取的特征向量映射到特征空间，即经过全连接得到发射分数
        self.hidden2tag = nn.Linear(hidden_dim, self.tagset_size)

        # 转移矩阵的参数初始化，transitions[i, j]代表的是从j个tag转移到第i个tag的转移分数（这个点很重要）
        self.transitions = nn.Parameter(
            torch.randn(self.tagset_size, self.tagset_size))

        # 初始化所有其他tag转移到START_TAG的分数非常小，即不可能由其他tag转移到START_TAG
        # 初始化STOP_TAG转移到所有其他tag的分数非常小，即不可能由STOP_TAG转移到其他tag
        # print(self.transitions.data)
        self.transitions.data[tag_to_ix[START_TAG], :] = -10000
        # print(self.transitions.data)
        self.transitions.data[:, tag_to_ix[STOP_TAG]] = -10000
        # print(self.transitions.data)

        self.hidden = self.init_hidden()

    def init_hidden(self):
        # 初始化LSTM的参数
        return (torch.randn(2, 1, self.hidden_dim // 2),
                torch.randn(2, 1, self.hidden_dim // 2))

    def _get_lstm_features(self, sentence):
        self.hidden = self.init_hidden()
        # print(self.word_embeds(sentence), self.word_embeds(sentence).size())
        # 先获取词向量，然后相当于增加了一个维度
        embeds = self.word_embeds(sentence).view(len(sentence), 1, -1)
        # 然后传入LSTM，
        lstm_out, self.hidden = self.lstm(embeds, self.hidden)
        lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
        # lstm_features其实就是发射分数
        lstm_feats = self.hidden2tag(lstm_out)
        return lstm_feats

    def _score_sentence(self, feats, tags):
        # 计算给定tag序列的分数，即一条路径的分数
        score = torch.zeros(1)
        tags = torch.cat([torch.tensor([self.tag_to_ix[START_TAG]], dtype=torch.long), tags])
        for i, feat in enumerate(feats):
            # 递推计算路径分数：转移分数+发射分数
            score = score + self.transitions[tags[i + 1], tags[i]] + feat[tags[i + 1]]
        score = score + self.transitions[self.tag_to_ix[STOP_TAG], tags[-1]]
        return score

    def _forward_alg(self, feats):
        # 通过前向算法递推计算
        init_alphas = torch.full((1, self.tagset_size), -10000.)
        # 初始化step=0，即Start位置的发射分数，Start_Tag取0，其他位置取-10000（意思就是开始位置只有可能是Start_tag）
        init_alphas[0][self.tag_to_ix[START_TAG]] = 0.

        # 将初始化Start位置为0的发射分数赋值给previous
        previous = init_alphas

        # 迭代整个句子
        for obs in feats:
            # 当前时间步的前向tensor
            alphas_t = []
            for next_tag in range(self.tagset_size):
                # 取出当前tag的发射分数，与之前时间的tag无关
                emit_score = obs[next_tag].view(1, -1).expand(1, self.tagset_size)
                # 取出当前tag与之前tag转移过来的转移分数
                trans_score = self.transitions[next_tag].view(1, -1)
                # 当前路径的分数：之前时间步分数+转移分数+发射分数
                next_tag_var = previous + trans_score + emit_score
                # 对当前分数取log_sum_exp
                alphas_t.append(log_sum_exp(next_tag_var).view(1))
            # 更新previous，递推计算下一个时间步
            previous = torch.cat(alphas_t).view(1, -1)
        # 考虑最终转移到STOP_TAG
        terminal_var = previous + self.transitions[self.tag_to_ix[STOP_TAG]]
        # 计算最终分数
        alpha = log_sum_exp(terminal_var)
        return alpha

    def _viterbi_decode(self, feats):
        backpointers = []  # 回溯指针

        # 初始化viterbi的previous变量
        init_vvars = torch.full((1, self.tagset_size), -10000.)
        init_vvars[0][self.tag_to_ix[START_TAG]] = 0

        previous = init_vvars
        for obs in feats:
            # 保存当前时间步的回溯指针，假设一个句子有11个单词，共有5个类别标签，bptrs_t的size为[11, 5]
            # 每个单词对应1个5维的索引值，其表示每个类别从上个单词哪个类别转移过来得分最高
            bptrs_t = []
            # 保存当前时间步的viterbi变量
            viterbivars_t = []

            for next_tag in range(self.tagset_size):
                # 维特比算法记录最优路径时只考虑上一步的分数以及上一步tag转移到当前tag的转移分数
                # 并不取决于当前tag的发射分数
                next_tag_var = previous + self.transitions[next_tag]
                # 获取最大分数的索引，这个最大分数是指从上个单词哪个类别转移到当前单词当前类别
                best_tag_id = argmax(next_tag_var)
                bptrs_t.append(best_tag_id)
                viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))
            # 更新previous，加上当前tag的发射分数obs
            previous = (torch.cat(viterbivars_t) + obs).view(1, -1)
            # 回溯指针记录当前时间步各个tag来源前一步的tag
            backpointers.append(bptrs_t)

        # 考虑转移到STOP_TAG的转移分数
        terminal_var = previous + self.transitions[self.tag_to_ix[STOP_TAG]]
        best_tag_id = argmax(terminal_var)
        path_score = terminal_var[0][best_tag_id]

        # 通过回溯指针解码出最优路径
        best_path = [best_tag_id]
        for bptrs_t in reversed(backpointers):
            best_tag_id = bptrs_t[best_tag_id]
            best_path.append(best_tag_id)
        # 去除start_tag
        start = best_path.pop()
        assert start == self.tag_to_ix[START_TAG]  # Sanity check
        best_path.reverse()
        return path_score, best_path

    def neg_log_likelihood(self, sentence, tags):
        # CRF损失函数有两部分组成，真实路径的分数和所有路径的总分数
        # 真实路径的分数应该是所有路径中分数最高的
        # log(真实路径的分数)/log(所有可能路径的分数)，越大越好，构造crf_loss函数取反 ，loss越小越好
        feats = self._get_lstm_features(sentence)
        forward_score = self._forward_alg(feats)
        gold_score = self._score_sentence(feats, tags)
        return forward_score - gold_score

    def forward(self, sentence):
        # 注意不要把这个forward与之前的forward_arg搞混了
        # 通过BiLSTM提取发射分数
        lstm_feats = self._get_lstm_features(sentence)

        # 根据发射分数以及转移分数，通过viterbi解码找到一条最优路径
        score, tag_seq = self._viterbi_decode(lstm_feats)
        return score, tag_seq


if __name__ == "__main__":
    START_TAG = "<START>"
    STOP_TAG = "<STOP>"
    EMBEDDING_DIM = 5
    HIDDEN_DIM = 4

    # Make up some training data
    training_data = [(
        "the wall street journal reported today that apple corporation made money".split(),
        "B I I I O O O B I O O".split()
    ), (
        "georgia tech is a university in georgia".split(),
        "B I O O O O B".split()
    )]

    word_to_ix = {}
    for sentence, tags in training_data:
        for word in sentence:
            if word not in word_to_ix:
                word_to_ix[word] = len(word_to_ix)

    tag_to_ix = {"B": 0, "I": 1, "O": 2, START_TAG: 3, STOP_TAG: 4}

    model = BiLSTM_CRF(len(word_to_ix), tag_to_ix, EMBEDDING_DIM, HIDDEN_DIM)
    optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-4)

    # 训练前检查模型预测结果
    with torch.no_grad():
        precheck_sent = prepare_sequence(training_data[0][0], word_to_ix)
        precheck_tags = torch.tensor([tag_to_ix[t] for t in training_data[0][1]], dtype=torch.long)
        print(f"训练前网络得到的标签为：{model(precheck_sent)}")
        print(f"正确的标签为：{precheck_tags}")

    # Make sure prepare_sequence from earlier in the LSTM section is loaded
    for epoch in range(300):  # again, normally you would NOT do 300 epochs, it is toy data
        for sentence, tags in training_data:
            # 第一步，pytorch梯度积累，需要先清零梯度
            model.zero_grad()

            # 第二步，将输出转换为tensor
            sentence_in = prepare_sequence(sentence, word_to_ix)
            targets = torch.tensor([tag_to_ix[t] for t in tags], dtype=torch.long)

            # 第三步，进行前向计算，得到crf loss
            loss = model.neg_log_likelihood(sentence_in, targets)

            # 第四步，计算loss,梯度，通过optimizer更新参数
            loss.backward()
            optimizer.step()

    # 训练结束查看模型预测结果，对比观察模型是否学到东西
    with torch.no_grad():
        precheck_sent = prepare_sequence(training_data[0][0], word_to_ix)
        print(f"训练后网络得到的标签为：{model(precheck_sent)}")
    # We got it!

训练前网络得到的标签为：(tensor(2.6907), [1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1])
正确的标签为：tensor([0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2])
训练后网络得到的标签为：(tensor(20.4906), [0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2])

使用pytorch-crf包来增加CRF层

上面的BiLSTM-CRF的实现是Pytorch官网给出的一个实现方式，对于我们理解BiLSTM-CRF的原理是非常有帮助的，实际上当我们理解了原理之后还可以使用pytorch内置的包来增加CRF层，可以进一步精简代码

首选包安装：pip install pytorch-crf

如果安装后使用报错可以尝试卸载重新安装，或者使用国内镜像安装，我遇到过安装后使用报错，但是卸载重新安装就正常了的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
# coding=utf-8
import torch
import torch.nn as nn
from torchcrf import CRF
import torch.nn.functional as F
import torch.optim as optim


class BiLSTM_CRF(nn.Module):
    def __init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_size, num_layers, use_crf=True, seq_length=256):
        super(BiLSTM_CRF, self).__init__()
        self.embedding_dim = embedding_dim  # 词向量维度（长度），即用多少维度向量表示一个词
        self.hidden_size = hidden_size  # 单向lstm的hidden_size
        self.vocab_size = vocab_size  # 词表大小
        self.tag_to_ix = tag_to_ix    # 标签序号的映射字典
        self.tagset_size = len(tag_to_ix)  # 标签数量/类别数
        self.num_layers = num_layers
        self.use_crf = use_crf
        self.seq_length = seq_length  # 句子最大长度，超过截断，小于填充,会将所有输入神经网络的句子向量统一为该长度

        # 词嵌入层，size为(词表大小, 词向量维度)
        self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
        # 双向lstm
        self.lstm = nn.LSTM(embedding_dim, hidden_size, bidirectional=True, num_layers=num_layers, batch_first=True)
        # 将BiLSTM提取的特征向量映射到特征空间，即经过全连接得到发射分数
        self.hidden2tag = nn.Linear(hidden_size*2, self.tagset_size)
        if use_crf:
            # crf层，可以使用pytorch的crf包
            self.crf = CRF(self.tagset_size, batch_first=True)

    def forward(self, sentence, seg, targets=None):
        """
        NER model的前向传播过程
        :param sentence: 传入句子，size(batch_size, seq_length)
        :param seg:      =1的位置表示是句子的有效部分         size(batch_size, seq_length)
        :param targets:  标签，计算损失时需要, size(batch_size, seq_length)
        :return:
        """
        # 得到词向量
        embeddings = self.word_embeds(sentence)
        # 由于lstm层的输入必须是三维的, 当传入的sentence为单个句子且只有一维时，需要对词向量增加维度.view(len(sentence), 1, -1)
        # lstm层返回输出和隐状态，输出size为(batch_size, seq_length, hidden_size*2)
        # 隐状态是有两个元素的tuple(因为双向),每个元素size为(2, seq_length, hidden_size)
        lstm_out, hidden_state = self.lstm(embeddings)
        # 经过全连接层得到发射分数
        features = self.hidden2tag(lstm_out)
        if self.use_crf:
            tgt_mask = seg.type(torch.uint8)
            pred = self.crf.decode(features, mask=tgt_mask)
            for j in range(len(pred)):
                # 以STOP_TAG的id填充至seq_length长度
                while len(pred[j]) < self.seq_length:
                    pred[j].append(self.tagset_size-1)
            # 从(batch_size, seq_length)转成(batch_size*seq_length)一维
            pred = torch.tensor(pred).contiguous().view(-1)
            # 传入targets时，计算损失
            if targets is not None:
                loss = -self.crf(F.log_softmax(features, 2), targets, mask=tgt_mask, reduction='mean')
                return loss, pred
            else:
                return None, pred
        else:
            tgt_mask = seg.contiguous().view(-1).float()
            # 变成两维，(batch_size*seq_length, tagset_size)
            features = features.contiguous().view(-1, self.tagset_size)
            # 如果没有CRF层，就直接取值最大的类别(argmax与torch.max的区别是只返回索引)
            pred = features.argmax(dim=-1)
            if targets is not None:
                targets = targets.contiguous().view(-1, 1)  # 转变成(batch_size*seq_length, 1)
                # 先zero初始化一个(batch_size*seq_length, tagset_size)的张量，然后根据标签转成One-hot编码
                one_hot = (torch.zeros(targets.size(0), self.tagset_size)
                           .to(torch.device(targets.device)).scatter_(1, targets, 1.0))
                # 先针对features的最后一维进行Log_softmax，再乘以One-hot向量（这里为什么不直接使用多分类交叉熵损失函数？）
                numerator = -torch.sum(nn.LogSoftmax(dim=-1)(features) * one_hot, 1)
                numerator = torch.sum(tgt_mask * numerator)
                denominator = torch.sum(tgt_mask) + 1e-6
                loss = numerator / denominator
                return loss, pred
            else:
                return None, pred


def prepare_sequence(seq, to_ix):
    """
    获取传入文本在词典中的序号
    :param seq: 传入分割好的文本，以列表形式
    :param to_ix: 单词/词语 到 序号的映射字典
    :return:
    """
    idxs = [to_ix[w] for w in seq]
    return torch.tensor(idxs, dtype=torch.long)


if __name__ == "__main__":
    START_TAG = "<START>"
    STOP_TAG = "<STOP>"
    EMBEDDING_DIM = 6
    HIDDEN_DIM = 5
    num_layers = 1

    # Make up some training data
    training_data = [(
        "the wall street journal reported today that apple corporation made money".split(),
        "B I I I O O O B I O O".split()
    ), (
        "georgia tech is a university in georgia".split(),
        "B I O O O O B".split()
    )]

    word_to_ix = {}
    for sentence, tags in training_data:
        for word in sentence:
            if word not in word_to_ix:
                word_to_ix[word] = len(word_to_ix)

    tag_to_ix = {"B": 0, "I": 1, "O": 2, START_TAG: 3, STOP_TAG: 4}

    model = BiLSTM_CRF(len(word_to_ix), tag_to_ix, EMBEDDING_DIM, HIDDEN_DIM, num_layers, use_crf=False)
    optimizer = optim.SGD(model.parameters(), lr=0.1, weight_decay=1e-4)

    # 训练前检查模型预测结果
    with torch.no_grad():
        # 此demo里并未对训练数据统一补充为seq_length的长度，那么就不能一个批次同时输入多条句子
        sentence1 = prepare_sequence(training_data[0][0], word_to_ix)
        sentence1_tags = torch.tensor([tag_to_ix[t] for t in training_data[0][1]], dtype=torch.long)
        sentence2 = prepare_sequence(training_data[1][0], word_to_ix)
        sentence2_tags = torch.tensor([tag_to_ix[t] for t in training_data[1][1]], dtype=torch.long)
        # batch_sentence = torch.tensor([sentence1, sentence2])
        # batch_tags = torch.tensor([sentence1_tags, sentence2_tags])
        seg = torch.tensor([1] * len(sentence1))
        sentence1 = sentence1.view(1, -1)  # 如果sentence是单个句子，可以在第0维增加一维
        seg = seg.view(1, -1)
        _, batch_pred1 = model(sentence1, seg)  # 返回损失和预测
        print(f"句子1训练前网络得到的标签为：{batch_pred1[:len(sentence1[0])]}")  # 这里一个batch就一个元素，所以直接取0
        print(f"句子1正确的标签为：{sentence1_tags}")

        seg = torch.tensor([1] * len(sentence2)).view(1, -1)
        sentence2 = sentence2.view(1, -1)
        _, batch_pred2 = model(sentence2, seg)  # 返回损失和预测
        print(f"句子2训练前网络得到的标签为：{batch_pred2[:len(sentence2[0])]}")  # 这里一个batch就一个元素，所以直接取0
        print(f"句子2正确的标签为：{sentence2_tags}")

    # Make sure prepare_sequence from earlier in the LSTM section is loaded
    for epoch in range(300):  # again, normally you would NOT do 300 epochs, it is toy data
        for sentence, tags in training_data:
            # 第一步，pytorch梯度积累，需要先清零梯度
            model.zero_grad()

            # 第二步，将输出转换为tensor
            sentence_in = prepare_sequence(sentence, word_to_ix)
            seg = torch.tensor([1] * len(sentence_in))
            sentence_in = sentence_in.view(1, -1)
            seg = seg.view(1, -1)
            targets = torch.tensor([tag_to_ix[t] for t in tags], dtype=torch.long)
            # target也要增加一维
            targets = targets.view(1, -1)
            # 第三步，进行前向计算，得到crf loss，当传入target时会自动计算loss
            loss, _ = model(sentence_in, seg, targets)

            # 第四步，计算loss,梯度，通过optimizer更新参数
            loss.backward()
            optimizer.step()

    # 训练结束查看模型预测结果，对比观察模型是否学到东西
    with torch.no_grad():
        seg = torch.tensor([1]*len(sentence1[0])).view(1, -1)
        _, preds1 = model(sentence1, seg)
        print(f"句子1训练后网络得到的标签为：{preds1[:len(sentence1[0])]}")
        seg = torch.tensor([1] * len(sentence2[0])).view(1, -1)
        _, preds2 = model(sentence2, seg)
        print(f"句子2训练后网络得到的标签为：{preds2[:len(sentence2[0])]}")
    # We got it!

句子1训练前网络得到的标签为：tensor([4, 4, 3, 4, 0, 4, 4, 0, 3, 3, 4])
句子1正确的标签为：tensor([0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2])
句子2训练前网络得到的标签为：tensor([4, 4, 4, 4, 4, 0, 4])
句子2正确的标签为：tensor([0, 1, 2, 2, 2, 2, 0])
句子1训练后网络得到的标签为：tensor([0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2])
句子2训练后网络得到的标签为：tensor([0, 1, 2, 2, 2, 2, 0])

这里在模型的forward前向计算部分，其实是我从UER-py的框架代码里借鉴的，重点来看一下损失计算这部分

1
loss = -self.crf(F.log_softmax(features, 2), targets, mask=tgt_mask, reduction='mean')

先打印一下features和F.log_softmax(features, dim=2)，看一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
tensor([[[ 0.2056, -0.1778,  0.3660,  0.1293, -0.2844],
         [ 0.1895, -0.1792,  0.3430,  0.1270, -0.2139],
         [ 0.1952, -0.1807,  0.3810,  0.0988, -0.3275],
         [ 0.2284, -0.2302,  0.3037,  0.1401, -0.2611],
         [ 0.1485, -0.1867,  0.3787,  0.1309, -0.3057],
         [ 0.1784, -0.1761,  0.3400,  0.1349, -0.2641],
         [ 0.2223, -0.2179,  0.3341,  0.1052, -0.3031],
         [ 0.1790, -0.2088,  0.3403,  0.1347, -0.2798],
         [ 0.1946, -0.2041,  0.3254,  0.1393, -0.2897],
         [ 0.2030, -0.1748,  0.3544,  0.1387, -0.2588],
         [ 0.1980, -0.2170,  0.2821,  0.1241, -0.2678]]],
       grad_fn=<AddBackward0>)
tensor([[[-1.4804, -1.8638, -1.3200, -1.5567, -1.9704],
         [-1.4962, -1.8650, -1.3428, -1.5588, -1.8996],
         [-1.4798, -1.8557, -1.2939, -1.5762, -2.0025],
         [-1.4442, -1.9029, -1.3690, -1.5326, -1.9338],
         [-1.5242, -1.8595, -1.2940, -1.5418, -1.9784],
         [-1.4989, -1.8534, -1.3373, -1.5424, -1.9414],
         [-1.4453, -1.8855, -1.3335, -1.5623, -1.9707],
         [-1.4912, -1.8790, -1.3298, -1.5355, -1.9500],
         [-1.4755, -1.8742, -1.3447, -1.5308, -1.9598],
         [-1.4854, -1.8632, -1.3340, -1.5497, -1.9472],
         [-1.4597, -1.8747, -1.3755, -1.5335, -1.9255]]],
       grad_fn=<LogSoftmaxBackward>)

features这里是一个(1, 11, 5)的张量，第0维是batch_size大小，第1维是句子长度，第2维是词向量维度。log_softmax是先进行softmax运算再取log，dim=2表示在第2维上进行log_softmax运算。

以[ 0.2056, -0.1778, 0.3660, 0.1293, -0.2844]举例，进行softmax运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import math


v = [ 0.2056, -0.1778,  0.3660,  0.1293, -0.2844]
sum = sum([math.exp(i) for i in v])

# 等价于F.softmax(torch.tensor(v, dtype=torch.float))
s = [round(math.exp(i)/sum, 4) for i in v]
print(s)
[0.2275, 0.1551, 0.2671, 0.2108, 0.1394]

# 对s[0]取log
print(round(math.log(s[0]), 4))
-1.4806

这里targets和tgt_mask都是(batch_size, seq_length)的size，target就是对应的标签，比如在NER任务中，一个单词对应的是BIO哪个标签，tgt_mask则用来标记一个句子的有效部分，比如一条句子的长度为100个字，在传入模型之前需要统一成长度为300的张量，那么后两百个元素的值都是填充的句子结束标记，这部分在训练时是不需要计算损失的，预测的时候也是不需要关注这部分的值，这里就是通过mask参数来区分句子的有效部分；

另外如果batch_first=False，则mask的size应该为(seq_length, batch_size)。

还可以看到，我在这里加了use-crf参数，即可以通过该参数来指定是否增加CRF层，当没有CRF层时，取预测结果时就是直接对features中每个单词特征的最大值，损失函数也是采用了另外的计算方式（这里的计算方式时借鉴了UER-py中的NER模型，原理思想没怎么搞明白，我想的是应该是可以直接使用多分类交叉熵损失函数的，后面还会介绍使用多分类交叉熵损失函数的版本）。

但是注意，这里不使用CRF层训练，300轮后最后无法正确预测这两个样本的标签，但是通过将学习率由0.01增大至0.1，在300轮后则可以正确预测，推测是学习率太小，300轮并未得到充分学习。之后我将学习率设为0.01。然后将训练轮次增加至1000，顺利得到了正确的预测结果。

BiLSTM-CRF的实现V3版本

在这一版本的实现中，我进行了如下的优化：

  1. 变量的命名更易于理解；
  2. 在word_embedding后面增加LayerNorm层；
  3. 增加dropout层；
  4. 在训练demo中，采用了更贴近实际情况的方法，即将句子统一成seq_length长度的张量并按照批次传入模型；
  5. 无crf层的损失函数实现，直接使用nn.CrossEntropyLoss，但是依然要考虑到targets_mask的问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
# coding=utf-8
"""
与bi-lstm-crf-v2相比，修改了无crf层时的损失函数，直接使用nn.CrossEntropyLoss
"""
import torch
import torch.nn as nn
from torchcrf import CRF
import torch.nn.functional as F
import torch.optim as optim


class BiLSTM_CRF(nn.Module):
    def __init__(self, vocab_size, label_to_id, embedding_dim, hidden_size, num_layers,
                 use_crf=True, seq_length=256, dropout=0.0):
        super(BiLSTM_CRF, self).__init__()
        self.embedding_dim = embedding_dim  # 词向量维度（长度），即用多少维度向量表示一个词
        self.hidden_size = hidden_size  # 单向lstm的hidden_size
        self.vocab_size = vocab_size  # 词表大小
        self.label_to_id = label_to_id    # 标签序号的映射字典
        self.label_nums = len(label_to_id)  # 标签数量/类别数
        self.num_layers = num_layers  # LSTM层数
        self.use_crf = use_crf  # 是否使用CRF层
        self.seq_length = seq_length  # 句子最大长度，超过截断，小于填充,会将所有输入神经网络的句子向量统一为该长度

        # 词嵌入层，size为(词表大小, 词向量维度)
        self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
        # LayerNorm层
        self.layer_norm = nn.LayerNorm(embedding_dim)
        # dropout层
        self.dropout = nn.Dropout(dropout)
        # 双向lstm
        self.lstm = nn.LSTM(embedding_dim, hidden_size, bidirectional=True, num_layers=num_layers, dropout=dropout, batch_first=True)
        # 将BiLSTM提取的特征向量映射到特征空间，即经过全连接得到发射分数
        self.hidden2tag = nn.Linear(hidden_size*2, self.label_nums)
        if use_crf:
            # crf层，可以使用pytorch的crf包
            self.crf = CRF(self.label_nums, batch_first=True)

    def forward(self, sentence, targets_mask, targets=None):
        """
        NER model的前向传播过程
        :param sentence: 传入句子，size(batch_size, seq_length)
        :param targets_mask: 标签是否有效的标志，=1的部分是句子的有效部分，size(batch_size, seq_length)
        :param targets:  标签，计算损失时需要, size(batch_size, seq_length)
        :return:
        """
        # 得到词向量
        embeddings = self.word_embeds(sentence)
        embeddings = self.dropout(self.layer_norm(embeddings))
        # 由于lstm层的输入必须是三维的, 当传入的sentence为单个句子且只有一维时，需要对词向量增加维度.view(len(sentence), 1, -1)
        # lstm层返回输出和隐状态，输出size为(batch_size, seq_length, hidden_size*2)
        # 隐状态是有两个元素的tuple(因为双向),每个元素size为(2, seq_length, hidden_size)
        lstm_out, hidden_state = self.lstm(embeddings)
        lstm_out = self.dropout(lstm_out)
        # 经过全连接层得到发射分数,size:(batch_size, seq_length, label_nums)
        features = self.hidden2tag(lstm_out)
        if self.use_crf:
            targets_mask = targets_mask.type(torch.uint8)
            pred = self.crf.decode(features, mask=targets_mask)
            for j in range(len(pred)):
                # 以STOP_TAG的id填充至seq_length长度
                while len(pred[j]) < self.seq_length:
                    pred[j].append(self.label_nums-1)
            # 从(batch_size, seq_length)转成(batch_size*seq_length)一维
            pred = torch.tensor(pred).contiguous().view(-1)
            # 传入targets时，计算损失
            if targets is not None:
                # targets_mask=1的部分计算损失
                loss = -self.crf(F.log_softmax(features, 2), targets, mask=targets_mask, reduction='mean')
                return loss, pred
            else:
                return None, pred
        else:
            if targets is not None:
                total_loss = 0.0
                batch_size = features.size()[0]
                for i in range(batch_size):
                    length = torch.sum(targets_mask[i])  # 求出来的值就是1的数量，也就表示这个句子的长度
                    single_feature = features[i][:length]  # 只计算句子有效部分的损失
                    single_target = targets[i][:length]
                    # 使用mean和sum所需的学习率可能有不同的要求
                    loss_f = nn.CrossEntropyLoss(reduction='mean')
                    loss = loss_f(single_feature, single_target)
                    total_loss += loss
                batch_loss = total_loss / batch_size
                # 为了统一返回的pred的size
                features = features.contiguous().view(-1, self.label_nums)
                pred = features.argmax(dim=-1)
                return batch_loss, pred
            else:
                features = features.contiguous().view(-1, self.label_nums)
                pred = features.argmax(dim=-1)
                return None, pred

def prepare_data(data, to_ix, seq_length, label_to_id):
    """
    获取传入文本在词典中的序号
    :param data: 训练数据，tuple形式，第一个元素是分割好的文本，以列表形式；第二个元素是标签，以列表形式
    :param to_ix: 单词/词语 到 序号的映射字典
    :param seq_length: 需要统一的句子长度
    :param label_to_id: 标签序号的映射字典
    :return:
    """
    seq = data[0]
    labels = data[1]
    text_ids = [to_ix[w] for w in seq]
    targets = [label_to_id[t] for t in labels]
    targets_mask = [1] * len(text_ids)
    if len(text_ids) > seq_length:
        text_ids = text_ids[:seq_length]
        targets = targets[:seq_length]
        targets_mask = targets_mask[:seq_length]
    while len(text_ids) < seq_length:
        text_ids.append(to_ix["[PAD]"])
        targets.append(label_to_id[STOP_TAG])
        targets_mask.append(0)
    return text_ids, targets_mask, targets


if __name__ == "__main__":
    START_TAG = "<START>"
    STOP_TAG = "<STOP>"
    EMBEDDING_DIM = 6
    HIDDEN_DIM = 5
    num_layers = 1
    seq_length = 20  # 将句子统一成20的长度

    # Make up some training data
    training_data = [(
        "the wall street journal reported today that apple corporation made money".split(),
        "B I I I O O O B I O O".split()
    ), (
        "georgia tech is a university in georgia".split(),
        "B I O O O O B".split()
    )]

    word_to_id = {}  # 词典
    for sentence, tags in training_data:
        for word in sentence:
            if word not in word_to_id:
                word_to_id[word] = len(word_to_id)
    word_to_id["[PAD]"] = len(word_to_id)

    label_to_id = {"B": 0, "I": 1, "O": 2, START_TAG: 3, STOP_TAG: 4}

    model = BiLSTM_CRF(len(word_to_id), label_to_id, EMBEDDING_DIM, HIDDEN_DIM, num_layers,
                       use_crf=False, seq_length=seq_length)
    optimizer = optim.SGD(model.parameters(), lr=0.1, weight_decay=1e-4)

    # 训练前检查模型预测结果
    with torch.no_grad():
        sentence0_length = len(training_data[0][0])
        sentence1_length = len(training_data[1][0])
        sentence0, targets_mask_0, targets_0 = prepare_data(training_data[0], word_to_id, seq_length, label_to_id)
        sentence1, targets_mask_1, targets_1 = prepare_data(training_data[1], word_to_id, seq_length, label_to_id)
        batch_sentence_0 = torch.tensor([sentence0, sentence1])
        # batch_targets_0 = torch.tensor([targets_0])
        batch_targets_mask_0 = torch.tensor([targets_mask_0, targets_mask_1])
        _, batch_pred0 = model(batch_sentence_0, batch_targets_mask_0)  # 返回损失和预测
        print(f"句子1训练前网络得到的标签为：{batch_pred0[:sentence0_length]}")
        print(f"句子2训练前网络得到的标签为：{batch_pred0[seq_length:seq_length+sentence1_length]}")
        print(f"句子1正确的标签为：{targets_0[:sentence0_length]}")
        print(f"句子2正确的标签为：{targets_1[:sentence1_length]}")

    # Make sure prepare_sequence from earlier in the LSTM section is loaded
    for epoch in range(300):  # again, normally you would NOT do 300 epochs, it is toy data
        # 第一步，pytorch梯度积累，需要先清零梯度
        model.zero_grad()

        sentence0, targets_mask_0, targets_0 = prepare_data(training_data[0], word_to_id, seq_length, label_to_id)
        sentence1, targets_mask_1, targets_1 = prepare_data(training_data[1], word_to_id, seq_length, label_to_id)
        batch_sentence = torch.tensor([sentence0, sentence1])
        batch_targets = torch.tensor([targets_0, targets_1])
        batch_targets_mask = torch.tensor([targets_mask_0, targets_mask_1])
        # 第三步，进行前向计算，得到crf loss，当传入target时会自动计算loss
        loss, _ = model(batch_sentence, batch_targets_mask, batch_targets)

        # 第四步，计算loss,梯度，通过optimizer更新参数
        loss.backward()
        optimizer.step()

    # 训练结束查看模型预测结果，对比观察模型是否学到东西
    with torch.no_grad():
        _, batch_pred0 = model(batch_sentence_0, batch_targets_mask_0)  # 返回损失和预测
        print(f"句子1训练后网络得到的标签为：{batch_pred0[:sentence0_length]}")
        print(f"句子2训练后网络得到的标签为：{batch_pred0[seq_length:seq_length+sentence1_length]}")
    # We got it!

    
句子1训练前网络得到的标签为：tensor([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
句子2训练前网络得到的标签为：tensor([2, 2, 2, 2, 2, 2, 2])
句子1正确的标签为：[0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2]
句子2正确的标签为：[0, 1, 2, 2, 2, 2, 0]
句子1训练后网络得到的标签为：tensor([0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2])
句子2训练后网络得到的标签为：tensor([0, 1, 2, 2, 2, 2, 0])

与V2版本相比，使用CRF层时模型学习的更快更好；不使用CRF层时，对超参数的设置要求更高了，比如损失函数的reduction='sum'时，在学习率0.01和300轮的训练后，模型可以正确预测出这两个样本的标签，而在设置reduction='mean'时，在学习率0.01的情况下，则需要更多的轮次才能正确预测，如果将学习率设置为0.1则可以更快地学习。

关于LSTM的Hidden初始化

通过v1版本的代码可以看到，官方实现时是给lstm网络的输入参数中显示地传入了初始化值，而我们在V2和V3版本中则省去了这一操作，下面就来详细解释一下这一区别是否重要，首先我们需要了解torch.nn.LSTM的主要参数及其含义：

  1. input_size（必需参数）：输入数据的特征维度大小。这是输入序列的特征向量的维度。

  2. hidden_size（必需参数）：LSTM 单元的隐藏状态的维度大小。这决定了 LSTM 层的输出和内部隐藏状态的维度。

  3. num_layers（可选参数，默认为 1）：LSTM 层的堆叠层数。你可以将多个 LSTM 层叠加在一起，以增加模型的容量和表示能力。

  4. bias（可选参数，默认为 True）：一个布尔值，确定是否在 LSTM 单元中包含偏置项。

  5. batch_first（可选参数，默认为 False）：一个布尔值，指定输入数据的形状。如果设置为 True，输入数据的形状应为 (batch_size, sequence_length, input_size)，否则为 (sequence_length, batch_size, input_size)。

  6. dropout（可选参数，默认为 0.0）：应用于除最后一层外的每个 LSTM 层的丢弃率。这有助于防止过拟合。

  7. bidirectional（可选参数，默认为 False）：一个布尔值，指定是否使用双向 LSTM。如果设置为 True，LSTM 将具有前向和后向的隐藏状态，以更好地捕捉序列的上下文信息。

  8. device（可选参数）：指定要在哪个设备上创建 LSTM 层，例如 CPU 或 GPU。

  9. dtype（可选参数）：指定数据类型，例如 torch.float32 或 torch.float64。

  10. return_sequences（可选参数，默认为 False）：一个布尔值，指定是否返回每个时间步的输出序列。如果设置为 True，则返回完整的输出序列；否则，只返回最后一个时间步的输出。

通过以上参数来定义一个LSTM网络，在前向传播时需要传入输入数据进行计算

torch.nn.LSTM 层的输入通常是一个包含两个元素的元组 (input, (h_0, c_0))，调用方法为：

output, (h_n, c_n) = torch.nn.LSTM(input, (h_0,c_0))

其中：

(1) input 通常是一个三维张量，具体形状取决于是否设置了 batch_first 参数。输入张量包括以下维度：

  1. 批量维度（Batch Dimension）：这是数据中的样本数量。如果 batch_first 设置为 True，那么批量维度将是第一个维度；否则，批量维度将是第二个维度。

  2. 序列长度维度（Sequence Length Dimension）：这是时间步的数量，也是序列的长度。它是输入序列中数据点的数量。

  3. 特征维度（Feature Dimension）：这是输入数据点的特征数量。它表示每个时间步的输入特征向量 xt 的维度。

根据上述描述，以下是两种常见的输入形状：

  • 如果 batch_first 为 True：

    • 输入张量的形状为 (batch_size, sequence_length, input_size)。
    • batch_size 是批量大小，表示同时处理的样本数量。
    • sequence_length 是序列的长度，即时间步的数量。
    • input_size 是输入特征向量的维度。

  • 如果 batch_first 为 False：

    • 输入张量的形状为 (sequence_length, batch_size, input_size)。
    • sequence_length 是序列的长度，即时间步的数量。
    • batch_size 是批量大小，表示同时处理的样本数量。

    • input_size 是输入特征向量的维度。

      要注意的是，这只是输入的形状，LSTM 层的参数（例如 input_size 和 hidden_size）必须与输入形状相匹配。根据你的具体任务和数据，你需要将输入数据整理成适当形状的张量，然后将其传递给 torch.nn.LSTM 层以进行前向传播。

(2) (h_0, c_0)：是包含初始隐藏状态和初始细胞状态的元组。

  • h_0：是初始隐藏状态，其形状为 (num_layers * num_directions, batch_size, hidden_size)。num_layers 是 LSTM 层的堆叠层数，num_directions 是 1 或 2，取决于是否使用双向 LSTM。
  • c_0：是初始细胞状态，其形状也为 `(num_layers * num_directions

上面关于h_0、c_0的初始化size描述的非常清楚，如果你在网络计算时并未传入这两个参数，其实通过查看源代码会发现在lstm的内部同样会初始化这两个参数，区别是使用的是torch.zero，即都初始化为0，而v1版本中则是使用的torch.randn，所以说具体如何初始化效果会更好还是需要自行测试。

参考博文链接：https://blog.csdn.net/m0_48241022/article/details/132775071

应用到命名实体识别

上面对于BiLSTM模型的原理和实现我们已经基本掌握，接下来就是应用到命名实体识别的实际任务中。这部分内容会在后续的github项目中展示，其实整体是借鉴的UER-py这个项目，只不过改写了部分代码。

这里我仅将我的实验结果进行展示，对于模型的评估一共有两个指标，一种是根据实体数量评估，一种是根据单条数据评估（单条数据可能包含多个实体）。
实验数据一：
embedding_size=256, hidden_size=512(单向), use_crf=True, layer_nums=2
按照实体数量评估：F1=99.0%，按照单条数据评估：F1=95.7%
2600条测试数据，大约有26000个实体，1%的实体预测不准确，大概也有260个实体，最多可能导致260条数据提取不准确。
参数量：14,963,378，权重大小：57MB

实验数据二:
embedding_size=256, hidden_size=512(单向), user_crf=False, layer_nums=2
按照实体数量评估：F1=95.3%，按照单条数据评估：F1=78.4%
2600条测试数据，大约有26000个实体，4.7%的实体预测不准确，大概有1222个实体，最多可能导致1222条数据提取不准确。
可以看到效果相比使用CRF确实下降很多。
参数量：14,955,098，权重大小：57MB，与使用CRF几乎相同

实验数据三：
embedding_size=512, hidden_size=768(单向), use_crf=True, layer_nums=2
按照实体数量评估：F1=99.4%，按照单条数据评估：96.5%
2600条测试数据，大约有26000个实体，0.6%的实体预测不准确，大概也有156个实体，最多可能导致156条数据提取不准确。
参数量：33,009,842，权重大小：125MB

实验数据四:
embedding_size=512, hidden_size=768(单向), use_crf=False, layer_nums=2
按照实体数量评估：F1=96.8%，按照单条数据评估：F1=82.3%
2600条测试数据，大约有26000个实体，3.2%的实体预测不准确，大概有832个实体，最多可能导致832条数据提取不准确。
参数量：33,001,562，权重大小：125MB，与使用CRF几乎相同

实验数据五：
embedding_size=384, hidden_size=768(单向), use_crf=True, layer_nums=2
参数量：29,518,770，权重大小：112MB
按照实体数量评估：F1=99.4%，按照单条数据评估：96.9%
相比embedding_size=512，参数量略有减少，但是实际效果一致，甚至在以单条数据评估的基础上，取得了0.4%的提升。
batch_size=16可以再试一下

实验数据六：
embedding_size=256, hidden_size=512(单向), user_crf=True, layer_nums=3
参数量：21,263,026，权重大小：81MB
按照实体数量评估：F1=99.4%，按照单条数据评估：96.7%
单条数据预测速度：0.024s

后面更多的对比实验我以表格的形式展示更方便查看，就不再文字罗列，注意以下训练数据采用的优化器统一为SGD、学习率统一为0.001。

num_layers embedding_dim hidden_size use_crf 参数量 权重大小/MB F1 F2
2 256 512 False 14,955,098 57MB 95.3% 78.4%
2 256 512 True 14,963,378 52MB 99.0% 95.7%
3 256 512 True 21,263,026 81MB 99.4% 96.7%
2 384 768 True 29,518,770 112MB 99.4% 96.7%
3 384 768 True 43,686,834 166MB 99.3% 96.1%
2 512 768 False 33,001,562 125MB 96.8% 82.3%
2 512 768 True 33,009,842 125MB 99.4% 96.5%
2 512 1024 True 48,792,754 186MB 99.4% 96.7%
2(use_pre) 768 768 True 39,991,986 152MB 99.3% 96.1%
2 768 768 True 39,991,986 152MB 99.3% 96.4%
2(use_pre) 384 768 True 23,311,794 89MB 99.4% 96.7%

关于以上实验得到的结论：

  1. 根据实验一、二和实验三、四两组实验对比显示，使用CRF层可以得到大幅度的效果提升，并且参数量几乎不变，但是使用CRF的训练速度整体要比不使用CRF训练速度慢3~5倍，embedding_size=512,hidden_size=768的配置下，不使用CRF训练100轮大约需要23小时（单个2080Ti）；
  2. 在一定范围内，增加embedding_dim、hidden_size和layers可以提高模型精度，但是代价是训练和预测速度的下降；embedding_size=512,hidden_size=768的配置下其平均单条数据的预测速度为：
    use_crf=False, 0.011s；use_crf=True, 0.025s；
  3. 当模型增大到一定程度之后，实际效果反而会下降，例如第4、5行的对比；
  4. 第9行特别注释的use_pre是使用的bert的预训练embedding，注意是仅使用embedding层，实际验证效果并不明显；
  5. 最后一行使用word2vec按照单个字符分割训练了一个词向量，因为词表大小变小了，所以embedding层的参数量减少了很多，最终模型大小也降低了。

这个项目其实还有一些待尝试的方法，例如采用分词的方式去训练词向量，然后输入到NER模型中训练，不过选取哪一种分词库效果更好是需要去对比的；此外，可能还需要根据业务特点，自己去建立一个业务词典，保证这些词不会被分词工具给切割；以及是否可以提出针对此业务的更好地分词方法也是一个可以深入研究的点。

下一个项目我会利用tranformer encoder作为NER的encoder来进一步实验。

补充一些实验数据

使用上述训练得到的模型在真实数据集上做测试时，发现一些抽取异常的问题（并不是因为自动生成数据的方法有问题，只是抽取有问题的情形并不包含在生成数据的模板内，即模型未见过此类数据，也可以理解为模型泛化能力还有所欠缺）。针对抽取异常的数据进行人工修正后作为训练数据参与训练，包括566条训练数据和59条测试数据。
合并到之前的训练集后重新训练，下面依然设置了两组对照实验：

使用BERT的词表且未对词向量进行训练：num_layers=2，embedding_dim=384,hidden_size=768，F1值为98.8%，F2值为93.6%（可以看到相比原来准确率有所下降，原因尚不清楚）。
如果单独评测上面标注的59条测试数据，其F1值为94.7%，F2值为48/59=81.4%

使用word2vec训练词向量并生成词表，num_layers=2，embedding_dim=384,hidden_size=768，F1值为99.3%，F2值为96.2%。

对59条标注的测试数据的评测结果为:F1=96.4%，F2值为50/59=84.7%。

现在可以看到通过word2vec学习词向量对准确率有明显提升，是否可以考虑：

  1. 扩充词向量学习的数据集；
  2. 使用BERT微调获取词向量，后续可能需要一定的放缩才能直接用；
  3. 使用GPT微调获取词向量。

作为消融实验：可以通过仅训练566条数据，对59条测试数据准确率来判断生成的数据是否对模型学习有积极效果。