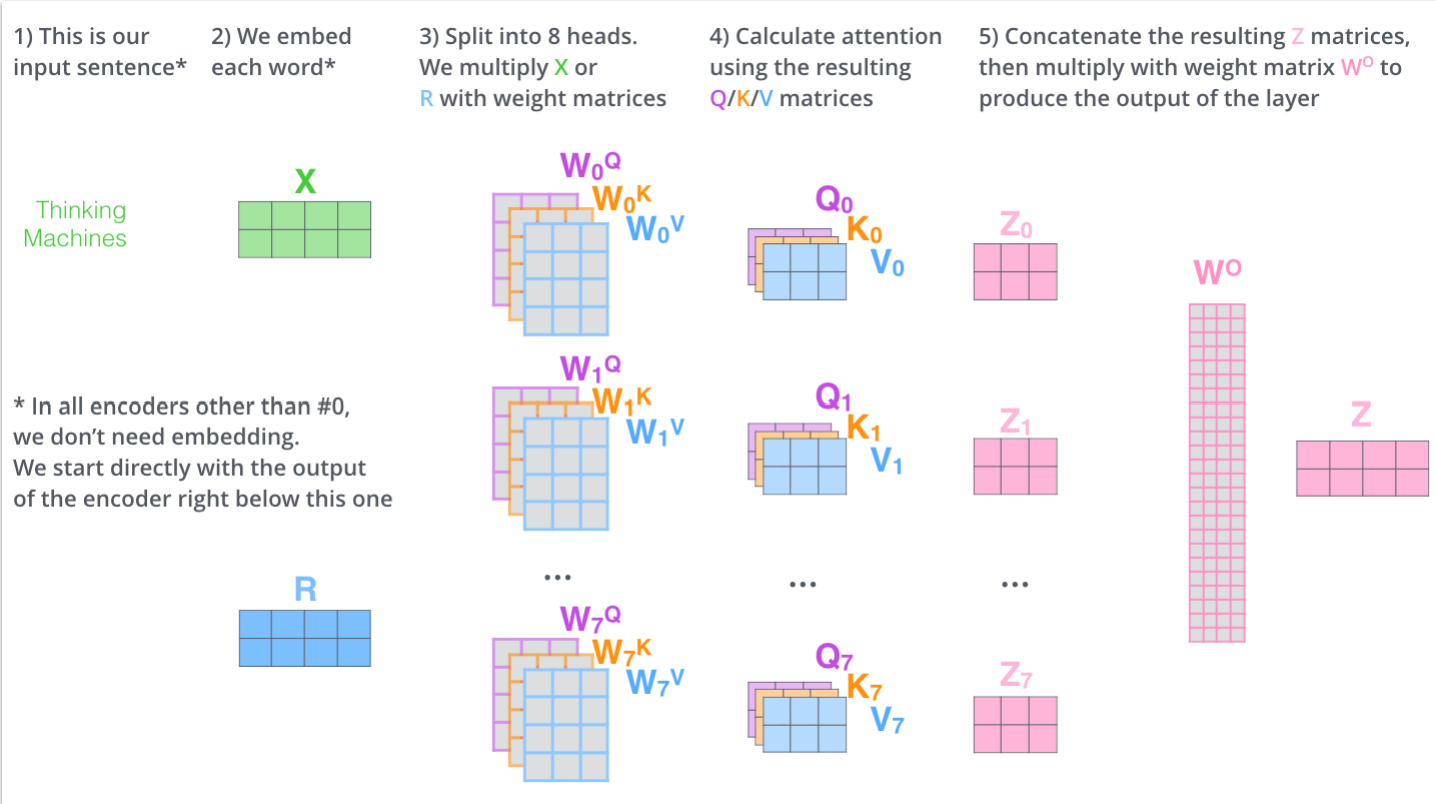
Transformer原理
From Attention to self-Attention
关于Attention基本原理我们在seq2seq中已经介绍过,简单说attention就是帮助我们找到两个序列之间的相关度,比如输出序列的每个输出分别应该关注输入序列的哪一部分, 也就是找到权重值 wi。
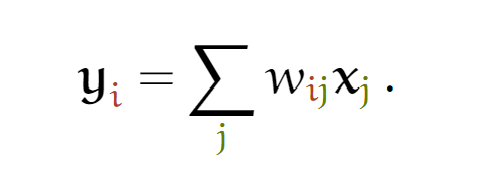
self-attention与attention的不同点在于,self-attention是帮助我们找到子序列与全局序列之间的关系,即self-attention使用的场景是同一序列内部,而attention是两个序列。
不过self-attention的计算方法与attention类似,同样可以使用上述公式(只不过这里的yi是同一序列中的某个token)。
wij的计算方式如下:
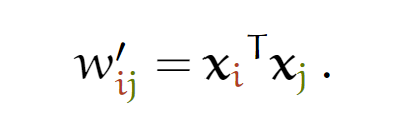
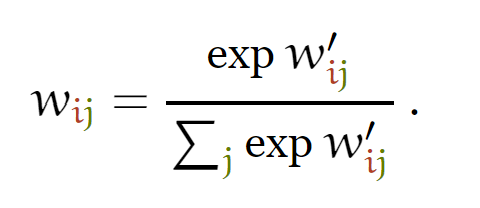
为了更好地理解这个公式,下面我给以y2的计算为例,给出计算过程(图中把exp漏掉了)和图例。
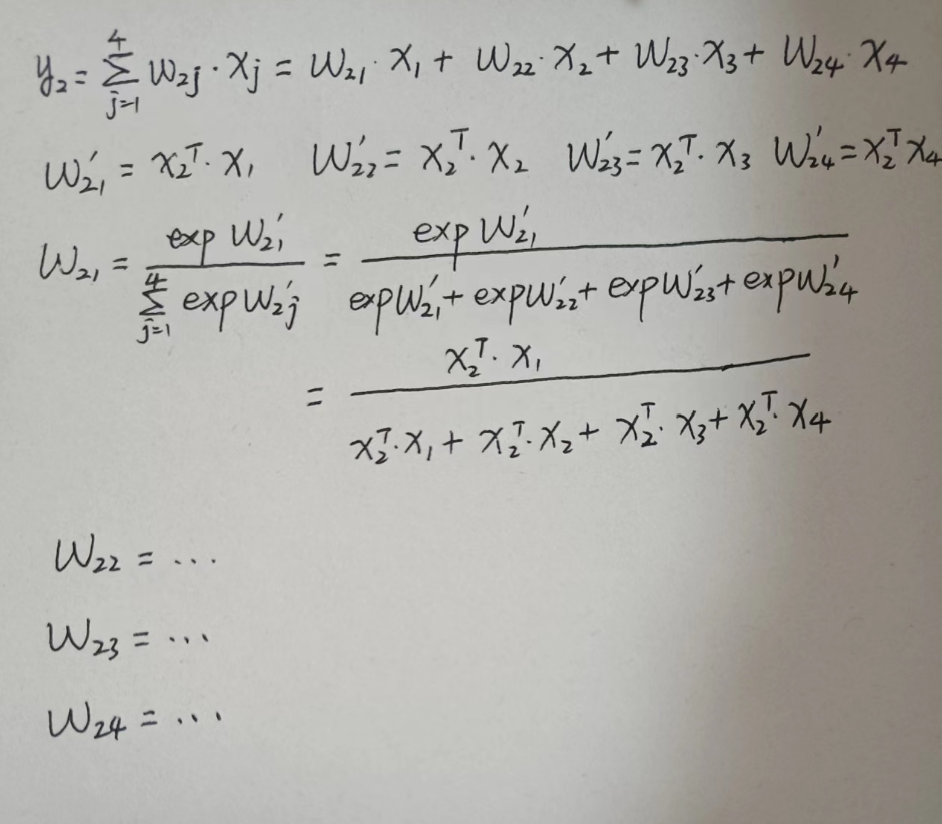
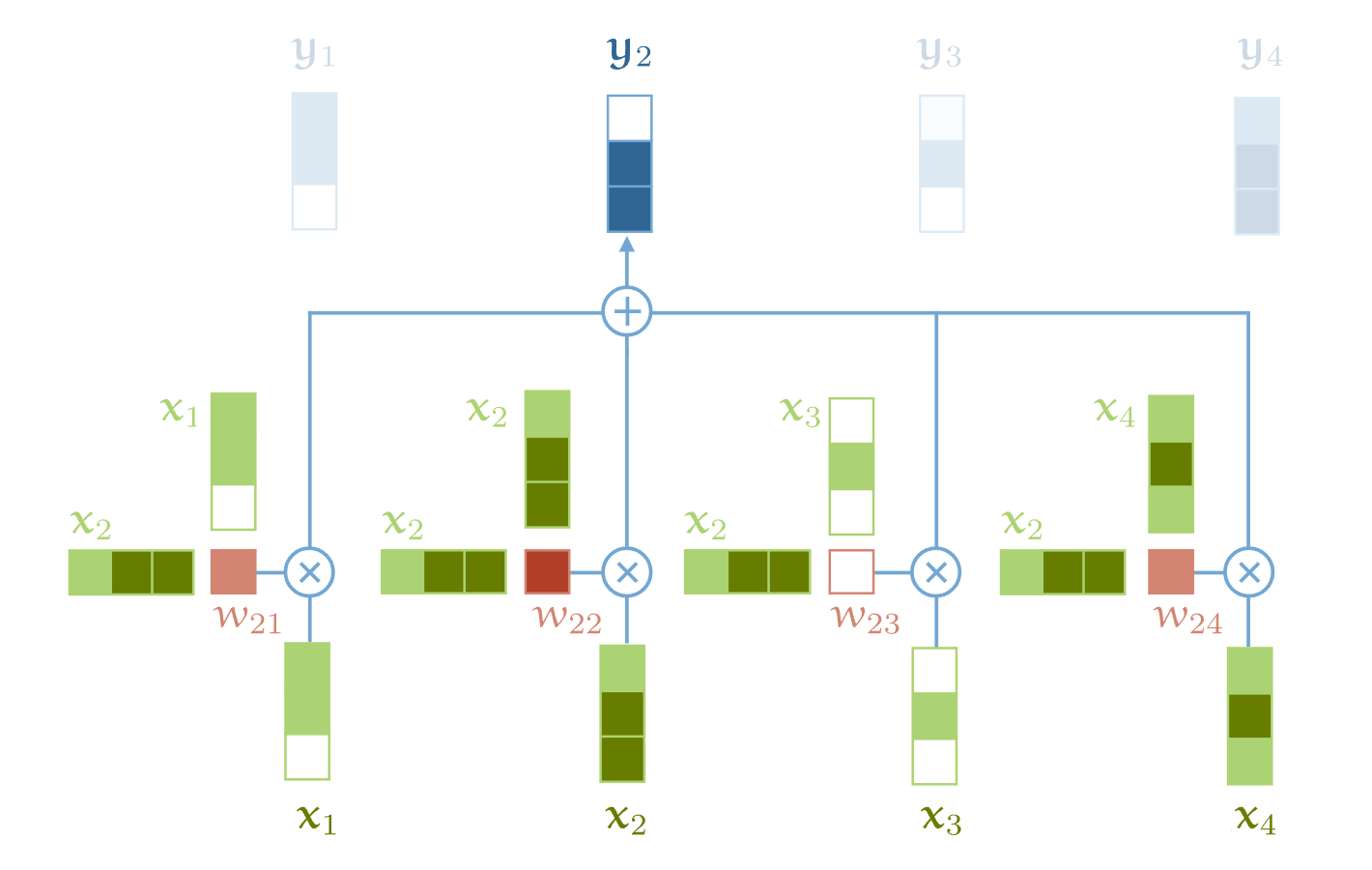
图中计算w省略了softmax操作。
Attention 和 Self-attention 的区别
- 在神经网络中,通常来说你会有输入层(Input),应用激活函数后的输出层(Output),在
RNN当中你会有状态(State)。如果 Attention (AT) 被应用在某一层的话,它更多的是被应用在输出或者是状态层上,而当我们使用 Self-attention(SA),这种注意力的机制更多的是在关注 Input 自己身上。 - Attention(AT)经常被应用在从编码器(encoder)转换到解码器(decoder)。比如说,解码器的神经元会接受一些AT从编码层生成的输入信息。在这种情况下,AT连接的是两个不同的组件(Component),编码器和解码器。但是如果我们用 SA,它就不是关注的两个组件,它只是在关注你应用的那一个组件。那这里他就不会去关注解码器了,就比如说在 Bert 中,使用的情况,我们就没有解码器。
- SA 可以在一个模型当中被多次的、独立的使用(比如说在 Transformer 中,使用了18次;在Bert当中使用 12次)。但是,AT 在一个模型当中经常只是被使用一次,并且起到连接两个组件的作用。
- SA 比较擅长在一个序列当中,寻找不同部分之间的关系。比如说,在词法分析的过程中,能够帮助去理解不同词之间的关系。AT 却更擅长寻找两个序列之间的关系,比如说在翻译任务当中,原始的文本和翻译后的文本。这里也要注意,在翻译任务中,SA 也很擅长,比如说 Transformer。
- AT 可以连接两种不同的模态,比如说图片和文字。SA 更多的是被应用在同一种模态上,但是如果一定要使用SA来做的话,也可以将不同的模态组合成一个序列,再使用 SA。
- 对我来说,大部分情况,SA 这种结构更加的 general,在很多任务作为降维、特征表示、特征交叉等功能尝试着应用,很多时候效果都不错。
Self-attention为什么可以work
为了应用 Self-attention,我们给每一个在词表中的单词 t 一个 Embeding 向量 vt (这个是我们通过一些 NLP 方法学习到的)。这也是我们在序列模型中常见的 Embeding Layer。它会把单词 the,cat,walks,on,the,street 转换成向量的形式
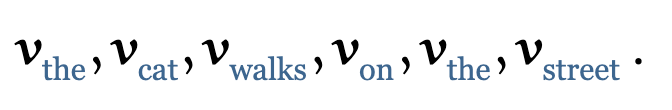
如果我们对这些向量序列进行 Self-attention的处理,那么就会生成一个新的向量序列
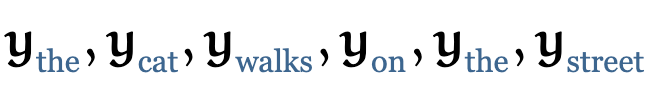
这其中 ycat 就是所有在第一个序列中的 Embedding 向量的加权和,权重值就是 vcat 的点积。
上文中我们也提到了, vt 是我们学习到的 Embedding 向量,它是 t 这个单词向量化的表示。在大部分的场景中, the 这个单词和句子中的其他单词没有很强的相关性,因此,我们就会期待 vthe 和其他单词的点积结果应该比较小或者是一个负值。那再看 walks 这个单词,为了能够解释这个单词,我们希望能够知道是谁在 walk ,那在这句话当中, vcat 和 vwalks 的点积就应该有一个比较大的正的值。
以上这些,就是在 Self-attention 背后一些直觉上的含义。点积操作很好的表示了输入语句中两个向量之间的相关性。
在我们继续下面的内容之前,非常有必要做一个小的总结。
- 到目前为止,我们还没有用到需要学习的参数。基础的 Self-attention 实际上完全取决于我们创建的输入序列,上游的 Embeding Layer 驱动着 Self-attention 学习对于文本语义的向量表示。
- Self-attention看到的序列只是一个集合(set),不是一个序列,它并没有顺序。如果我们重新排列集合,输出的序列也是一样的。后面我们要使用一些方法来缓和这种没有顺序所带来的信息的缺失。但是值得一提的是,Self-attention 本身是忽略序列的自然输入顺序的。
self-attention实现
上面我们也提到了,在这样一个模型当中,是没有使用到可以学习参数的,那我们能不能使用一些参数,来让整个结构更加的 flexable。就是由于这样的想法,诞生了query,key 和 value 这些参数。
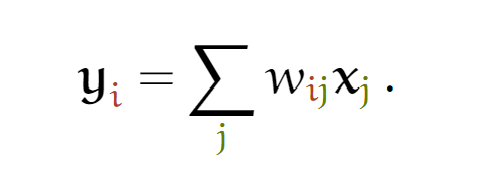
于是上面的计算方式扩展为下面这种:
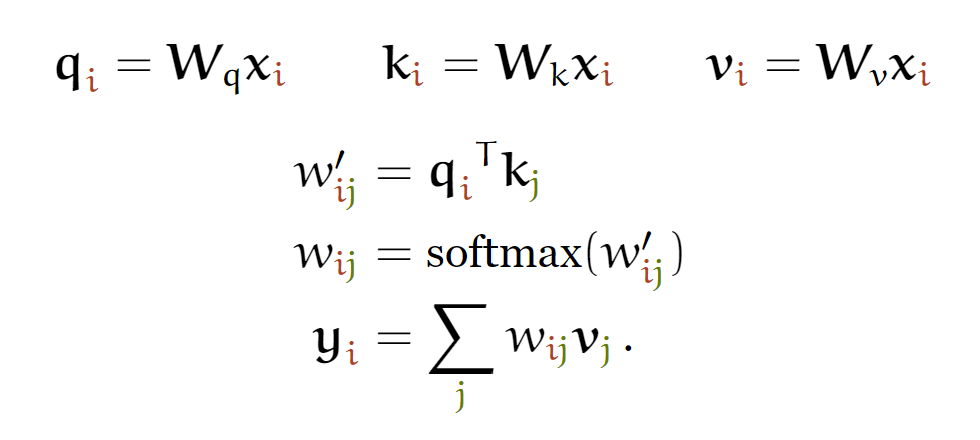
首先引入三个权重矩阵,Wq、Wk和Wv,与输入x的点乘分别计为query、key和value。这样后续的xi分别使用q、k和v来代替,也就是说实际上xi被使用了三次。
下面我们通过代码和图解的形式来描述self-attention的实现过程,可以进一步帮助理解。
第一步 准备输入
为了简单起见,我们使用3个输入,每个输入都是一个4维的向量。
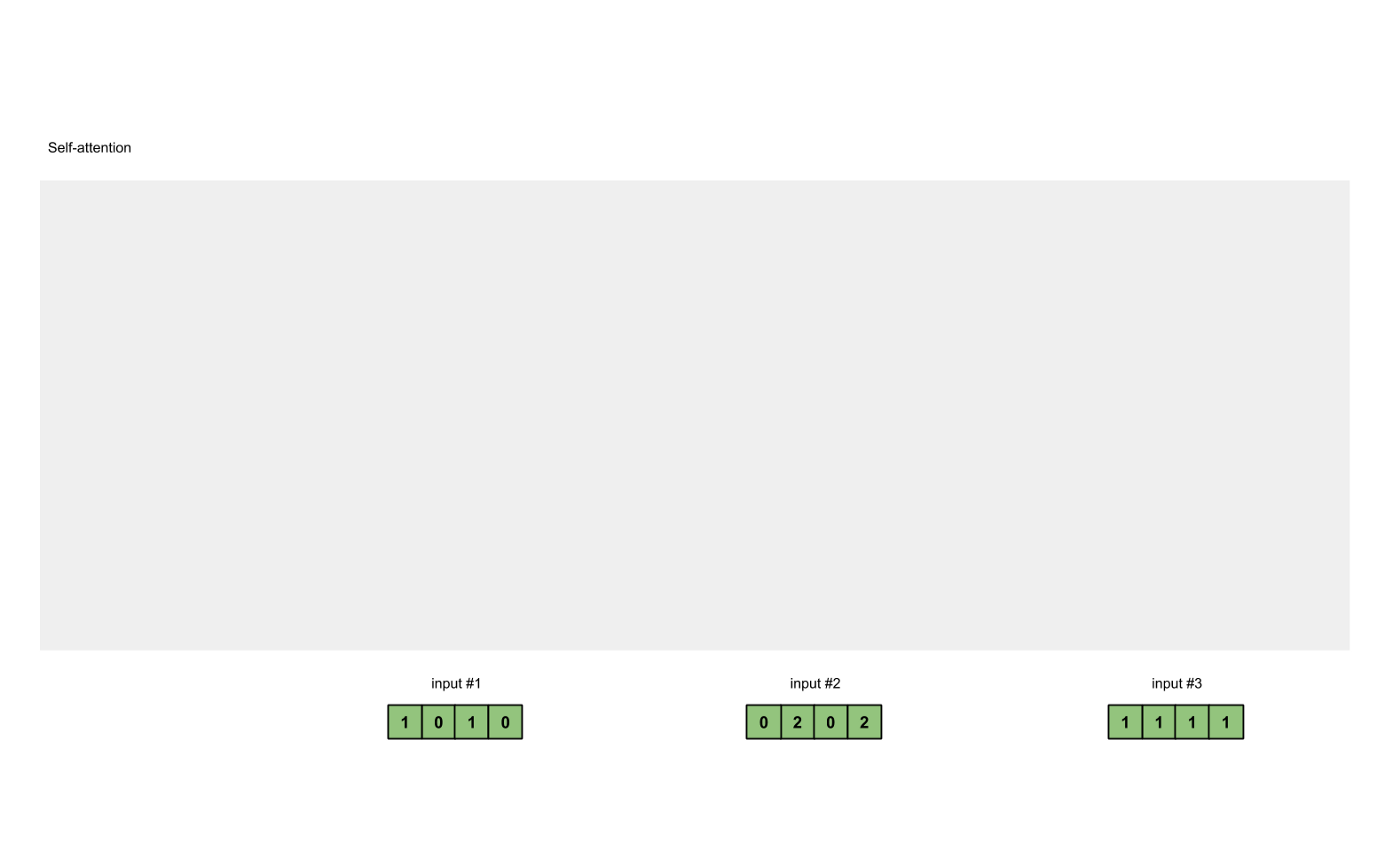
1 | x = [ |
第2步: 初始化参数
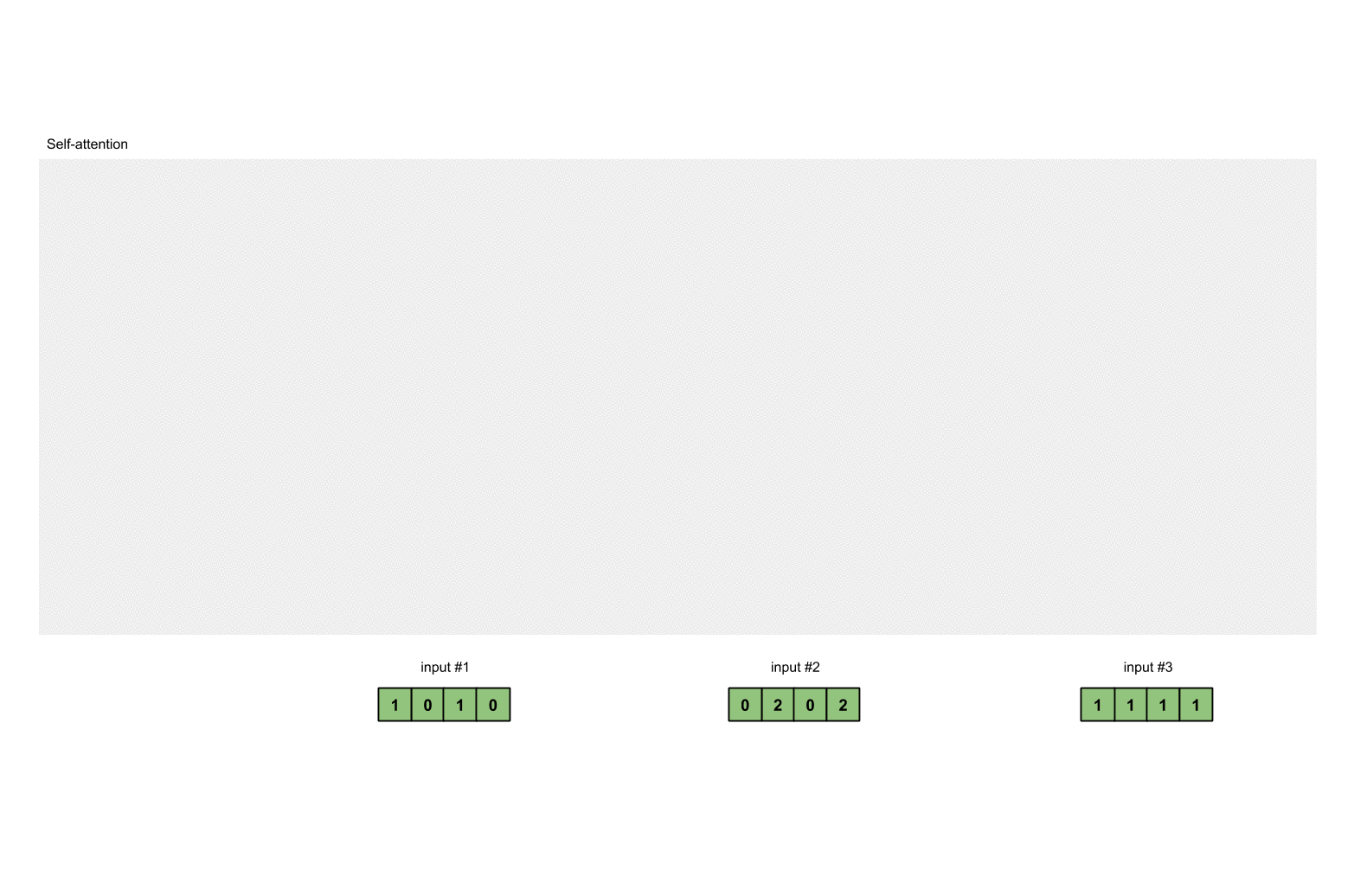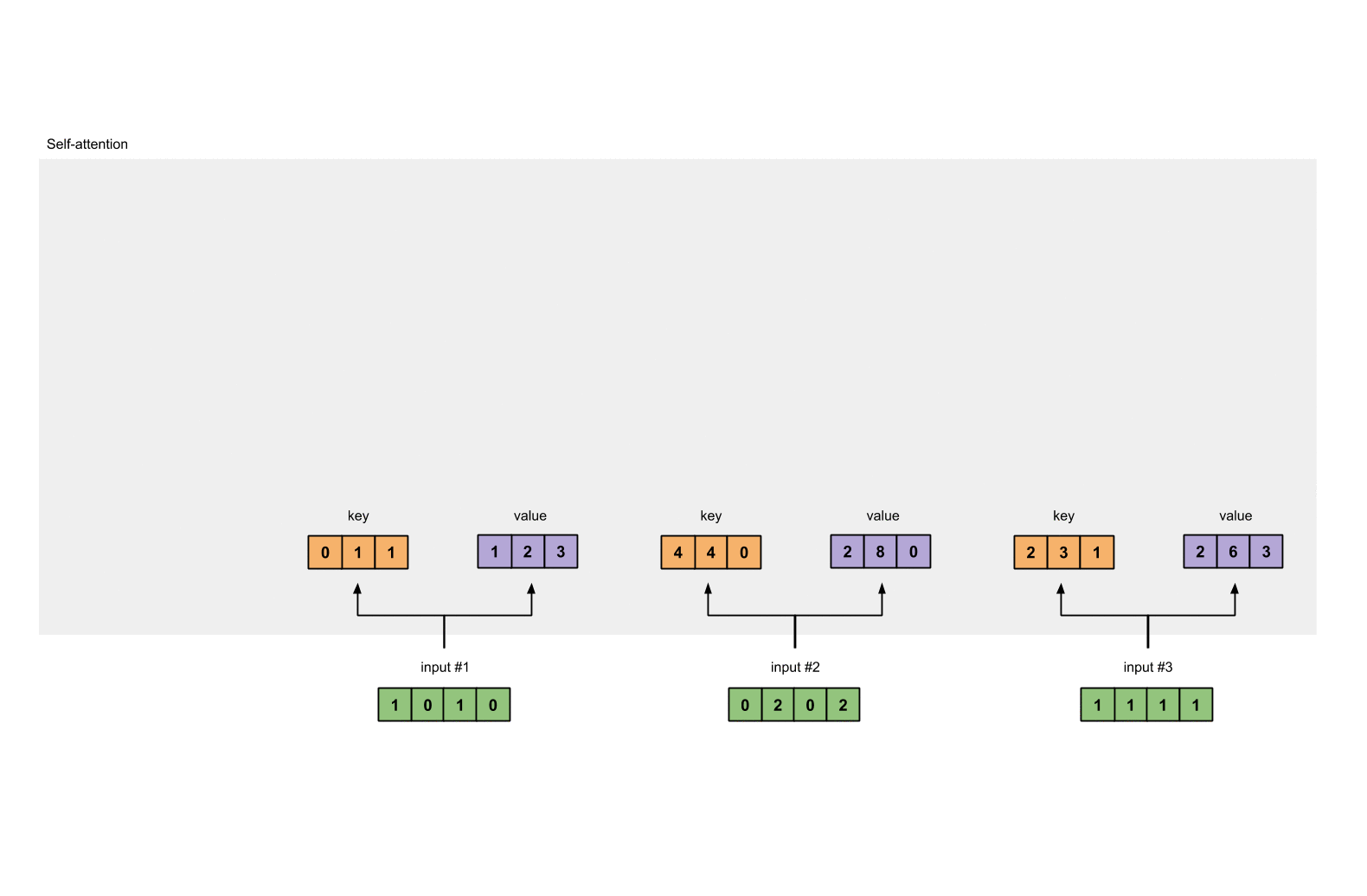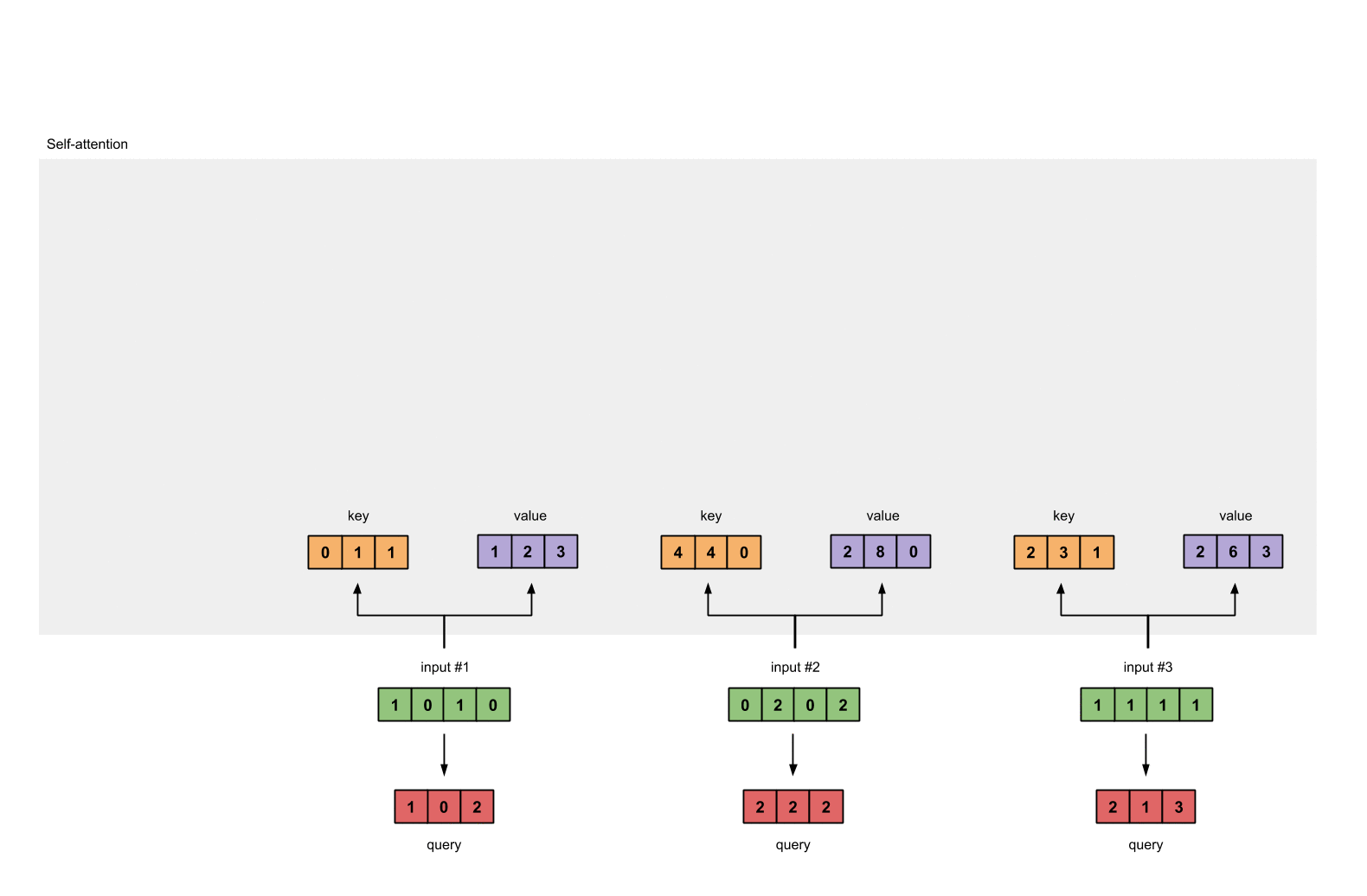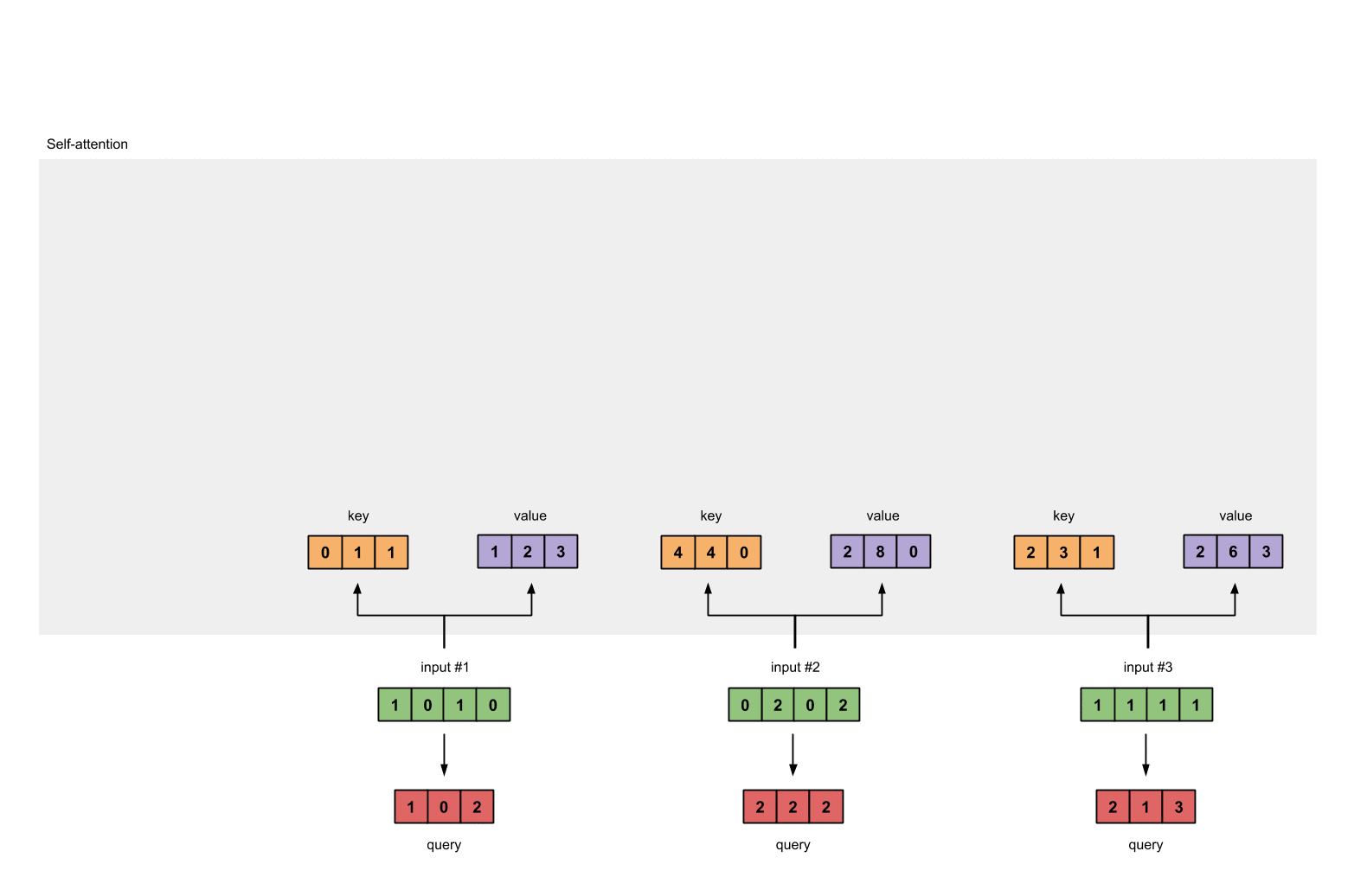
每一个输入都有三个表示,分别为key(橙黄色)query(红色)value(紫色)。比如说,每一个表示我们希望是一个3维的向量。由于输入是4维,所以我们的参数矩阵为 4*3 维。
后面我们会看到,value的维度,同样也是我们输出的维度。
为了能够获取这些表示,每一个输入(绿色)要和key,query和value相乘,在我们例子中,我们使用如下的方式初始化这些参数。
1 | w_key = [ |
Note: 通常在神经网络的初始化过程中,这些参数都是比较小的,一般会在Gaussian, Xavier and Kaiming distributions随机采样完成。
第3步:获取key,query和value
 现在我们有了三个参数,让我们来获取实际上的key,query和value。
现在我们有了三个参数,让我们来获取实际上的key,query和value。
keys的表示为:
1 | [0, 0, 1] |
values的表示为:
1 | [0, 2, 0] |
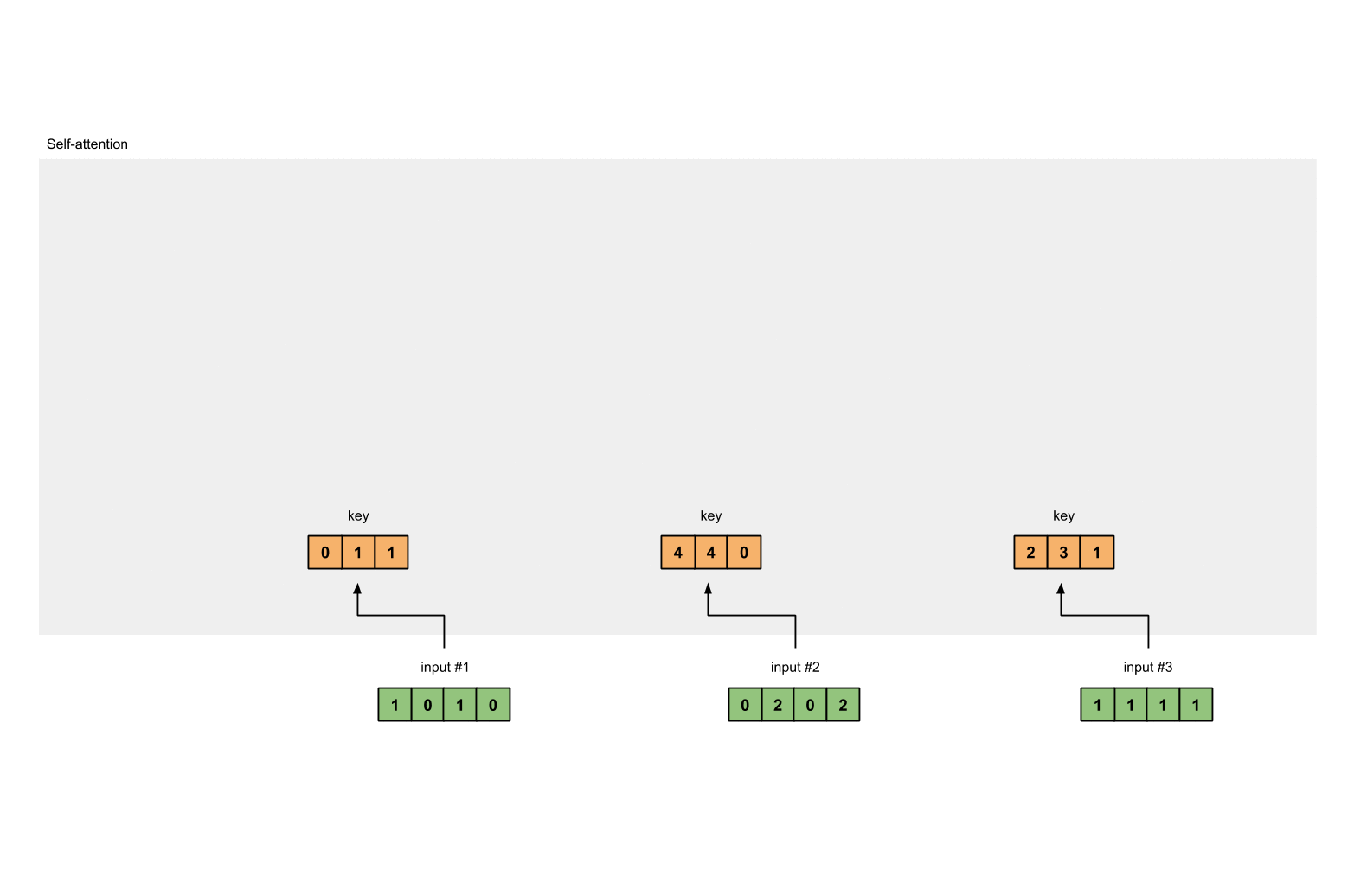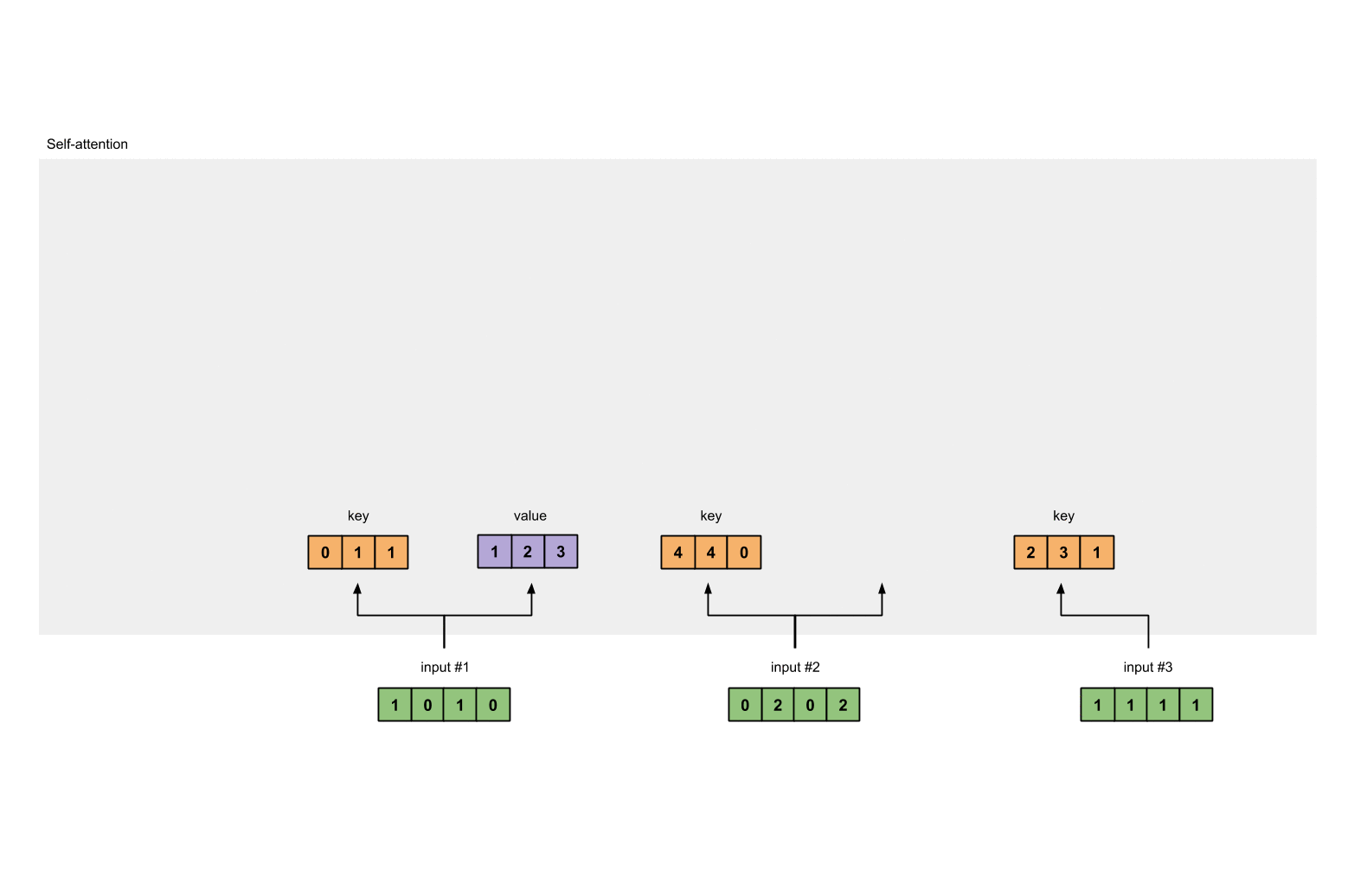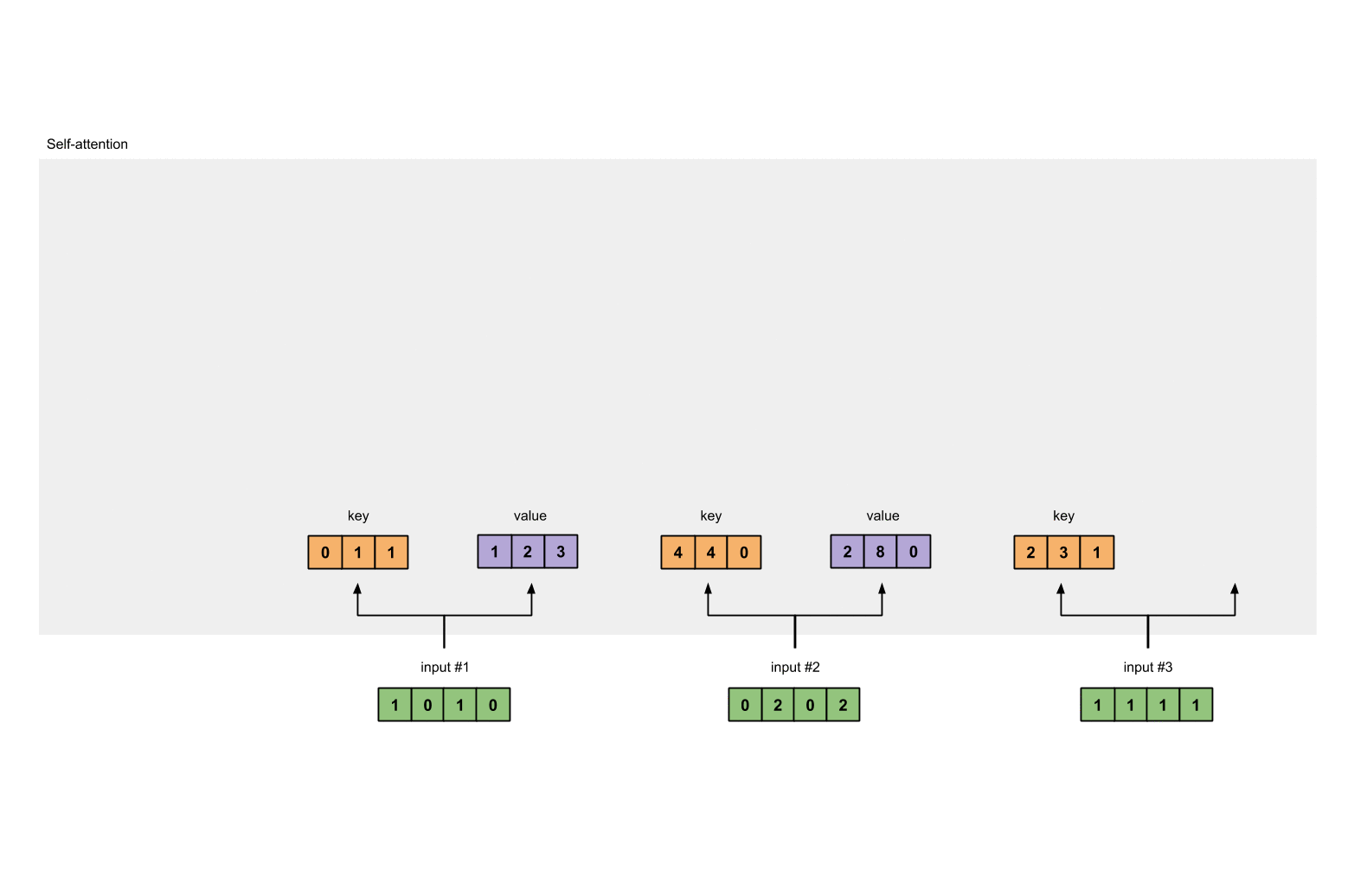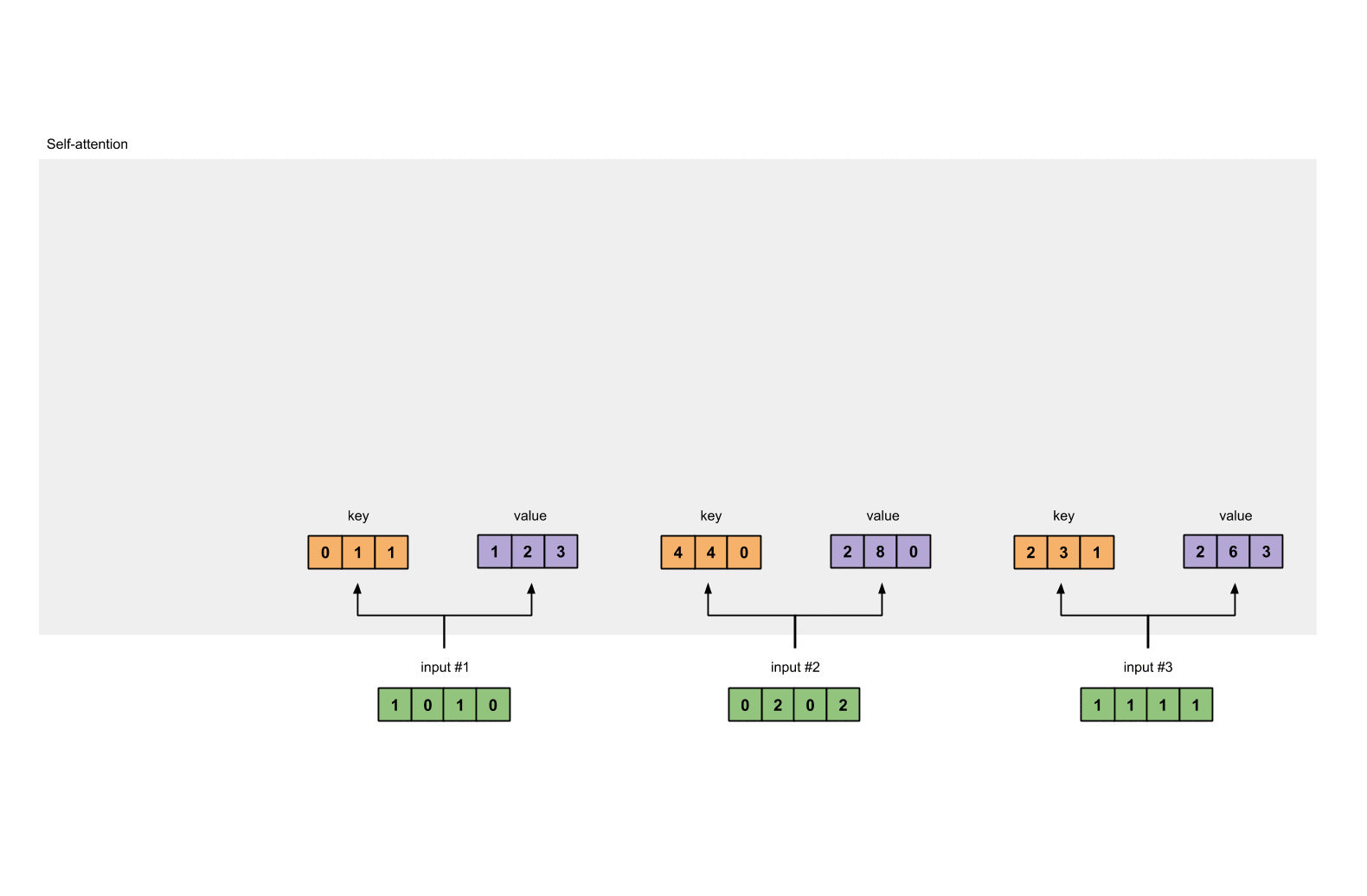
querys的表示为:
1 | [1, 0, 1] |
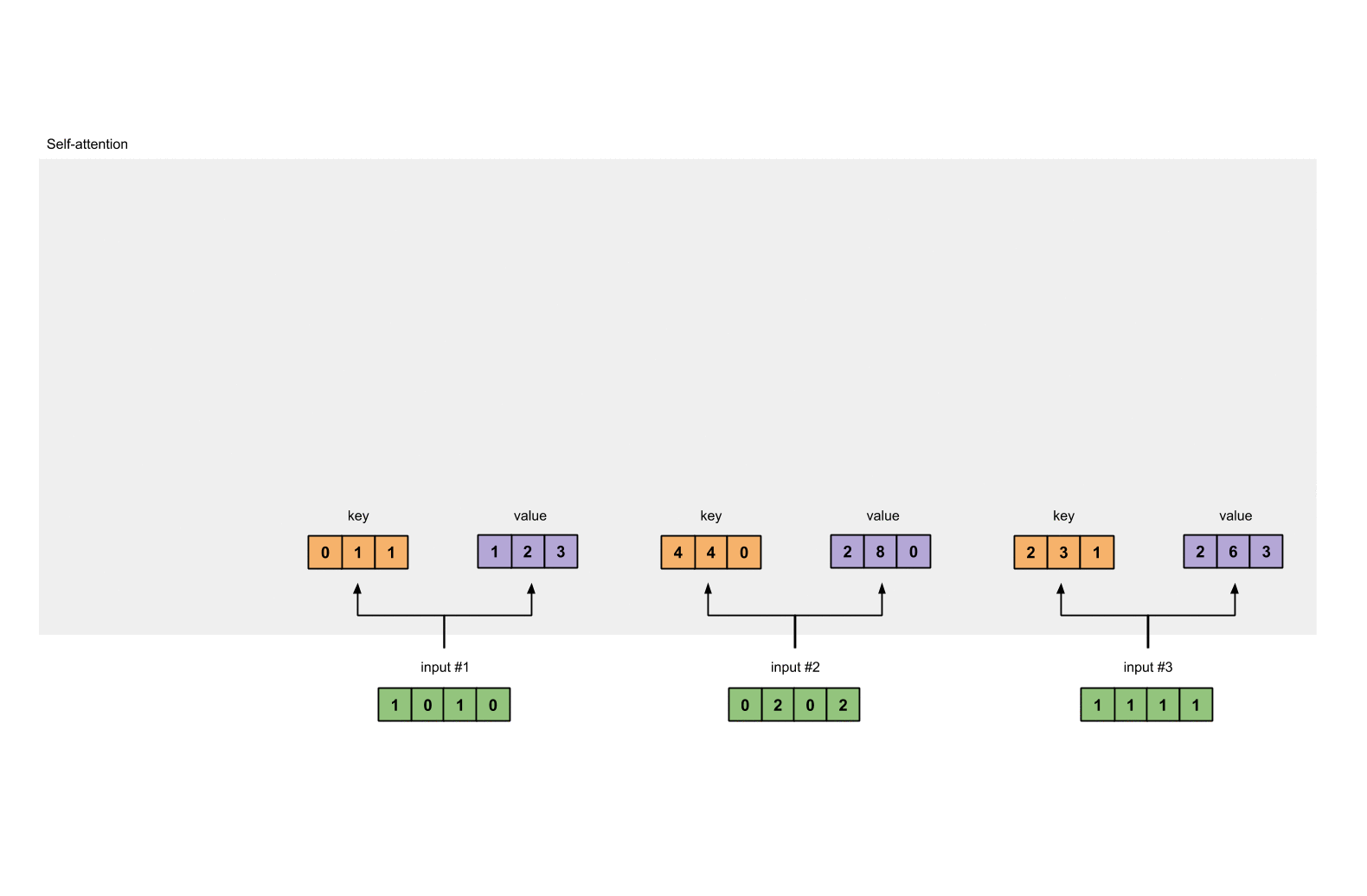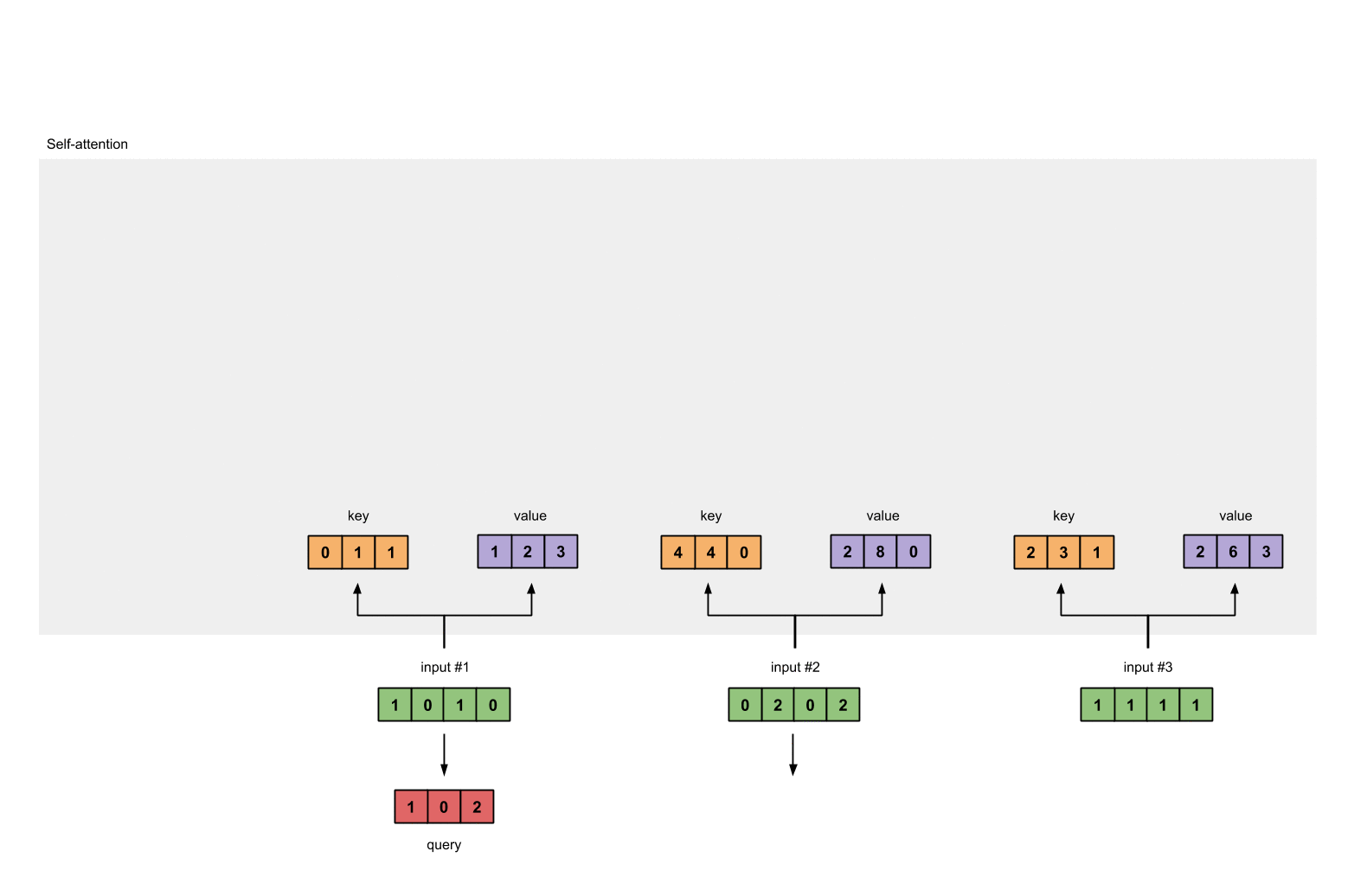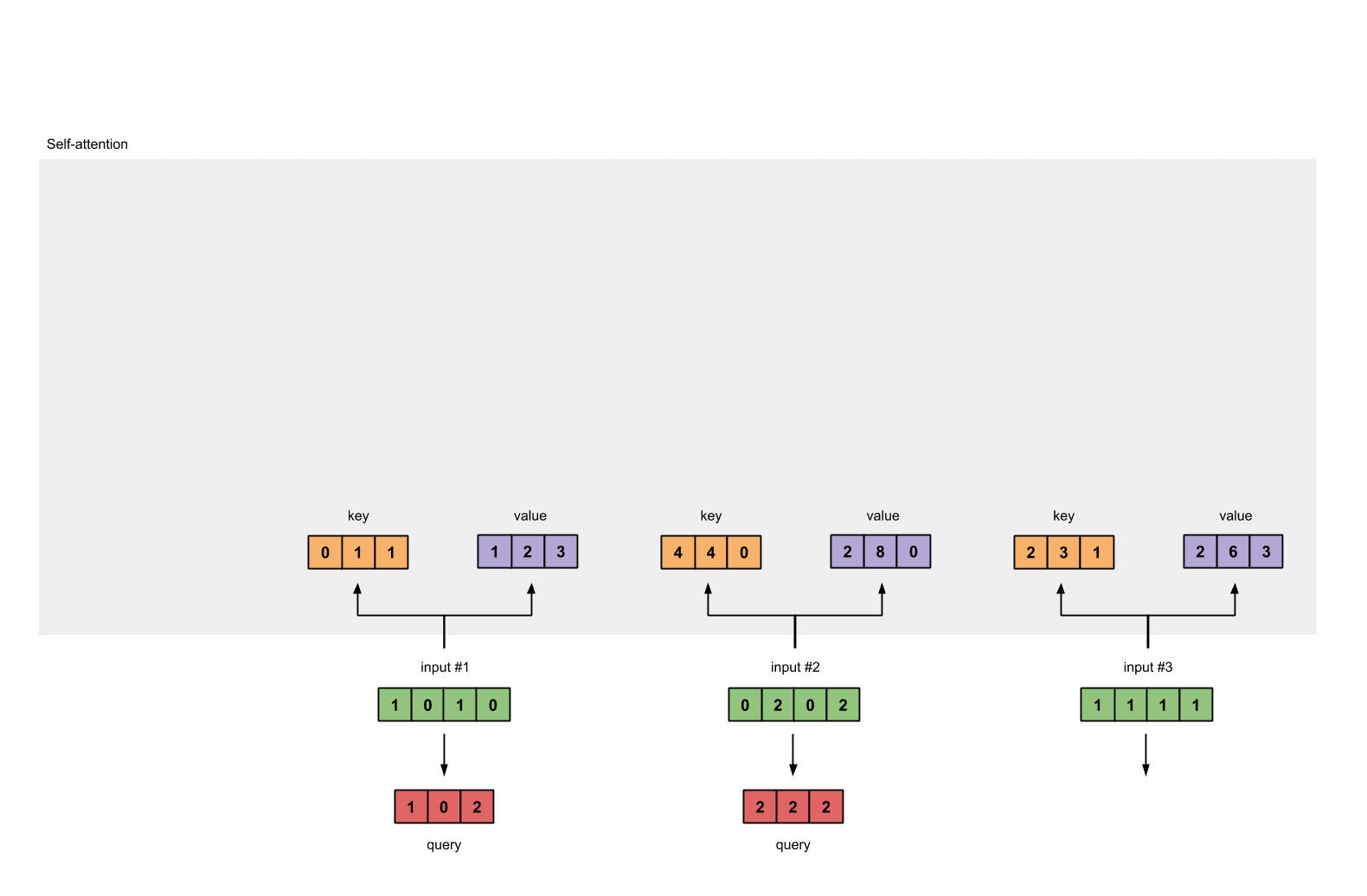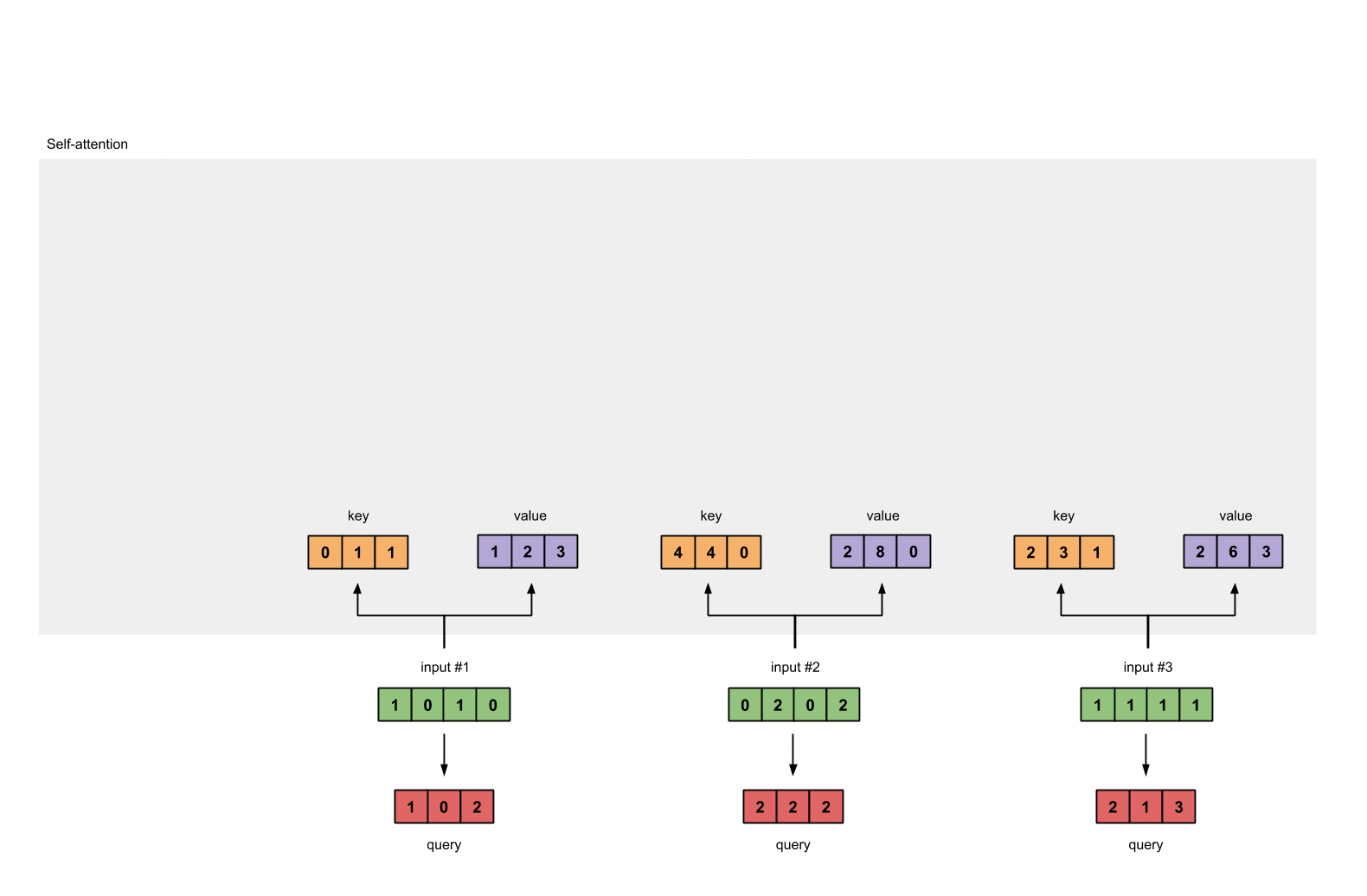
Notes: 在我们实际的应用中,有可能会在点乘后,加上一个bias的向量。
1 | keys = x @ w_key |
第4步: 计算 attention scores(以input1为例)
这里图形给出的是Input1的计算方式,在代码层面input1、input2和Input3实际是同时进行的。
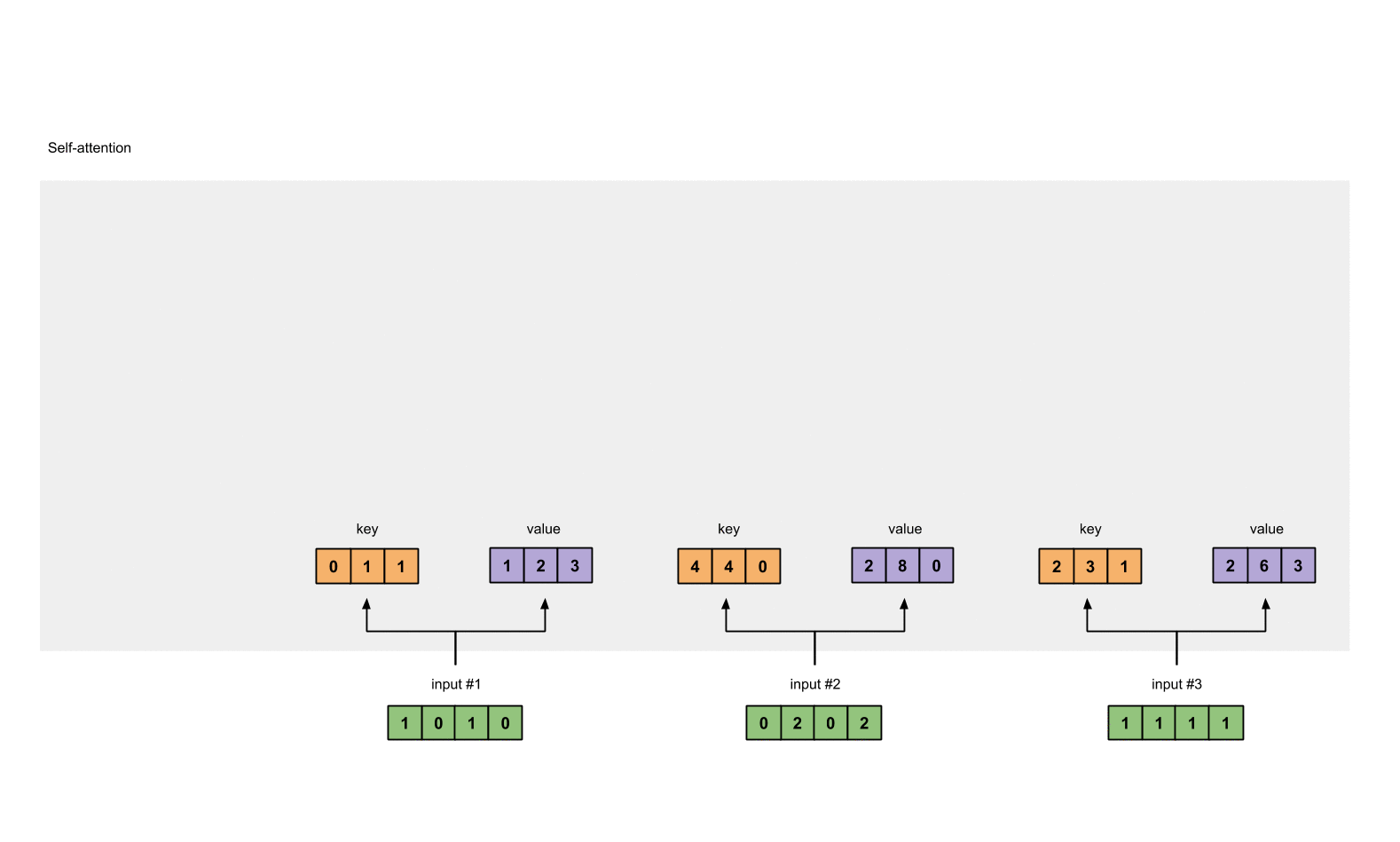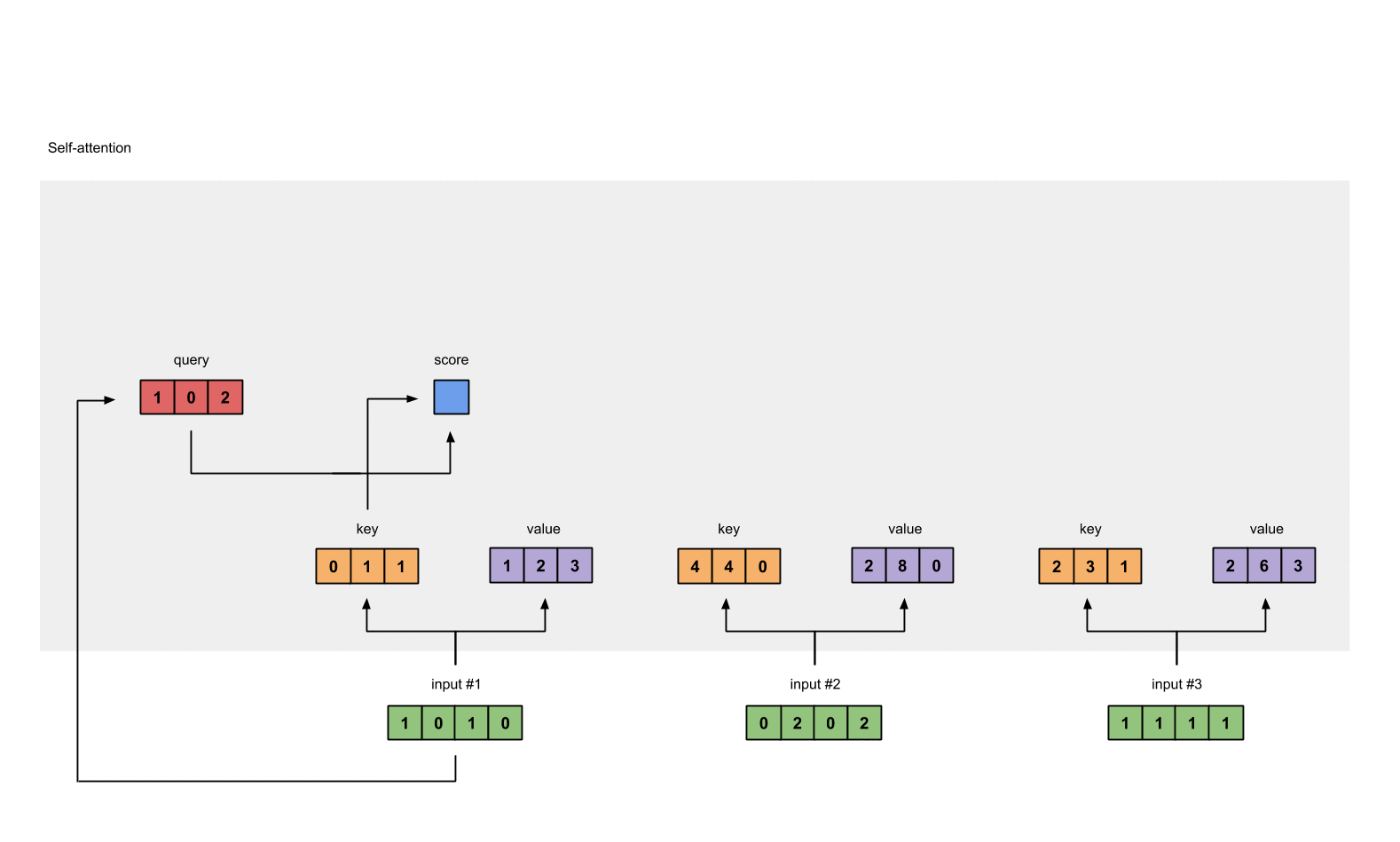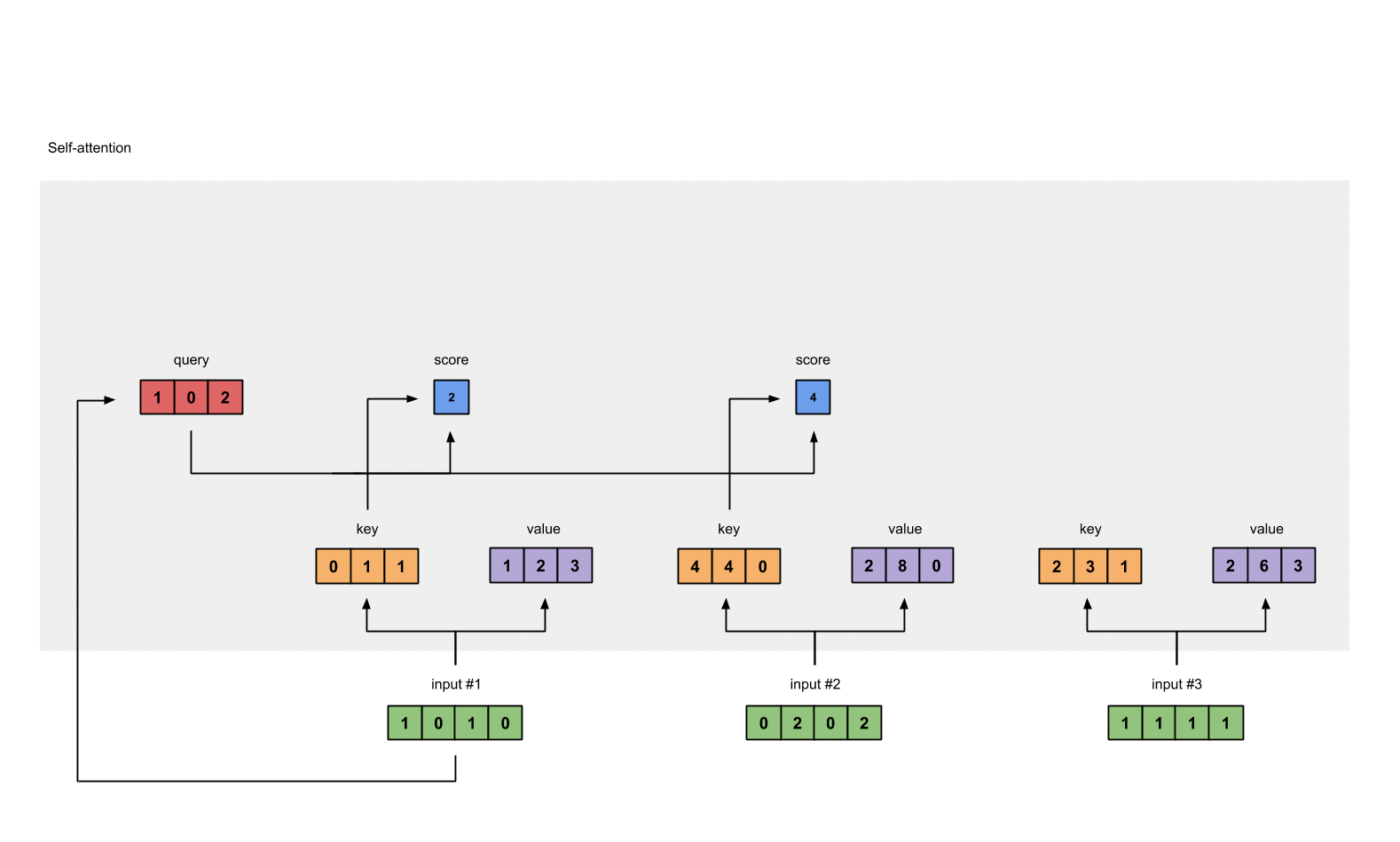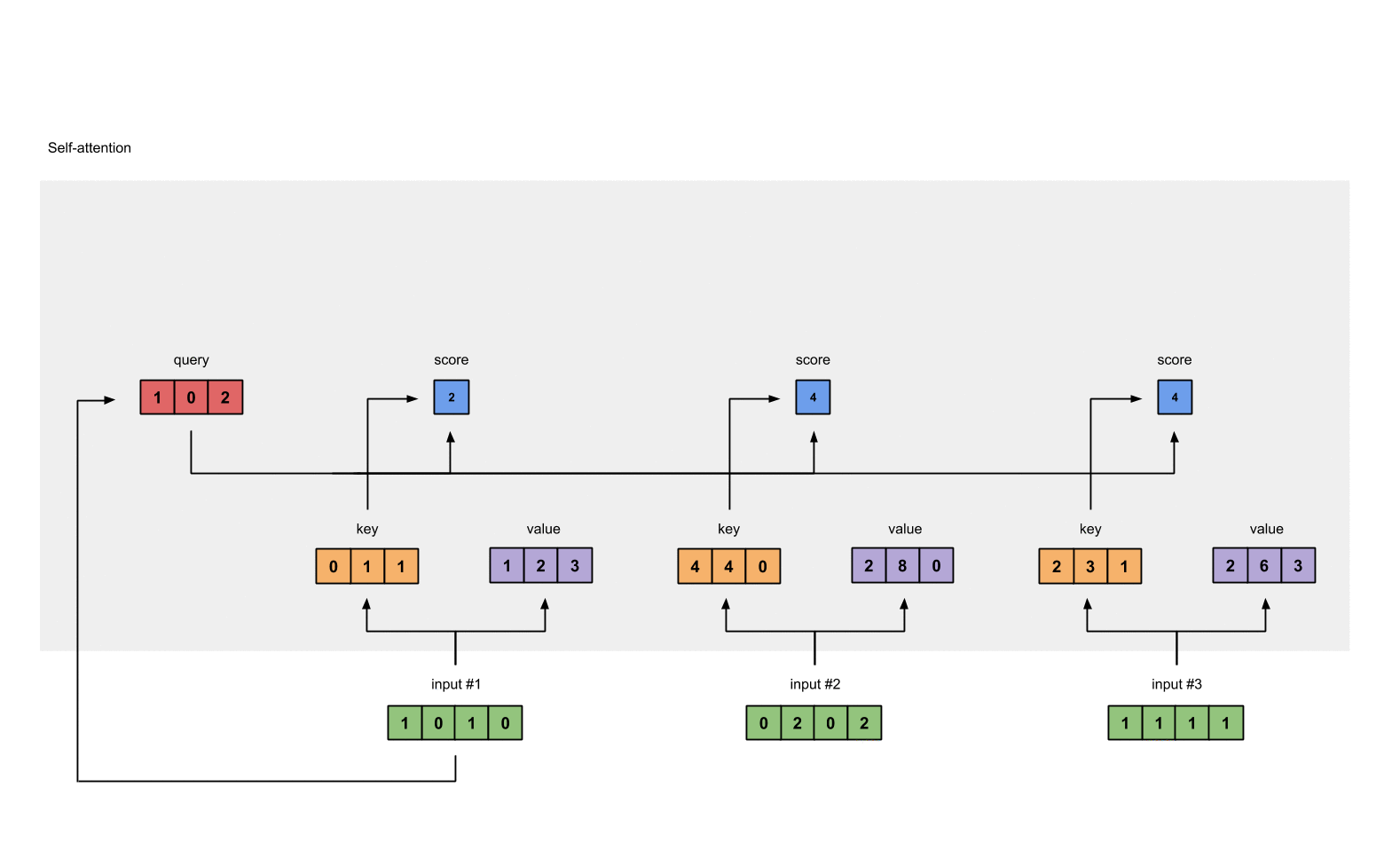
为了获取input1的attention score,我们使用点乘来处理所有的key和query,包括它自己的key和value。这样我们就能够得到3个key的表示(因为我们有3个输入),我们就获得了3个attention score(蓝色)。
1 | [0, 4, 2] |
这里我们需要注意一下,这里我们只有input1的例子。后面,我们会对其他的输入的query做相同的操作。
这里计算input1的attention score使用的是input1的query,计算input2和input3时,只需要分别使用input2和input3的query即可,其他步骤一致。(在实际计算时,利用矩阵相乘,多个Input的score可以同时计算)
1 | # 在上面的式子中是,qT x k |
第5步: 计算softmax
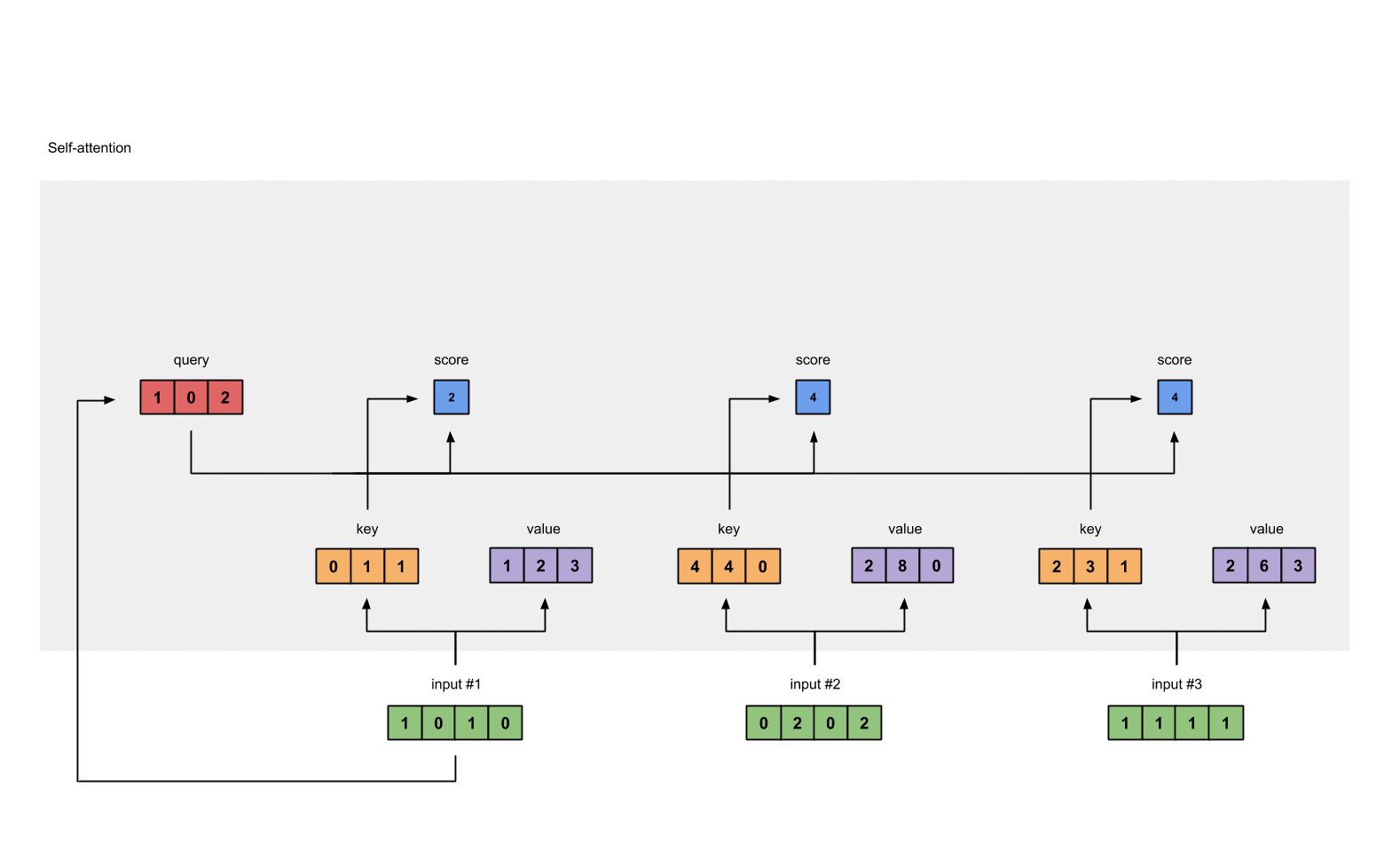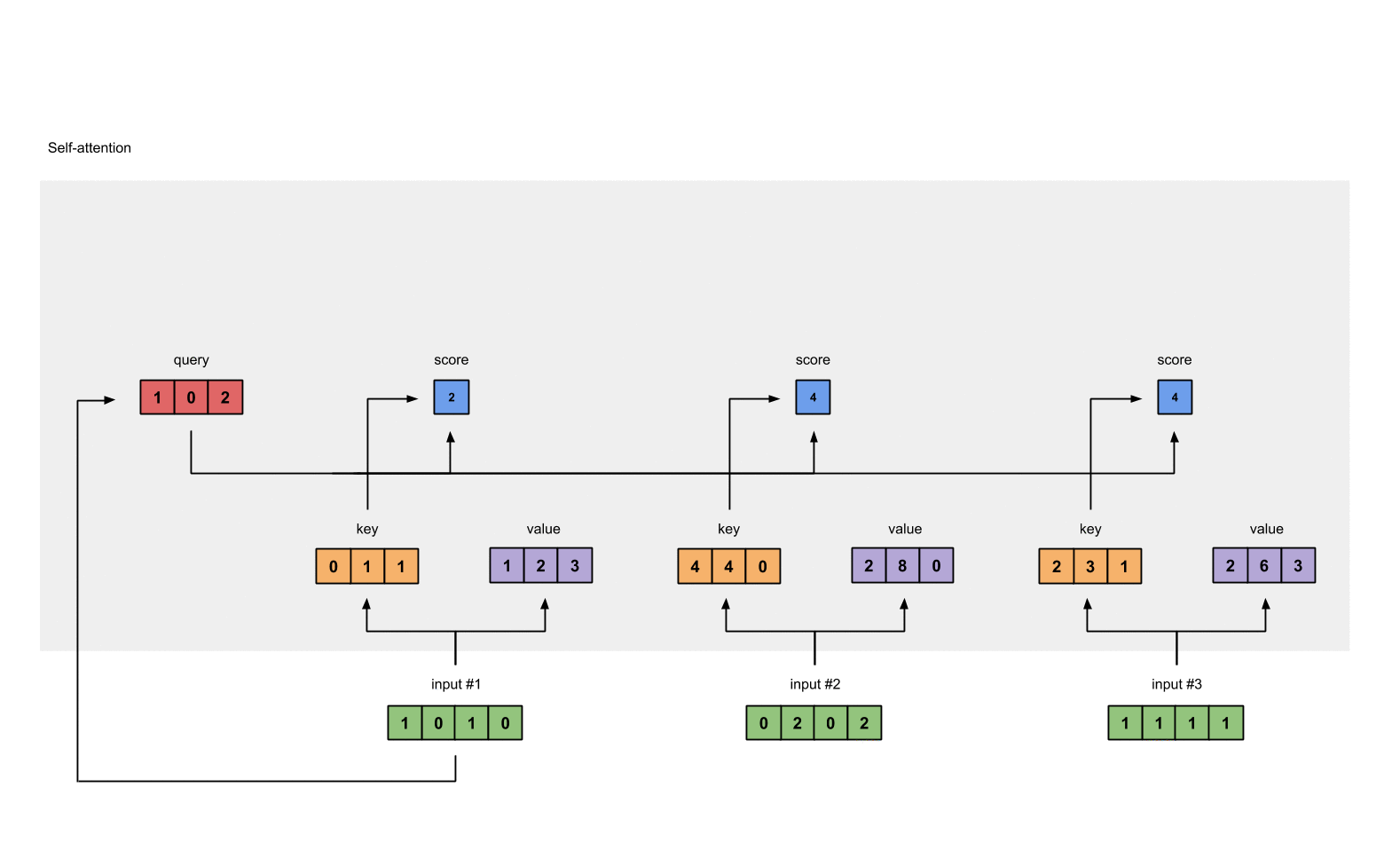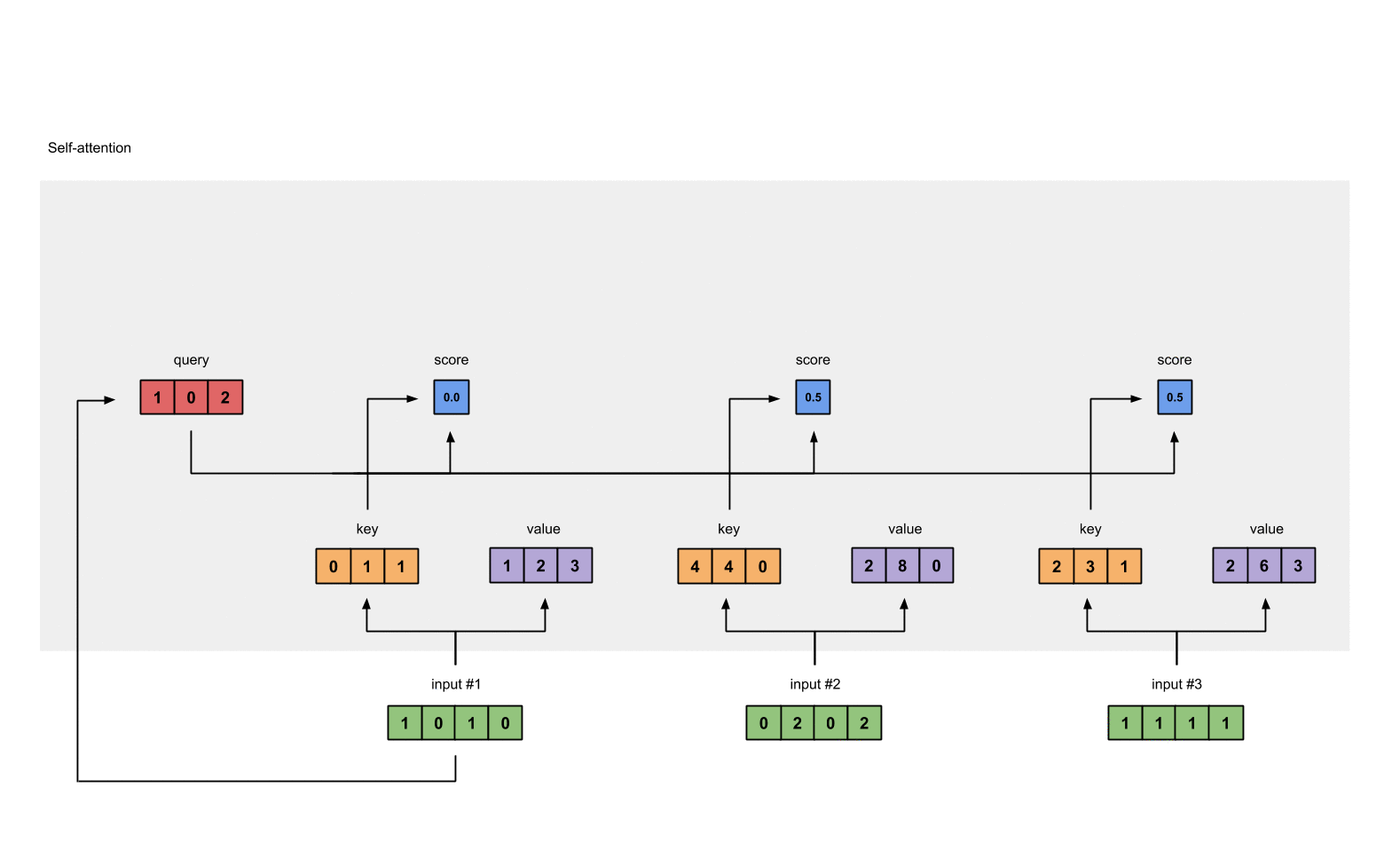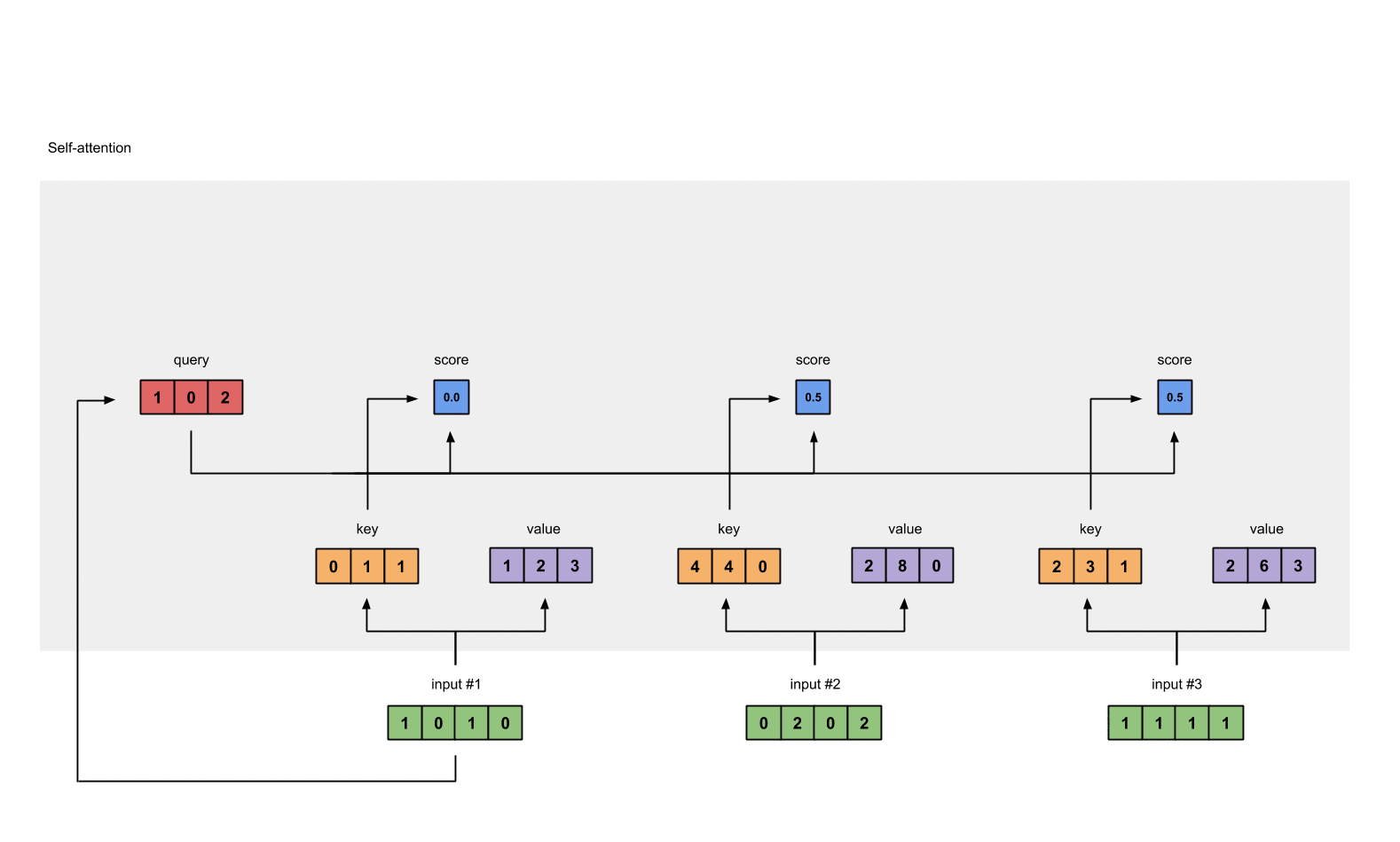
给attention score应用softmax。
1 | softmax([2, 4, 4]) = [0.0, 0.5, 0.5] # 这里是近似的结果 |
1 | from torch.nn.functional import softmax |
第6步: 给value乘上score
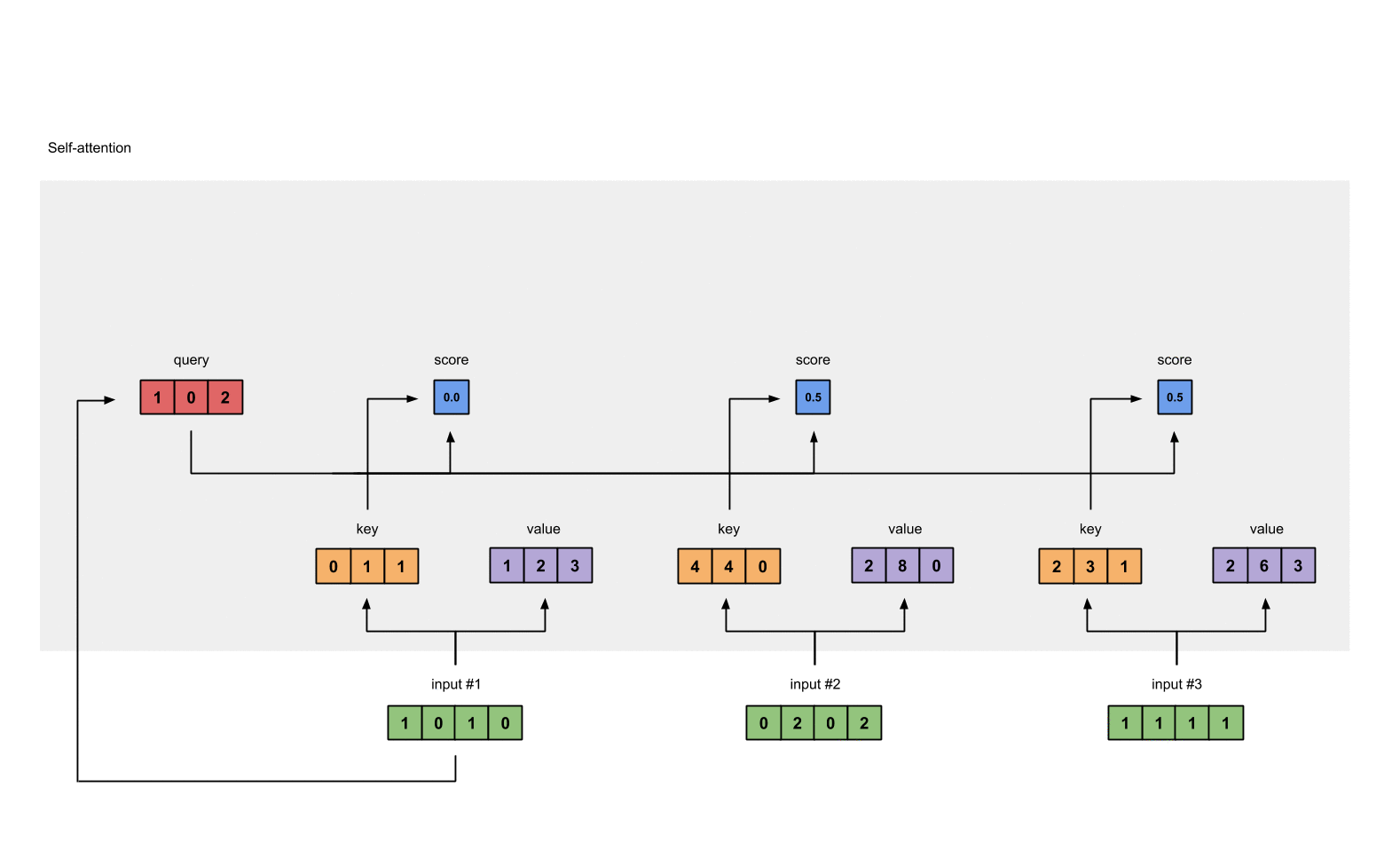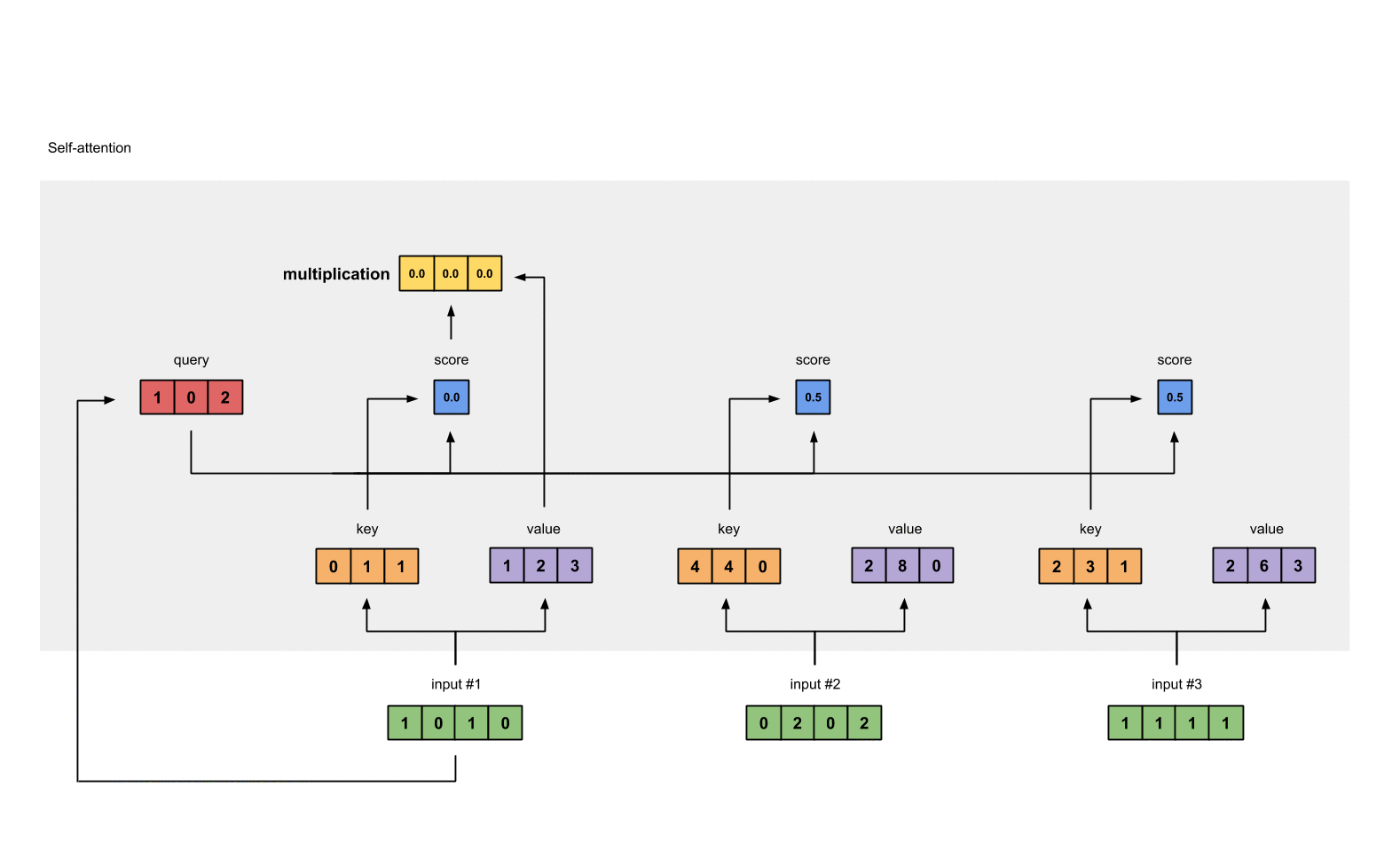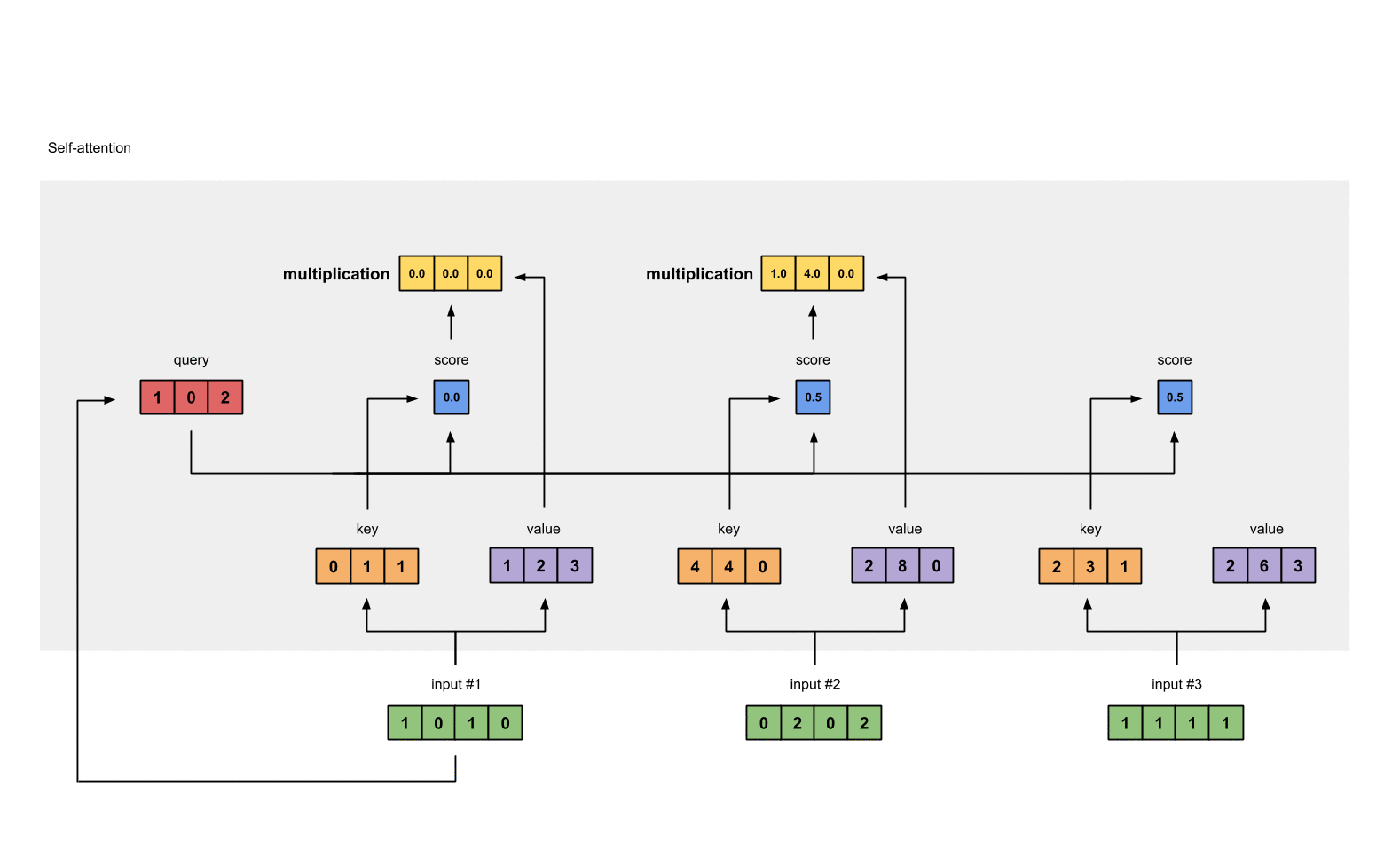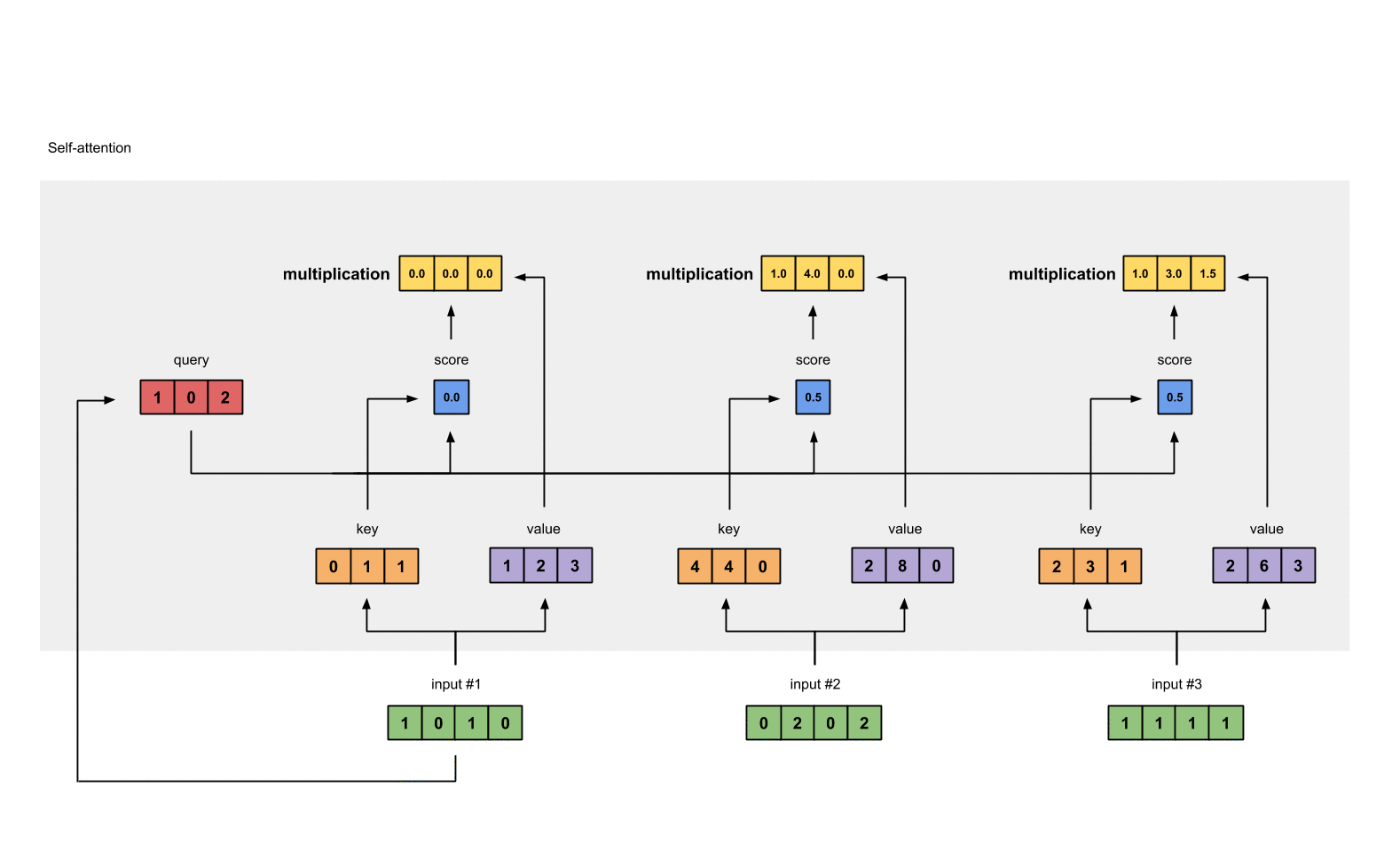
使用经过softmax后的attention score乘以它对应的value值(紫色),这样我们就得到了3个weighted values(黄色)。
1 | 1: 0.0 * [1, 2, 3] = [0.0, 0.0, 0.0] |
1 | weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None] |
values[:, None]
1 | <tf.Tensor: shape=(3, 1, 3), dtype=float32, numpy= |
attn_scores_softmax.T[:,:,None]
1 | <tf.Tensor: shape=(3, 3, 1), dtype=float32, numpy= |
第7步: 给value加权求和获取output
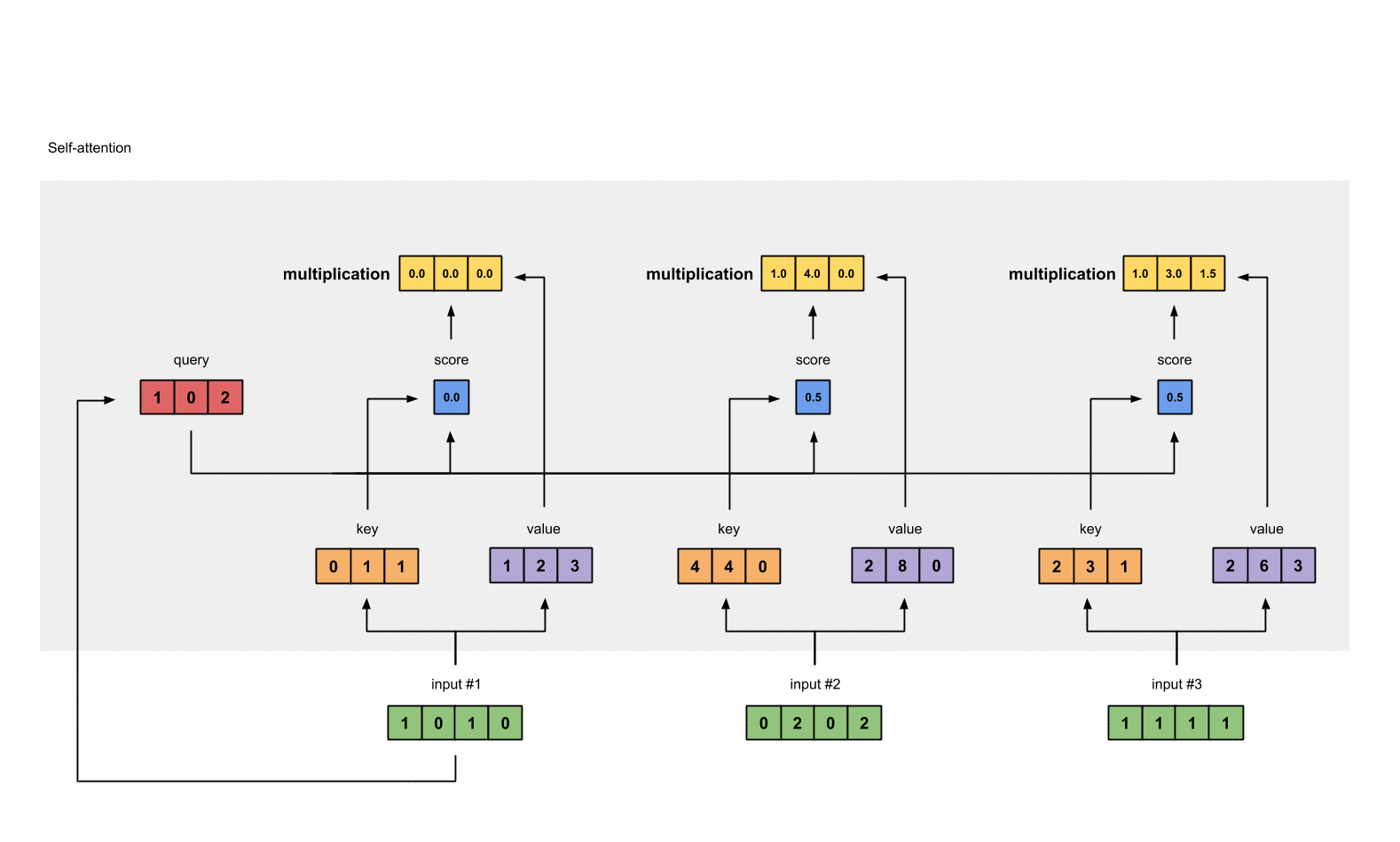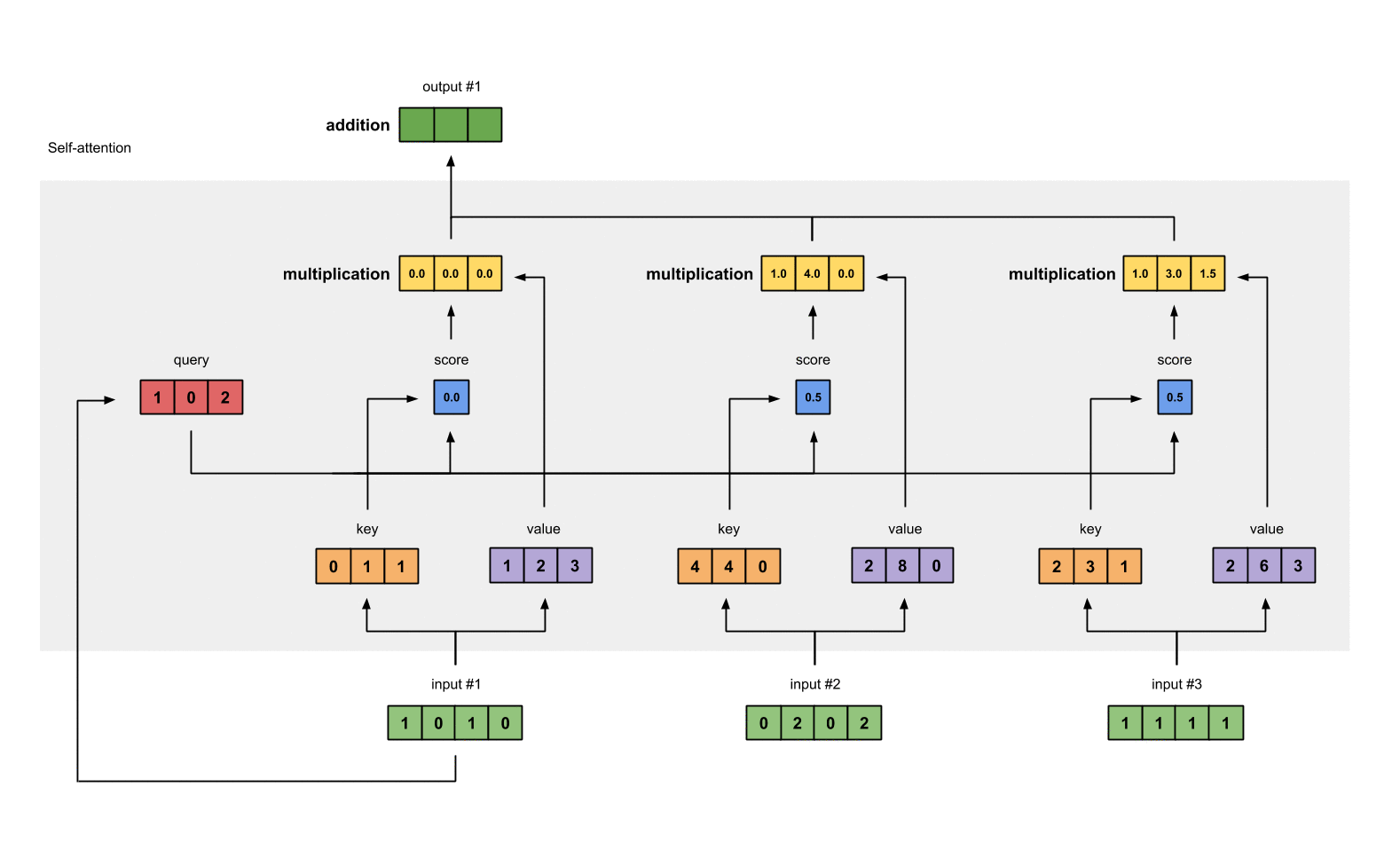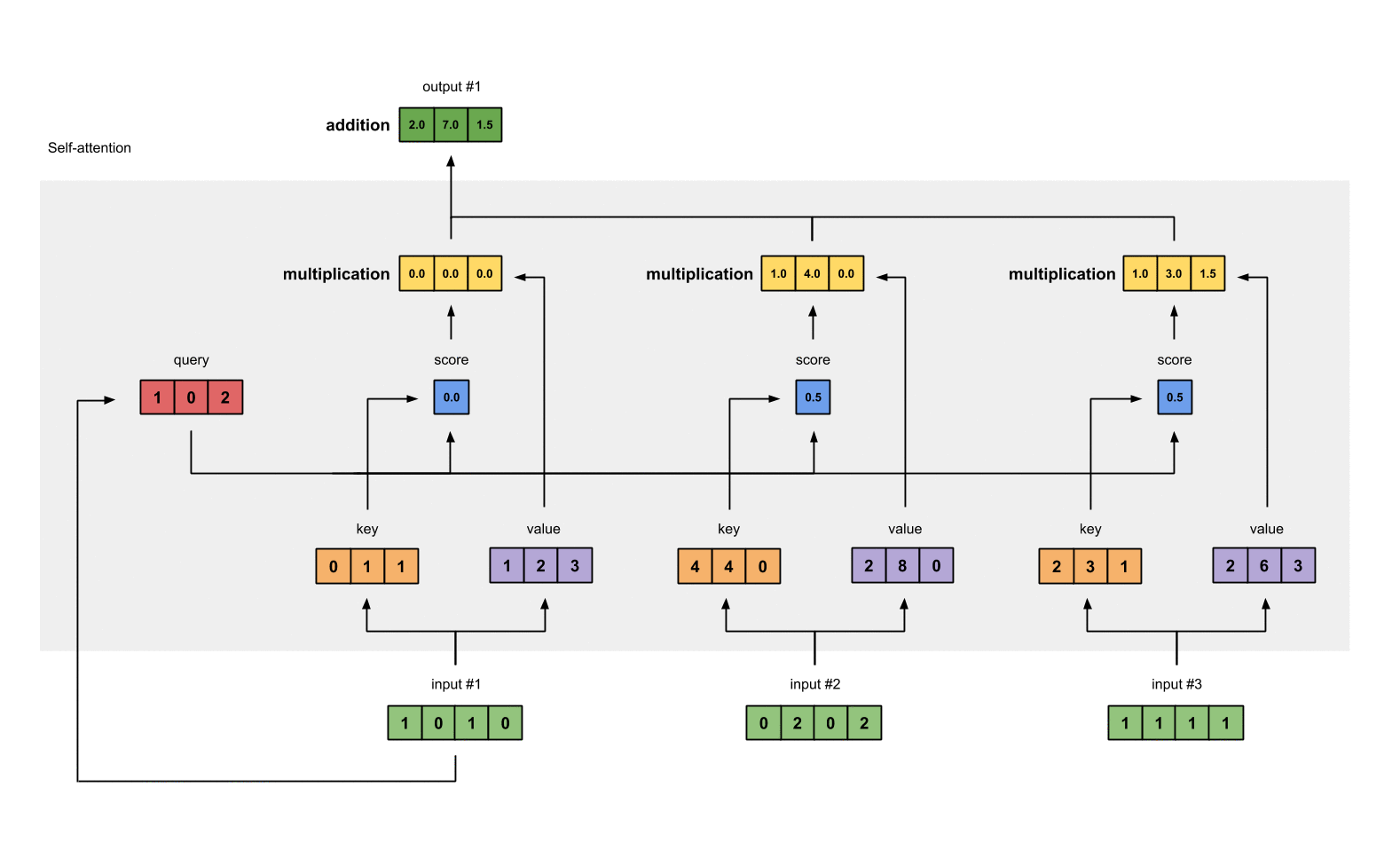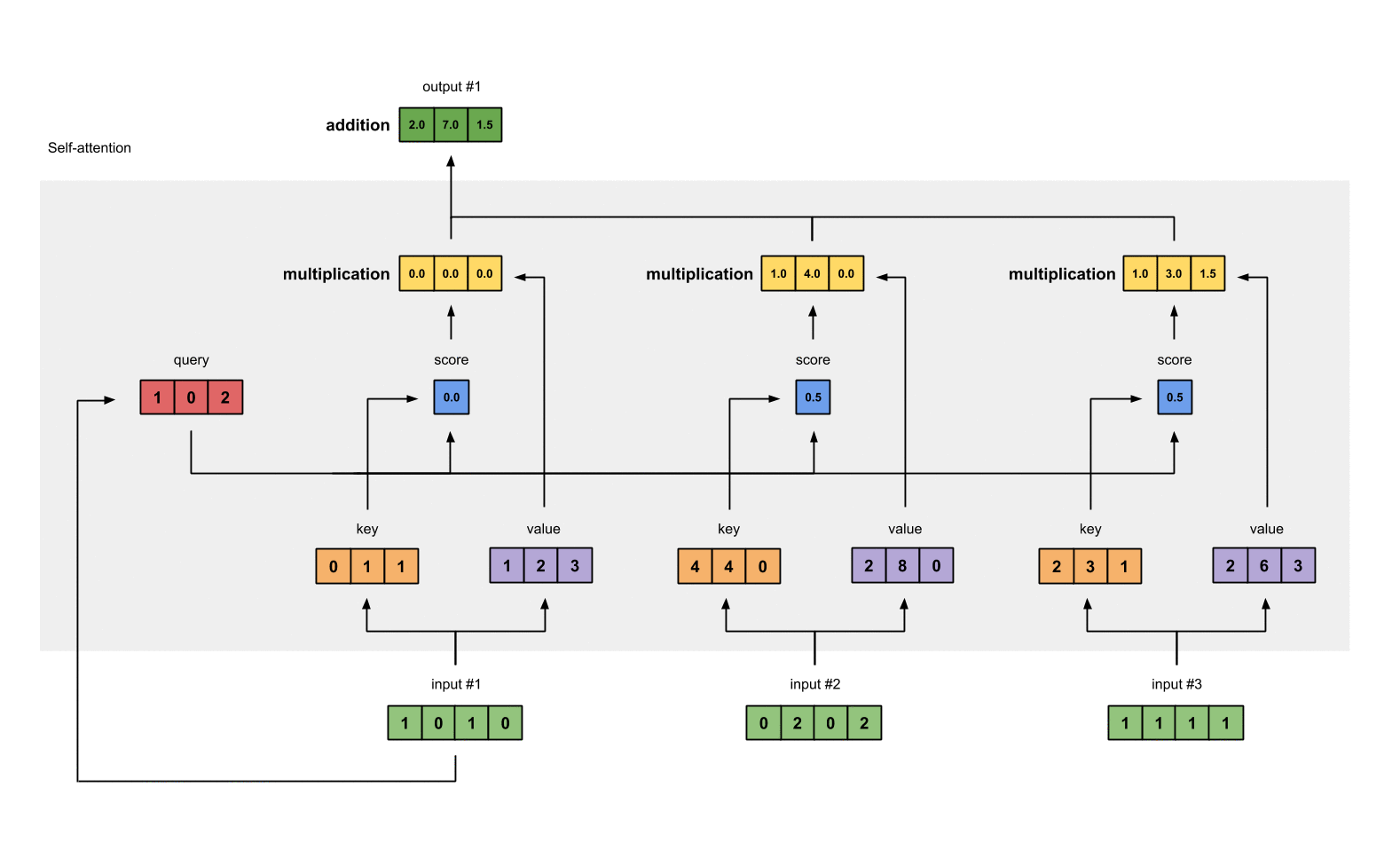
把所有的weighted values(黄色)进行element-wise的相加。
1 | [0.0, 0.0, 0.0] |
得到结果向量[2.0, 7.0, 1.5](深绿色)就是ouput1的和其他key交互的query representation。
第8步: 重复步骤4-7,获取output2,output3
现在,我们已经完成output1的全部计算,我们要对input2和input3也重复的完成步骤4~7的计算。
1 | outputs = weighted_values.sum(dim=0) |
tensorflow实现
1 | import tensorflow as tf |
transformer的三个trick
queries、keys和values
第一点就是queries、keys和values,引入可学习参数
scaling the dot product(缩放点积)
softmax功能对非常大的输入值非常敏感。这些会破坏梯度,减缓学习,或者导致学习完全停止。由于点积的平均值随着维度k而增长,因此通过下述方式有助于将点积缩小一点,以防止softmax函数的输入增长过大:
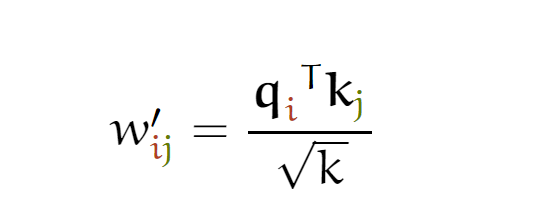
这里分母为什么要使用 根号k 呢?我们想象一下,当我们有一个所有的值都为 c 的在 ℜk 空间内的值。那它的欧式距离就为 根号kc 。除以根号k 其实就是在除以向量平均的增长长度。
这里的维度k表示为dk,其等于词向量维度/h(注意力头个数),其含义为每个注意力头需要处理的词向量维度;其实也等于这里q、k(q、k、v的size完全一致)最后一维的size。
我们上面实现self-attention时并没有加上这里的缩放操作
Multi-head attention
最后,我们必须要知道的是,在真实的语言环境中,每一个词和不同的词,都有不同的关系。我们考虑下面这个例子, I gave my dog Charlie some food 。我们可以看到 gave 和不同的部分有不同的关系。 首先, I 表示谁在进行 give 的动作, food 表达被 give 的东西是什么, Charlie 表示谁在接受东西。我们就可以用不同的Self-attention 来捕获这些不同的关系。如下图:
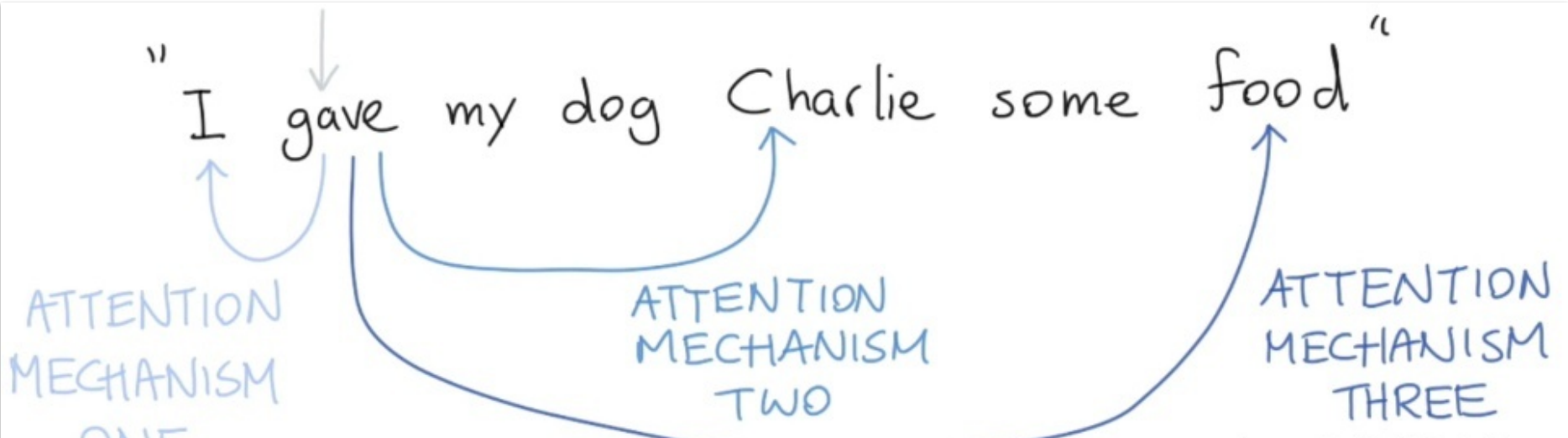
如果我们只进行一个 Self-attention,所有的信息都会被加和到一起。如果是 Charlie 给 I food ,那么我们得到的 ygave 就是一样的了,但是其实意思应发生了改变。
所以,我们可以通过增加多个 Self-attention 这样的结构,来给 self attention 更强的辨别能力,我们就有了更多个 q,k,v 的矩阵(通过给Wq、Wk、Wv增加维度),那我们把这些不同的 Self-attention 就叫做 Attention Head。有了多个 Self-attention 所代表的不同的参数,我们就可以用来表示不同的词之间的不同层面的关系了,比如说,语义层面的信息、词法方面的信息、时态方面的信息等等,这就大大的加强了 Self-attention 捕获信息的能力。