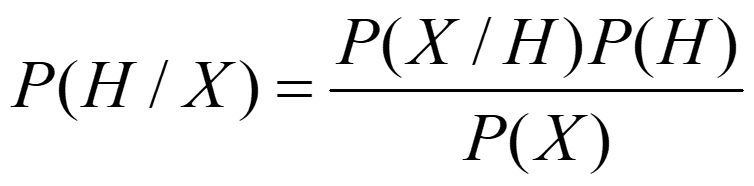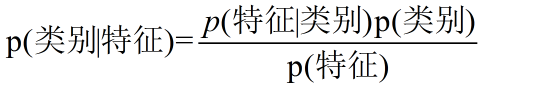记录一次程序总是异常中止的解决过程
问题描述:
开发的爬虫脚本在服务器上99%的时间都可以正常运行,但是偶尔会自动中止,进程消失。频率不固定,有的时候一天一次,有的时候一周一次,甚至很久不报错。后来解决该问题后,发现其实就是因为触发了某些条件才会出现异常,所以并不是有规律可言的。
解决过程
前面的这些解决过程不是很重要,实际是Linux系统的OOM机制导致程序被杀,不过遇到问题一般很难一开始就精准的定位到问题,都是一步步的推测问题产生的原因,然后不断地排除,直至问题的解决。所以前面这些步骤仅是在问题解决时的一些尝试性思路。